基本形式(ffundamental form)(first sencond)

公告

Posted on 2011-12-24 22:51 无忧consume 阅读(1185) 评论(0) 编辑收藏举报

第一基本形式

在微分几何中，第一基本形式（first fundamental form）是三维欧几里得空间中一个曲面的切空间中内积，由 R³ 中标准点积诱导。它使得曲面的曲率和度量性质（比如长度与面积）可与环绕空间一致地计算。第一基本形式用罗马数字 I 表示：

$\!\mathrm{I}(v,w)= \langle v,w \rangle.\,$

设 X(u, v) 是一个参数曲面，则两个切向量的内积为

$\begin{align} & {} \quad \mathrm{I}(aX_u+bX_v,cX_u+dX_v) \\ & = ac \langle X_u,X_u \rangle + (ad+bc) \langle X_u,X_v \rangle + bd \langle X_v,X_v \rangle \\ & = Eac + F(ad+bc) + Gbd, \end{align}$

这里 E, F,与 G 是第一基本形式的系数。

第一基本形式可以表示为一个对称矩阵

$\!\mathrm{I}(v,w) = v^T \begin{pmatrix} E & F \\ F & G \end{pmatrix}w.$

当第一基本形式写成一个参数时，它表示向量与自己的内积，记一步的记号

$\!\mathrm{I}(v)= \langle v,v \rangle = |v|^2.\,$

第一基本形式写成现代记法的度量张量。系数则可以写做 $g i j$ ：

$\left(g_{ij}\right) = \begin{pmatrix}g_{11} & g_{12} \\g_{21} & g_{22}\end{pmatrix} =\begin{pmatrix}E & F \\F & G\end{pmatrix}$

这个张量的分量是切向量 X₁ 与 X₂ 的数量积：

$g_{ij} = X_i \cdot X_j$

对 i, j = 1, 2。具体例子可见下一节。

计算长度与面积

第一基本形式完全描述了曲面的度量性质。从而，它使我们可以计算曲面上曲线的长度与区域的面积。线元素（line element）可以用第一基本形式的系数表示为：

$ds^2 = Edu^2+2Fdudv+Gdv^2 \,$ .

由 $dA = |X_u \times X_v| \ du\, dv$ 给出的经典面积元素可以用第一基本形式的系数利用拉格朗日恒等式（Lagrange's identity）写出，

$dA = |X_u \times X_v| \ du\, dv= \sqrt{ \langle X_u,X_u \rangle \langle X_v,X_v \rangle - \langle X_u,X_v \rangle^2 } \ du\, dv = \sqrt{EG-F^2} \, du\, dv.$

例子

R³ 中单位球面可如下参数化

$X(u,v) = \begin{pmatrix} \cos u \sin v \\ \sin u \sin v \\ \cos v \end{pmatrix},\ (u,v) \in [0,2\pi) \times [0,\pi).$

$X (u, v)$ 分别对 u 和 v 微分得出

$X_u = \begin{pmatrix} -\sin u \sin v \\ \cos u \sin v \\ 0 \end{pmatrix},\ X_v = \begin{pmatrix} \cos u \cos v \\ \sin u \cos v \\ -\sin v \end{pmatrix}.$

第一基本形式的系数可由取偏导数的点积得到：

$E = X_u \cdot X_u = \sin^2 v$ $F = X_u \cdot X_v = 0$ $G = X_v \cdot X_v = 1$

球面上曲线的长度

球面的赤道可由 $(u(t),v(t))=(t,\frac{\pi}{2})$ 参数化，这里 t 取值于 0 到 $2π$ 。线元素可用来计算这个曲线的长度。

$\int_0^{2\pi} \sqrt{ E\left(\frac{du}{dt}\right)^2 + 2F\frac{du}{dt}\frac{dv}{dt} + G\left(\frac{dv}{dt}\right)^2 } \,dt = \int_0^{2\pi} \sin v \,dt = 2\pi \sin v = 2\pi.$

球面上区域的面积

面积元素可用来计算球面的面积：

$\int_0^{\pi} \int_0^{2\pi} \sqrt{ EG-F^2 } \ du\, dv = \int_0^{\pi} \int_0^{2\pi} \sin v \, du\, dv = 2\pi \left[-\cos v\right]_0^{\pi} = 4\pi.$

高斯曲率

主条目：高斯曲率

一个曲面的高斯曲率由

$K = \frac{\det II}{\det I} = \frac{ LN-M^2}{EG-F^2 },$

给出，这里 L, M, 与 N 是第二基本形式（second fundamental form）的系数。

高斯的绝妙定理断言一个曲面的高斯曲率可以只用第一基本形式及其导数表示，从而 K 事实上是曲面的一个内蕴不变量。高斯曲率用第一基本形式明确的表达式由 Brioschi 公式给出

第二基本形式

维基百科，自由的百科全书

微分几何中，第二基本形式（second fundamental form）是三维欧几里得空间中一个光滑曲面的切丛上一个二次形式，通常记作 II。与第一基本形式一起，他们可定义曲面的外部不变量，主曲率。更一般地，若在黎曼流形中一个光滑超曲面上选取了一个光滑单位法向量场，则可定义这样一个二形式。

R³ 中曲面

R³ 中一个参数曲面 S 的第二基本形式由高斯引入。最先建设曲面是两次连续可微函数的像，z = f(x,y)，且平面 z = 0 与曲面在原点相切。则 f 以及关于 x 和 y 的偏导数在 (0,0) 皆为零。从而 f 在 (0,0) 处的泰勒展开以二次项开始：

$z=L\frac{x^2}{2} + Mxy + N\frac{y^2}{2} +$ 高阶项，

则在 (x, y) 坐标中在原点处的第二基本形式是二次型：

$L dx^2 + 2M dx dy + N dy^2. \,$

对 S 上一个光滑点 p，总可以选取坐标系使得坐标的 z-平面与 S 切于 p，然后可以相同的方式定义第二基本形式。

经典记号

一个一般参数曲面的第二基本形式定义如下。设 r=r(u,v) 是 R³ 中一个正则参数曲面，这里 r 是两个变量的光滑向量值函数。通常记 r 关于 u 和 v 的偏导数为 r_u 与 r_v。参数化的正则性意味着 r_u 与 r_v 对 r 的定义域中任何 (u,v) 是线性无关的。等价地，叉积 r_u × r_v 是曲面的一个非零法向量。参数化这样就定义了一个单位法向量场 n：

$\mathbf{n} = \frac{\mathbf{r}_u\times\mathbf{r}_v}{|\mathbf{r}_u\times\mathbf{r}_v|}.$

第二基本形式通常写成

$\mathrm{II} = Ldu^2 + 2Mdudv + Ndv^2, \,$

在基 {r_u, r_v} 下的矩阵是

$\begin{bmatrix} L&M\\ M&N \end{bmatrix}.$

在参数化 uv-平面上一个给定点处系数 L, M, N 由 r 在那个点的二次偏导数到 S 的法线上投影给出，利用点积可计算如下：

$L = \mathbf{r}_{uu} \cdot \mathbf{n}, \quad M = \mathbf{r}_{uv} \cdot \mathbf{n}, \quad N = \mathbf{r}_{vv} \cdot \mathbf{n}.$

现代记法

一个通常曲面 S 的第二基本形式定义如下：设 r=r(u¹,u²) 是 R³ 中一个正则参数曲面，这里 r 是两个变量的光滑向量值函数。通常记 r 关于 u^α 的偏导数为 r_α，α = 1，2。参数化的正则性意味着 r₁ 与 r₂ 在 r 的定义域上是线性无关的，从而在每一点张成 S 的切空间。等价地，叉积 r₁ × r₂ 是曲面的一个非零法向量。这样参数化定义了一个单位法向量场 n：

$\mathbf{n} = \frac{\mathbf{r}_1\times\mathbf{r}_2}{|\mathbf{r}_1\times\mathbf{r}_2|}.$

第二基本形式通常写作

$\mathrm{II} = b_{\alpha, \beta} du^{\alpha} du^{\beta}. \,$

上式使用了爱因斯坦求和约定。

在参数 (u¹, u²)-曲面给定点处系数 b_α,β 由 r 的二次偏导数到 S 的法线的投影给出，利用点积可写成：

$b_{\alpha, \beta} = \mathbf{r}_{\alpha, \beta} \cdot \mathbf{n}.$

黎曼流形中的超曲面

在欧几里得空间中，第二基本形式由

$I\!I(v,w) = \langle d\nu(v),w\rangle$

给出，这里 $ν$ 是高斯映射，而 $d ν$ 是 $ν$ 的微分视为一个向量值微分形式，括号表示欧几里得空间的度量张量。

更一般地，在一个黎曼流形上，第二基本形式是描述一个超曲面形算子（记作 S）的等价方法，

$\mathrm I\!\mathrm I(v,w)=\langle S(v),w\rangle= -\langle \nabla_v n,w\rangle=\langle n,\nabla_v w\rangle,$

这里 $\nabla_v w$ 表示周围空间的共变导数，n 超曲面上一个法向量场。如果仿射联络是无挠的，则第二基本形式是对称的。

第二基本形式的符号取决于 n 的方向的选取。（这称为曲面的余定向，对欧几里得空间中的曲面，等价于给定曲面的一个定向）。

推广为任意余维数

第二基本形式可以推广到任意余维数。在这种情形下，它是切空间上取值于法丛的一个二次型，可以定义为

$\mathrm{I}\!\mathrm{I}(v,w)=(\nabla_v w)^\bot,$

这里 $(\nabla_v w)^\bot$ 表示共变导数 $\nabla_v w$ 到法丛的正交投影。

在欧几里得空间中，子流形的曲率张量可以描述为下列公式：

$\langle R(u,v)w,z\rangle =\langle \mathrm I\!\mathrm I(u,z),\mathrm I\!\mathrm I(v,w)\rangle-\langle \mathrm I\!\mathrm I(u,w),\mathrm I\!\mathrm I(v,z)\rangle.$

这叫做高斯方程，可以视为高斯绝妙定理的推广。在一个标准正交基中第二基本形式的本征值，是曲面的主曲率。一组正交规范本征向量称为主方向。

对一般的黎曼流形必须添加周围空间的曲率；如果 N 是嵌入黎曼流形 (M,g) 中一个流形，则 N 在诱导度量下的曲率张量 $R N$ 可以用第二基本形式与 M 的曲率张量 $R M$ 表示出来：

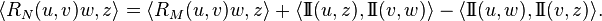
$\langle R_N(u,v)w,z\rangle = \langle R_M(u,v)w,z\rangle+\langle \mathrm I\!\mathrm I(u,z),\mathrm I\!\mathrm I(v,w)\rangle-\langle \mathrm I\!\mathrm I(u,w),\mathrm I\!\mathrm I(v,z)\rangle.$

刷新页面返回顶部