差分,又名差分函数或差分运算,是数学中的一个概念。它将原函数  映射到
映射到  。差分运算,相应于微分运算,是微积分中重要的一个概念。
。差分运算,相应于微分运算,是微积分中重要的一个概念。
前向差分差分的定义分为前向差分和逆向差分两种。
函数的前向差分通常简称为函数的差分。对于函数 ,如果:
,如果:
 ,
,
则称 为
为 的一阶前向差分。在微积分学中的有限差分(finite differences),前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当
的一阶前向差分。在微积分学中的有限差分(finite differences),前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当 是多项式时,前向差分为Delta算子,一种线性算子。前向差分会将多项式阶数降低1。
是多项式时,前向差分为Delta算子,一种线性算子。前向差分会将多项式阶数降低1。
逆向差分
对于函数 ,如果:
,如果:
则称 为
为 的一阶逆向差分。
的一阶逆向差分。
差分的阶
称](http://upload.wikimedia.org/wikipedia/zh/math/4/4/8/4489c55ea2dc6cdfccc9fd68236b9245.png) 为
为 的
的 阶差分,即
阶差分,即 前向阶差分 ,如果
前向阶差分 ,如果
根据数学归纳法,有
其中,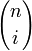 为二项式系数。
为二项式系数。
特别的,有
差分的性质
- 如果C为常数,则有
- 线性:如果
 和
和  为常数,则有
为常数,则有
- 乘法定则:
- 除法定则:

- 或


- 级数:
牛顿数列
牛顿数列(级数),也称作牛顿前向差分方程是一个以数学与物理学家牛顿命名的函数关系。具体为:
要注意的是,上式对所有的多项式都成立,但只对部分解析函数成立。其中
为二项式系数,
为  的
的 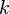 阶下降阶乘幂。牛顿数列与泰勒级数的相似性是哑微积分的一个典型。
阶下降阶乘幂。牛顿数列与泰勒级数的相似性是哑微积分的一个典型。
卡尔森定理(Carlson's theorem)指出,如果一个函数的牛顿数列存在,则该函数存在的牛顿数列是唯一的。然而牛顿数列并不总存在。
牛顿数列是差分多项式(差分级数)的特例。


 \}](http://upload.wikimedia.org/wikipedia/zh/math/8/a/f/8af2e27c3325ced0ee6c4367598d30f2.png)
 - \Delta^{n-1} [f](x)](http://upload.wikimedia.org/wikipedia/zh/math/4/e/1/4e1705339fb621144663fa7c4cf5ec3b.png)
 = \sum_{i=0}^n {n \choose i} (-1)^{n-i} f(x+i)](http://upload.wikimedia.org/wikipedia/zh/math/f/7/3/f73c2538a807ad90c99520dad7e7d96c.png)
 = f(x+2) - 2f(x+1) + f(x)](http://upload.wikimedia.org/wikipedia/zh/math/3/5/7/357e3845eb0e6fb8eb47755085f69cce.png)






}{k!}(x)_k
= \sum_{k=0}^\infty {x \choose k} \Delta^k [f](a)](http://upload.wikimedia.org/wikipedia/zh/math/6/f/a/6fa6d5dce3a3416d1792adaeefdf376a.png)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号