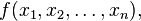海森矩阵(Hessian matrix 或 Hessian)

公告

Posted on 2011-12-20 20:50 无忧consume 阅读(1440) 评论(0) 编辑收藏举报

在数学中，海森矩阵（Hessian matrix 或 Hessian）是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵，此函数如下：

$f(x_1, x_2, \dots, x_n),$

如果 f 所有的二阶导数都存在，那么 f 的海森矩阵即：

H (f) i j (x) = D i D j f (x)

其中 $x = (x_1, x_2, \dots, x_n)$ ，即

$H(f) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\,\partial x_n} \\ \\ \frac{\partial^2 f}{\partial x_2\,\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\,\partial x_n} \\ \\ \vdots & \vdots & \ddots & \vdots \\ \\ \frac{\partial^2 f}{\partial x_n\,\partial x_1} & \frac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}$

（也有人把海森定义为以上矩阵的行列式）海森矩阵被应用于牛顿法解决的大规模优化问题。

混合偏导数和海森矩阵的对称性

海森矩阵的混合偏导数是海森矩阵非主对角线上的元素。假如他们是连续的，那么求导顺序没有区别，即

$\frac {\partial}{\partial x} \left( \frac { \partial f }{ \partial y} \right) = \frac {\partial}{\partial y} \left( \frac { \partial f }{ \partial x} \right)$

上式也可写为

$f_{xy} = f_{yx} \,$

在正式写法中，如果 f 函数在区域 D 内连续并处处存在二阶导数，那么 f的海森矩阵在 D 区域内为对称矩阵。

在 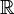$\mathbb{R}^2$ → $\mathbb{R}$ 的函数的应用

给定二阶导数连续的函数 $f: \mathbb{R}^2 \to \mathbb{R}$ ，海森矩阵的行列式，可用于分辨 $f$ 的临界点是属于鞍点还是极值点。

对于 $f$ 的临界点 $(x 0, y 0)$ 一点，有 $\frac{\partial f(x_0, y_0)}{\partial x} = \frac{\partial f(x_0, y_0)}{\partial y} = 0$ ，然而凭一阶导数不能判断它是鞍点、局部极大点还是局部极小点。海森矩阵可能解答这个问题。

$H = \begin{vmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x\,\partial y} \\ \\ \frac{\partial^2 f}{\partial y\,\partial x} & \frac{\partial^2 f}{\partial y^2} \end{vmatrix} = \frac{\partial^2 f}{\partial x^2} \frac{\partial^2 f}{\partial y^2} - (\frac{\partial^2 f}{\partial y\,\partial x})^2$

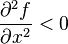H > 0 ：若 $\frac{\partial^2 f}{\partial x^2} > 0$ ，则 $(x 0, y 0)$ 是局部极小点；若 $\frac{\partial^2 f}{\partial x^2} < 0$ ，则 $(x 0, y 0)$ 是局部极大点。
H < 0 ： $(x 0, y 0)$ 是鞍点。
H = 0 ：二阶导数无法判断该临界点的性质，得从更高阶的导数以泰勒公式考虑。

刷新页面返回顶部

无忧consume

公告