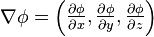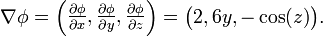公告

梯度

Posted on 2011-12-20 20:05 无忧consume 阅读(2183) 评论(0) 编辑收藏举报

梯度

在向量微积分中，标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。更严格的说，从欧几里得空间Rⁿ到R的函数的梯度是在Rⁿ某一点最佳的线性近似。在这个意义上，梯度是雅可比矩阵的一个特殊情况。

上面两个图中，标量场是黑白的，黑色表示大的数值，而其相应的梯度用蓝色箭头表示。

在单变量的实值函数的情况，梯度只是导数，或者，对于一个线性函数，也就是线的斜率。

梯度一词有时用于斜度，也就是一个曲面沿着给定方向的倾斜程度。可以通过取向量梯度和所研究的方向的点积来得到斜度。梯度的数值有时也被称为梯度。

梯度的解释

假设有一个房间，房间内所有点的温度由一个标量场 $ϕ$ 给出的，即点 $(x, y, z)$ 的温度是 $ϕ(x, y, z)$ 。假设温度不随时间改变。然后，在房间的每一点，该点的梯度将显示变热最快的方向。梯度的大小将表示在该方向上变热的速度。

考虑一座高度在 $(x, y)$ 点是 $H (x, y)$ 的山。 $H$ 在一点的梯度是在该点坡度（或者说斜度）最陡的方向。梯度的大小告诉我们坡度到底有多陡。

梯度也可以告诉我们一个数量在不是最快变化方向的其他方向的变化速度。再次考虑山坡的例子。可以有条直接上山的路其坡度是最大的，则其坡度是梯度的大小。也可以有一条和上坡方向成一个角度的路，例如投影在水平面上是60°角。则，若最陡的坡度是40%，这条路的坡度小一点，是20%，也就是40%乘以60°的余弦。

这个现象可以如下数学的表示。山的高度函数 $H$ 的梯度点积一个单位向量给出了表面在该向量的方向上的斜率。这称为方向导数。

形式化定义

一个标量函数 $φ$ 的梯度记为：

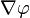$\nabla \varphi$ 或

gradφ

其中 $\nabla$ （nabla）表示向量微分算子。

在三维情况，该表达式在直角坐标中扩展为

$\nabla \phi =\begin{pmatrix} {\frac{\partial \phi}{\partial x}}, {\frac{\partial \phi}{\partial y}}, {\frac{\partial \phi}{\partial z}} \end{pmatrix}$

（参看偏导数和向量。）

虽然使用坐标表达，但结果是在正交变换下不变，从几何的观点来看，这是应该的。

范例

函数 $φ = 2 x + 3 y 2 - sin(z)$ 的梯度为：

$\nabla \phi = \begin{pmatrix} {\frac{\partial \phi}{\partial x}}, {\frac{\partial \phi}{\partial y}}, {\frac{\partial \phi}{\partial z}} \end{pmatrix} = \begin{pmatrix} {2}, {6y}, {-\cos(z)} \end{pmatrix}.$

流形上的梯度

一个黎曼流形M上的对于任意可微函数，f的梯度是一个向量场使得对于每个向量 $ξ$ ，

$\langle \nabla f(x), \xi \rangle := \xi f$

其中 $\langle \cdot, \cdot \rangle$ 代表M上的内积（度量）而 $ξ f$ 是在p点取任意点映射到在 $ξ$ 的方向导数的函数。换句话说，在某些坐标图中 $φ$ , $ξ f (p)$ 将成为：

$\sum \xi_{x_{j}} (\partial_{j}f \mid_{p}) := \sum \xi_{x_{j}} (\frac{\partial}{\partial x_{j} }(f \circ \varphi^{-1}) \mid_{\varphi(p)}).$

函数的梯度和外微分相关，因为 $ξ f (p) = d f (ξ)$ 。实际上度量容许我们可以用一种标准的方式将1-形式df和向量场 $\nabla f$ 建立联系，这样梯度可以等同于0-形式的外微分。

柱坐标下的梯度（ $\nabla$ ）算符

$\nabla f(\rho,\theta,z) = \frac{\partial f}{\partial\rho} \mathbf{e}_{\rho} + \frac1{\rho}\frac{\partial f}{\partial\theta} \mathbf{e}_{\theta} + \frac{\partial f}{\partial z} \mathbf{e}_{z}$

球坐标下的梯度（ $\nabla$ ）算符

$\nabla f(r,\theta,\phi) = \frac{\partial f}{\partial r} \mathbf{e}_{r} + \frac1{r}\frac{\partial f}{\partial\theta} \mathbf{e}_{\theta} + \frac1{r\sin \theta}\frac{\partial f}{\partial \phi} \mathbf{e}_{\phi}$

其中 $θ$ 为极角， $ϕ$ 方位角。

刷新页面返回顶部

无忧consume

公告

梯度

梯度

梯度的解释

形式化定义

范例

流形上的梯度

柱坐标下的梯度（）算符

球坐标下的梯度（）算符

柱坐标下的梯度（ $\nabla$ ）算符

球坐标下的梯度（ $\nabla$ ）算符