欧拉－拉格朗日方程

Posted on 2011-12-18 23:57  无忧consume  阅读(1204)  评论(0)  编辑  收藏  举报

欧拉－拉格朗日方程 

欧拉-拉格朗日方程 (Euler-Lagrange equation) 为变分法中的一条重要方程。它提供了求泛函的平稳值的一个方法。

设 f=f(x,\ y,\ z) ，以及 f_y,\ f_z 在 [a,\ b]\times\mathbb{R}^2 中连续，并设泛函第一方程

J(y)=\int_a^b f(x, y(x), y'(x))dx 。

若 y\in C^1[a,\ b] 使得泛函 J(y) 取得局部平稳值，则对于所有的 x\in(a,\ b) ，

\frac{d}{dx}\frac{\partial}{\partial y'}f(x, y, y')=\frac{\partial}{\partial y}f(x, y, y') 。

推广到多维的情况， 记

\vec{y}(x)=(y_1(x), y_2(x), \ldots, y_n(x)) ，
\vec{y}'(x)=(y'_1(x), y'_2(x), \ldots, y'_n(x)) ，
f(x, \vec{y}, \vec{y}')=f(x, y_1(x), y_2(x), \ldots, y_n(x), y'_1(x), y'_2(x), \ldots, y'_n(x)) 。

若 \vec{y}'(x)\in(C^1[a, b])^n 使得泛函  J(\vec{y})=\int_a^bf(x, \vec{y}, \vec{y}')dx 取得局部平稳值，则在区间 (a,\ b) 内对于所有的  i=1,\ 2,\ \ldots,\ n ，皆有

\frac{d}{dx}\frac{\partial}{\partial y'_i}f(x, \vec{y}, \vec{y}')=\frac{\partial}{\partial y_i}f(x, \vec{y}, \vec{y}') 。

第二方程

设 f=f(x,\ y,\ z) ，及 f_y,\ f_z 在 [a,\ b]\times\mathbb{R}^2 中连续，若 y\in C^1[a,\ b] 使得泛函 J(y)=\int_a^b f(x, y(x), y'(x))dx 取得局部平稳值，则存在一常数 C ，使得

f(x, y, y')-y'(x)f_{y\,'}(x, y, y')=\int_a^x f_x(x(t), y(t), y'(t))dt+C 。

例子

设 (0,\ 0) 及 (a,\ b) 为直角坐标上的两个固定点，欲求连接两点之间的最短曲线。设 (x(t),\ y(t)) (t\in[0,\ 1]) ，并且

(x(0),\ y(0))=(0,\ 0),\ (x(1),\ y(1))=(a,\ b) ；

这里，(x(t),\ y(t))\in C^1[0,\ 1] 为连接两点之间的曲线。则曲线的弧长为

L(y)=\int_0^1\sqrt{[x'(t)]^2+[y'(t)]^2}dt 。

现设

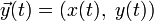\vec{y}(t)=(x(t),\ y(t)) ，
f(t,\ \vec{y}(t),\ \vec{y}'(t))=\sqrt{x'(t)^2+y'(t)^2} ，

取偏微分，则

f_{x'}=\frac{x'(t)}{\sqrt{x'(t)^2+y'(t)^2}} ，
f_{y'}=\frac{y'(t)}{\sqrt{x'(t)^2+y'(t)^2}} ，
fx = fy = 0 。

若 y 使得 L(y) 取得局部平稳值，则 y 符合第一方程：

\frac{d}{dt}f_{x'}(t, y, y')=f_x(t, y, y')=0 ，
\frac{d}{dt}f_{y'}(t, y, y')=f_y(t, y, y')=0 。

因此，

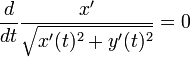\frac{d}{dt}\frac{x'}{\sqrt{x'(t)^2+y'(t)^2}}=0 ，
\frac{d}{dt}\frac{y'}{\sqrt{x'(t)^2+y'(t)^2}}=0 。

随 t 积分，

\frac{x'}{\sqrt{x'^2+y'^2}}=C_0 ，
\frac{y'}{\sqrt{x'^2+y'^2}}=C_1 ；

这里，C_0,\ C_1 为常数。重新编排，

x'=\sqrt{\frac{C_0^2}{1-C_0^2}}=r ，
y'=\sqrt{\frac{C_1^2}{1-C_1^2}}=s 。

再积分，

x(t) = rt + r' ，
y(t) = st + s' 。

代入初始条件

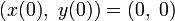(x(0),\ y(0))=(0,\ 0) ，
(x(1),\ y(1))=(a,\ b) ；

即可解得 (x(t),\ y(t))=(at,\ bt) ，是连接两点的一条线段。

另经过其他的分析，可知此解为唯一解，并且该解使得 L(y) 取得极小值，所以在平面上连结两点间弧长最小的曲线为一直线。

参阅

Copyright © 2024 无忧consume
Powered by .NET 8.0 on Kubernetes