高斯散度定理
更加精确地说,高斯公式说明向量场穿过曲面的通量,等于曲面内部区域的散度的三重积分。直观地,所有源点的和减去所有汇点的和,就是流出一个区域的流量。
高斯公式在工程数学中是一个很重要的结果,特别是静电学和流体力学。
设空间闭区域Ω是由分片光滑的闭曲面Σ所围成,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数,则有定理
或
这里Σ是Ω的整个边界曲面的外侧,cos α、cos β、cos γ是Σ在点(x,y,z)处的法向量的方向余弦
这两个公式叫做高斯公式。
用散度表示
高斯公式用散度表示为:
其中Σ是空间闭区域Ω的边界曲面,而
n是向量A在曲面Σ的外侧法向量上的投影。
用向量表示
令V代表有一间单闭曲面S为边界的体积, 是定义在V中和S上连续可微的矢量场。如果
是定义在V中和S上连续可微的矢量场。如果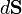 是外法向矢量面元,则
是外法向矢量面元,则
推论
- 对于标量函数g和向量场F的积,应用高斯公式可得:
- 对于两个向量场
 的向量积,应用高斯公式可得:
的向量积,应用高斯公式可得:
- 对于标量函数f和非零常向量的积,应用高斯公式可得:
- 对于向量场F和非零常向量的向量积,应用高斯公式可得:
例子
假设我们想要计算
其中S是由x2 + y2 + z2 = 1所定义的单位球,F是向量场
直接计算这个积分是相当困难的,但我们可以用高斯公式来把它简化:
由于函数y和z是奇函数,我们有:
因此:
二阶张量的高斯公式
二阶张量的高斯公式实际上是上面的高斯公式的推论。为了使内容完整,首先简要地介绍三维欧几里得空间上的二阶张量(详见并矢张量或张量积)以及相关的概念和记号。在这里,矢量和矢量场用黑斜体字母表示,张量用正黑体字母表示。
- 两个矢量
 和
和 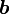 并排放在一起所形成的量
并排放在一起所形成的量  被称为矢量
被称为矢量  和
和 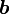 的并矢或并矢张量。要注意,一般来说,
的并矢或并矢张量。要注意,一般来说, 。
。  的充分必要条件是
的充分必要条件是 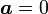 或
或  。
。- 二阶张量就是有限个并矢的线性组合。
 分别线性地依赖于
分别线性地依赖于  和
和 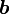 。
。- 二阶张量
 和矢量
和矢量  的缩并
的缩并  以及
以及  对
对  和
和  都是线性的。
都是线性的。 - 特别是,当
 时,
时,
所以,一般说来, 。
。
下面举一个例子:用二阶张量及其与矢量的缩并来重新写  和
和 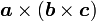 。
。
我们还用到二阶张量  的转置
的转置  (又可以记为
(又可以记为  ),定义如下:
),定义如下:
 仍然是一个二阶张量,并且线性地依赖于
仍然是一个二阶张量,并且线性地依赖于  。
。 。
。
定理: 设 V 是三维欧几里得空间中的一个有限区域,S 是它的边界曲面,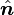 是 S 的外法线方向上的单位矢量,
是 S 的外法线方向上的单位矢量, 是定义在 V 的某个开邻域上的 C1 连续的二阶张量场,
是定义在 V 的某个开邻域上的 C1 连续的二阶张量场, 是
是  的转置,则
的转置,则
证明:下面以第二个式子为例进行证明。令第二个式子的左边为  ,则
,则
接下来利用矢量场的高斯公式,可得
于是
至此证毕。






















 浙公网安备 33010602011771号
浙公网安备 33010602011771号