计算机中神奇的补码

补码

1. 用二进制表示正数或负数

任何一个\(10\)进制数，都可以转化为\(2\)进制数，并且只需要增加一个符号位\(0/1\)就可以描述数的正负了。

如 \((2)_{10} = (010)_{2} , (-2)_{10}=(110)_2\)

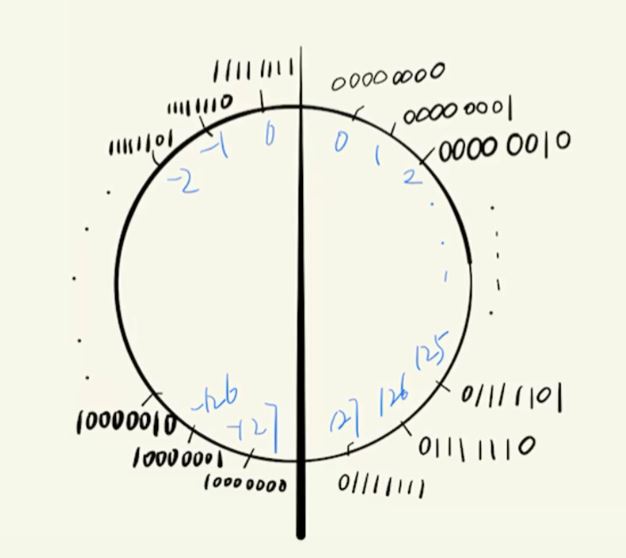
如果给输入的数据加入大概的范围，如\([-127,128]\)，那么可以估算出所需要的符号位数\(n = 8\)

那么\((2)_{10} = (00000010)_{2} , (-2)_{10}=(10000010)_2\)。

2. 用二进制数表示正数+负数

显然\((2)_{10} + (-2)_{10} = (00000010)_{2} + (10000010)_2 \ne (0)_2\)，那么原来的二进制编码方法就无法胜任这个工作。

那么如何让正数+负数可以满足可加性呢？

一个很显然的想法，正数的不变，负数符号位不变，其他位置取反就行了。

\((2)_{10} + (-2)_{10} = (00000010)_{2} + (11111101)_2 = (00000000)_2\)（舍去最后进位的最高位）

但是\((11111111)_2 = (00000000)_2 = (0)_{10}\)，就导致了\(0\)的二进制编码不唯一，就会造成一定的不便。

3. 同时将一个十进制数只对应一个二进制编码

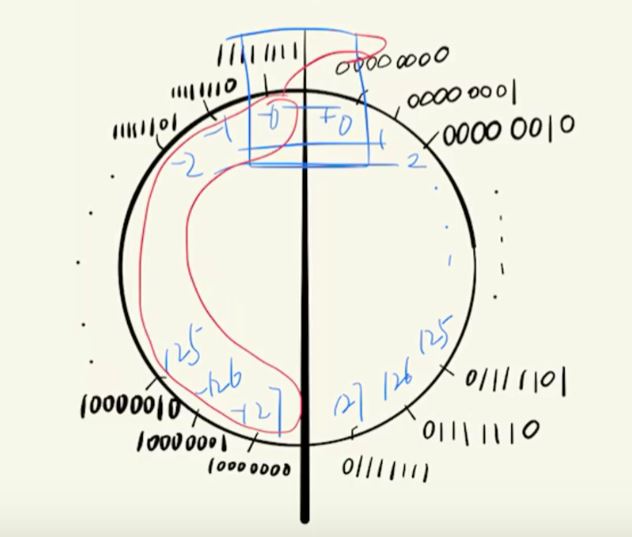
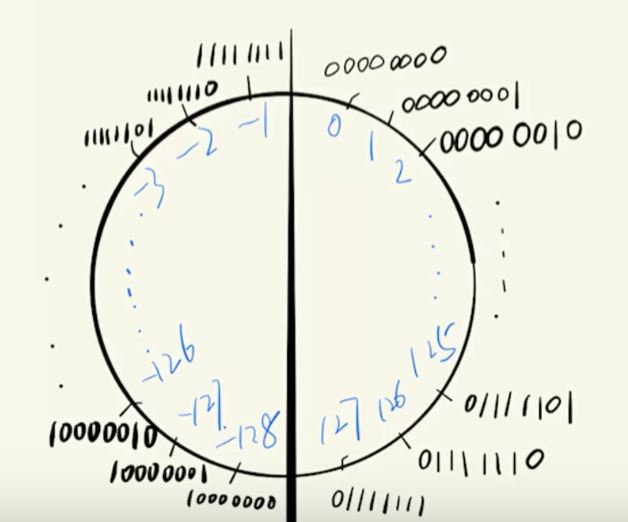
一个显然的想法就是把\((11111111)_2\)合并到 \((00000000)_2\)中去，其他的负数顺次移动\(1\)个单位，剩下的一个数\((10000000)_2\)对应十进制数\(-128\)而没有一个二进制数\(+128\)与之对应。

4. 补码的计算方法

上图可以知道，非负数原码和补码一致，而负数原码到补码就是取反顺时针移动一个单位。

设要求二进制数\(x\)（正数或者负数）的补码：

• 若\(x\geq 0\)那么，其补码就是\(x\).
• 若\(x < 0\) 那么，其补码就是\(\overline{x} + 1\).