第三次作业
作业要求
题目:最大连续子数组和(最大子段和)
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
过程
- 环境
这次使用的化境为vs2017,环境界面如下:
- 算法
使用的算法为材料中给的第三种算法,进行本地移植后,代码如下:
int zuida::tmain(int A[], int n)
{
int c = 0;//用于标识有没有正数
int array_length = n;//数组大小
int maxSum = A[0];//记录最大子数组的和
for (int i = 0; i < array_length - 1; i++)
{
int sum = 0;
if (A[i] >= 0)
{
c = 1;//当数组中出现正数时标识位置1
}
//寻找以A[i+1]为终点的最大子数组
for (int j = i + 1; j >= 0; j--)
{
sum += A[j];
if (sum > maxSum)
{
maxSum = sum;
}
}
}
if (c == 1)//判断数组中是否为全负数
{
return maxSum;//将结果返回
}
else
return 0;//当全为负数时,输返回0
}
- 单元测试
- 单元测试方式有:
(1)语句覆盖:使得程序中每个语句至少都能被执行一次。
(2)判定覆盖:使得程序中每个判定至少为T和F各一次。
(3)条件覆盖:使得判定中的每个条件获得各种可能的结果。
(4)判定/条件覆盖:同时满足判定覆盖和条件覆盖。
(5)条件组合覆盖:使得每个判定中条件的各种可能组合都至少出现一次。
我选择的是判定条件覆盖。
(1)sum>num sum>=0
(2)sum>num sum<0
(3)sum>num sum>=0
(4)sum<num sum<0 - 测试用例:
(1){1,2,3,4,5}
(2){-1,-2,-3,-4,-5}
(3){1,-2,3,-4,5}
(4){-6, 10, -5, 6, -7} - 测试代码:
namespace UnitTest1
{
TEST_CLASS(UnitTest1)
{
public:
TEST_METHOD(TestMethod1)
{
// TODO: 在此输入测试代码
zuida c;
int n = 5;
int a[5] = { 1,2,3,4,5 };//全正测试
int s = 15;
int d = c.tmain(a, n);
Assert::AreEqual(s, d);
}
TEST_METHOD(TestMethod2)
{
// TODO: 在此输入测试代码
zuida c;
int n = 5;
int a[5] = { -1,-2,-3,-4,-5 };//全负测试
int s = 0;
int d = c.tmain(a, n);
Assert::AreEqual(s, d);
}
TEST_METHOD(TestMethod3)
{
// TODO: 在此输入测试代码
zuida c;
int n = 5;
int a[5] = { 1,-2,3,-4,5 };//正负交替测试
int s = 5;
int d = c.tmain(a, n);
Assert::AreEqual(s, d);
}
TEST_METHOD(TestMethod4)
{
// TODO: 在此输入测试代码
zuida c;
int n = 5;
int a[5] = { -6, 10, -5, 6, -7 };
int s = 11;
int d = c.tmain(a, n);
Assert::AreEqual(s, d);
}
};
}
- 测试结果
创建一个单元测试:
将代码写入,执行单元测试:
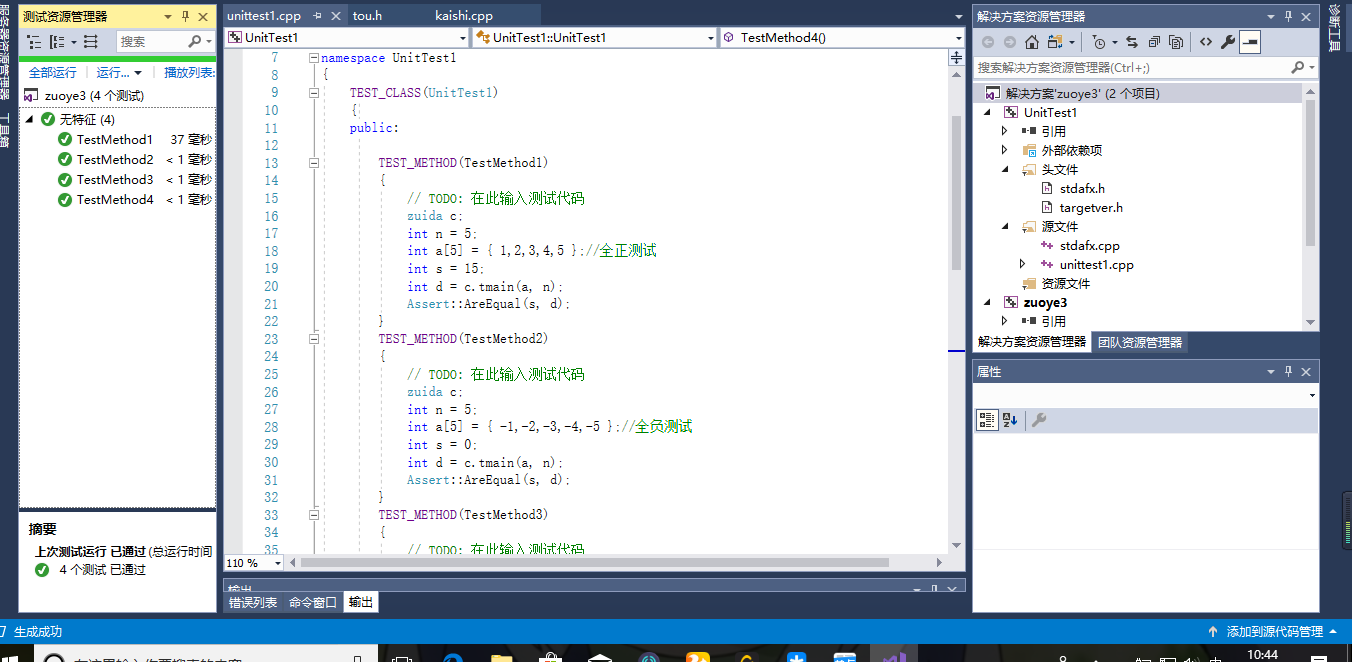
运行成功!
总结
这次作业,让我深刻的了解了单元测试,对于环境的运用,也熟练了许多。这次的单元测试代码为自己编写,这在上一次作业是不存在的,这证明了我有了一定的成长。不过这次作业的核心算法依然为老师提供,我只是做了一下简单的本地移植,希望在下次作业可以做到独立完成!






