PyTorch之线性回归模型
1 简介
1.1 线性回归模型简介
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = wx+e,e为误差服从均值为0的正态分布。其中只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,称为一元线性回归。
1.2 Tensor
PyTorch 是一个开源的 Python 机器学习库,基于 Torch。其中Tensor是深度学习中最为基础也最为关键的数据结构:
- Tensor之于PyTorch就好比是array之于Numpy或者DataFrame之于Pandas,都是构建了整个框架中最为底层的数据结构;
- Tensor与普通的数据结构不同,具有一个极为关键的特性——自动求导。
其中Numpy很容易转化成Tensor,参考方式:
import numpy as np
import torch
a = np.random.normal(0, 1, (2, 3))
# 使用torch.tensor
b = torch.tensor(a)
# 使用torch.from_numpy
b = torch.from_numpy(a)
2. 数据准备
2.1 数据集概述
在这个示例中,我们将使用一个虚构的数据集,该数据集包含房屋面积和价格的信息。我们的目标是通过面积来预测房价,这是一个典型的线性回归问题。
import torch
import torch.nn as nn
# 房屋面积,设置为浮点型
areas = torch.arange(20.0, 40.0)
# 房价
prices = torch.tensor([5*areas[i]+random.randint(-5,5) for i in range(len(areas))])
2.2 数据直观分析
Matplotlib 是 Python 生态系统的一个重要组成部分,是用于可视化的绘图库。拿到数据先绘图看下分布情况,参考代码如下:
import matplotlib.pyplot as plt
plt.xlabel("areas")
plt.ylabel("prices")
plt.scatter(areas,prices)
plt.show()
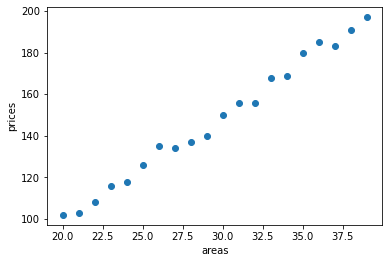
初步判定虚拟数据集符合此次实验要求
3 PyTorth实现线性回归
3.1 认识Linear
nn.Linear 是 PyTorch 中用于创建线性层的类,官方定义如下:
class torch.nn.Linear(in_features, out_features, bias=True)
对输入数据做线性变换:y=Ax+b
变量:
- weight -形状为(out_features x in_features)的模块中可学习的权值
- bias -形状为(out_features)的模块中可学习的偏置
3.2 构建模型
class LinearRegressionModel(nn.Module):
def __init__(self):
super(LinearRegressionModel, self).__init__()
# 输入和输出的维度都是1
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
3.3 选择损失函数和优化器
我们使用均方误差作为损失函数,使用随机梯度下降作为优化器。
model = LinearRegressionModel()
# 选择损失函数
criterion = nn.MSELoss()
# 选择优化器
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
3.4 数据标准化/规范化
在PyTorch中,通过对输入数据进行标准化处理,可以使输入数据的分布更加均匀,减少模型训练过程中的不稳定性,提高模型的泛化能力。常见的方法有:
- 最大值标准化
- 绝对最大值标准化
- 最大最小值标准化
- 均值方差标准化
- 范数标准化
- 四分位法标准化
这个场景我们选择均值方差标准化,对数据进行标准化处理:
class DataNormal:
def __init__(self, arr):
self.arr = arr
self.mean = torch.mean(self.arr)
self.std = torch.std(self.arr)
def encode(self, v):
return (v - self.mean) / self.std
def decode(self, v):
return v * self.std + self.mean
# 初始化标准化类,后续预测也会用到
dn_areas = DataNormal(areas)
dn_prices = DataNormal(prices)
# 输入数据标准化
x = dn_areas.encode(areas)
y = dn_prices.encode(prices)
3.5 模型训练
# 转换为二维张量
inputs = x.view(-1,1)
targets = y.view(-1,1)
# 进行 100 轮训练
for epoch in range(100):
# 前向传播
outputs = model(inputs)
loss = criterion(outputs, targets)
# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
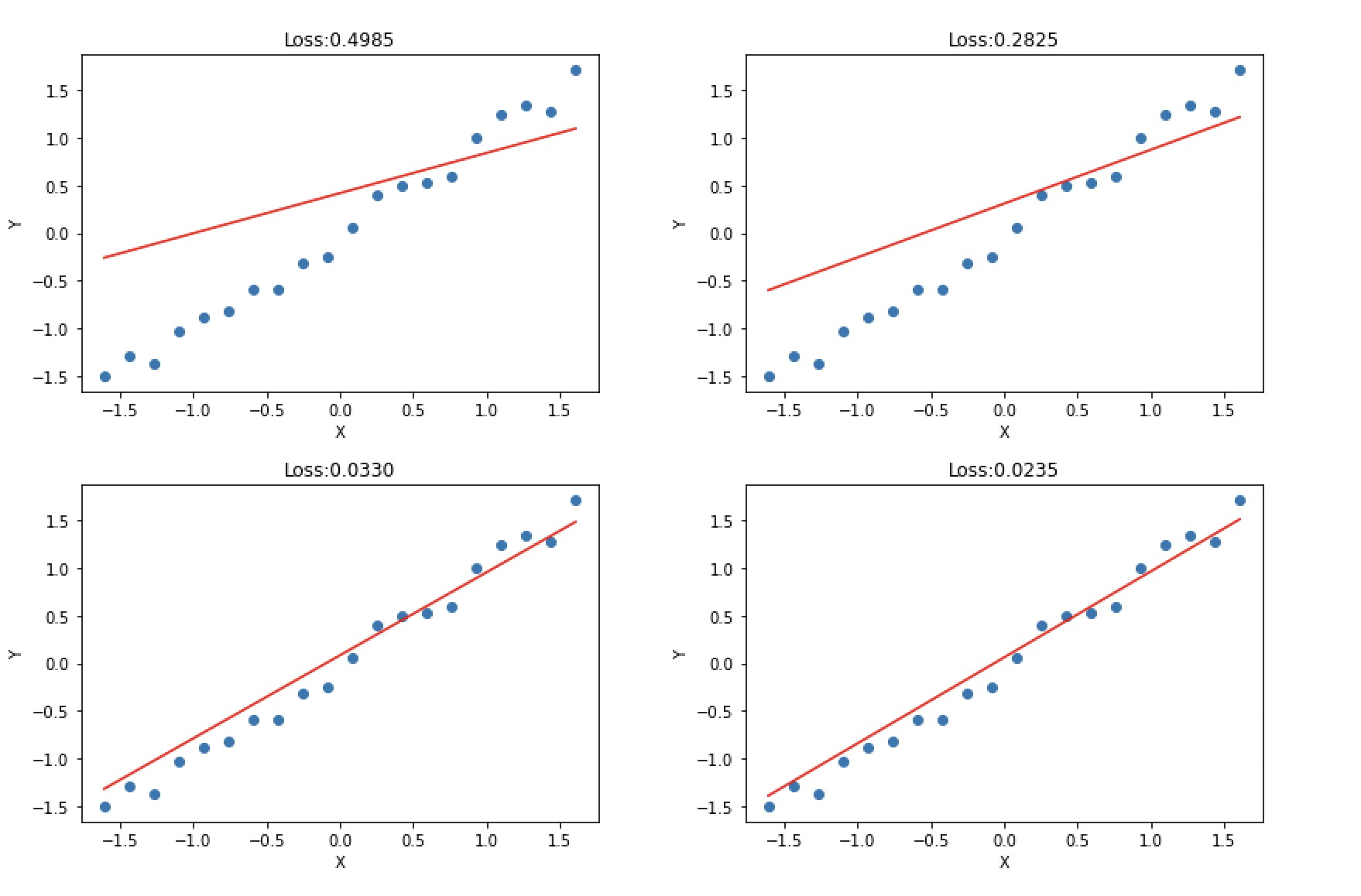
# 效果可视化,非必需
if epoch % 5 == 0:
predict = model(inputs)
plt.plot(x.data.numpy(),predict.squeeze(1).data.numpy(),"r")
loss = criterion(predict,targets)
plt.title("Loss:{:.4f}".format(loss.item()))
plt.xlabel("X")
plt.ylabel("Y")
plt.scatter(x,y)
plt.show()
截取几张图合并展示如下:
4. 模型评估与预测
4.1 模型评估
# 将模型设置为评估模式,这样在计算梯度时,不会考虑到dropout和batch normalization等操作
model.eval()
# 不需要计算梯度, 因为我们不需要进行模型优化
with torch.no_grad():
predictions = model(inputs)
loss = criterion(predictions, targets)
print("Final Loss:{:.4f}".format(loss.item()))
4.2 数据标准与预测
# 预测一个 100 平方米的房子的价格
area = torch.tensor([100.0])
# 对输入进行标准化
area_sta = dn_areas.encode(area)
price = model(area_sta)
# 对预测值还原,获取真实值
real_price = dn_prices.decode(price)
print(f'Predicted area {area.item()} got price {real_price.item():.4f}')
结果展示如下:
Final Loss:0.0083
Predicted area 100.0 got price 504.4887
训练完毕模型最终预测了一个100平方米的房子价格,并将标准值转化为真实值,成功获取了我们需要的值。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号