如何简单的预测集群容量? | 线性回归
集群容量预测是比较常见事情,由于预算限制,以及机柜限制。当集群因容量问题需要扩容时,需要提前N久规划。
- 当机柜充足,则提醒扩容
- 当机柜已满,则减少接入,查询大用户做好对象生命周期,保证集群容量缓慢增长
我是否需要逻辑回归?
看着集群容量视图,我果断问了问算法童靴,得到一个名词:逻辑回归。然后网上一查,随意一个逻辑回归图如下:
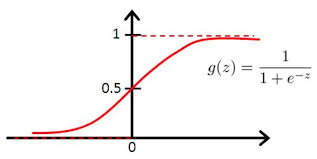
只看一眼,我就觉得这的确很像,这开头缓慢、中间爆发、后期稳定,三个阶段都很圆滑的展现出来了。然而我们以前都是直接预估一个平均增量,然后直接倍率乘以天数,咋感觉像是线性回归,这是咋回事?
逻辑回归 VS 线性回归
收集了下资料,原来他们场景并不一样,区别如下:
| 逻辑回归 | 解决回归问题 | 连续变量 | 符合线性关系 | 直观表达变量关系 |
|---|---|---|---|---|
| 线性回归 | 解决分类问题 | 离散变量 | 可以不符合线性关系 | 无法直观表达变量关系 |
对于我们这个场景,那么童靴说的也对,只不过看待角度不同,我总结了场景:
- 线性回归更适合容量预测,用来准备资源
- 逻辑回归则适合用来,容量不能扩容,是否可以抗到某某天
线性回归预测容量
线性回归,很符合平时看到的东西,比较好理解,自己也能计算,不过误差这一块就容易被忽视,因此都是保守预计,再按以往经验乘以倍率,得到最终结果。而以往经验这种东西多是口口相传,是短期难以获得的东西。如何从数据中分析出经验,似乎这才是真正的目的。
基础概念
\(y_i = 真实观测值\)
\(\bar{y_i} = 真实观测的平均值\)
\(\hat{y_i} = 预测值\)
\(R^2 = 决定系数,反映因变量的全部变异能通过回归关系被自变量解释的比例\)
\(R^2(y,\hat{y}) = 1 - \cfrac{ \sum_{i=1}^n(y_i - \hat{y}_i)^2}{ \sum_{i=1}^n(y_i - \bar{y}_i)^2}\)
对于R2可以通俗地理解为使用均值作为误差基准,看预测误差是否大于或者小于均值基准误差。
- R2_score = 1,样本中预测值和真实值完全相等,没有任何误差,表示回归分析中自变量对因变量的解释越好。
- R2_score = 0。此时分子等于分母,样本的每项预测值都等于均值。
- R2_score不是r的平方,也可能为负数(分子>分母),模型等于盲猜,还不如直接计算目标变量的平均值
注意事项
1、R2 一般用在线性模型中(非线性模型也可以用)
2、R2不能完全反映模型预测能力的高低,某个实际观测的自变量取值范围很窄,但此时所建模型的R2 很大,但这并不代表模型在外推应用时的效果肯定会很好。
3、数据集的样本越大,R²越大,因此,不同数据集的模型结果比较会有一定的误差,此时可以使用Adjusted R-Square (校正决定系数),能对添加的非显著变量给出惩罚:
\(R^2_{Adj} = 1 - (1 - R^2)\cfrac{n-p-1}{n-1}\)
n是样本的个数,p是变量的个数
简单代码实现
获取数据并转化
由于数据存在其他地方,我是查询导出为json,Pandas 可以直接有字典生产 DataFrame,是比较容易入手的。细节可以参考 用 Series 字典或字典生成 DataFrame
# 此次导入模块
import matplotlib.pyplot as plt
import pandas
from scipy import stats
from sklearn.metrics import r2_score
import numpy as np
# to pandas
df = pandas.DataFrame.from_dict(resource)
数据切割
存在多个集群,针对单个集群分开训练,由于不同集群上线时间不同,因此存在需要清空nan
x = df['ts']
y = df[cluster_name]
# 移除缺失值
start = 0
while np.isnan(y[start]):
start += 1
x = x[start:]
y = y[start:]
length = len(x)
train = int(length * 0.8)
train_x = x[:train]
train_y = y[:train]
test_x = x[train:]
test_y = y[train:]
训练与回归(单变量)
slope, intercept, r, p, std_err = stats.linregress(train_x, train_y)
def line_func(x):
return slope * x + intercept
cluster_model = list(map(line_func, test_x))
r2 = r2_score(test_y, cluster_model)
plt.scatter(test_x, test_y)
line_plot, = plt.plot(test_x, cluster_model)
plt.title("%s r<%0.4f> p<%0.4f> r2<%0.4f>" % (cluster_name, r, p, r2))
plt.legend([line_plot], ["regress"])
plt.show()
总结
挖掘数据下隐藏的信息,可以让我们更深入的了解业务与自身,从而更好的服务业务方,更准确的运营自身业务,实现共赢。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号