[Deep Learning] 深度学习中消失的梯度

　　好久没有更新blog了，最近抽时间看了Nielsen的《Neural Networks and Deep Learning》感觉小有收获，分享给大家。

　　了解深度学习的同学可能知道，目前深度学习面临的一个问题就是在网络训练的过程中存在梯度消失问题（vanishing gradient problem），或者更广义地来讲就是不稳定梯度问题。那么到底什么是梯度消失呢？这个问题又是如何导致的呢？这就是本文要分享的内容。

1. 消失的梯度

　　首先，我们将一个网络在初始化之后在训练初期的结果可视化如下：

　　

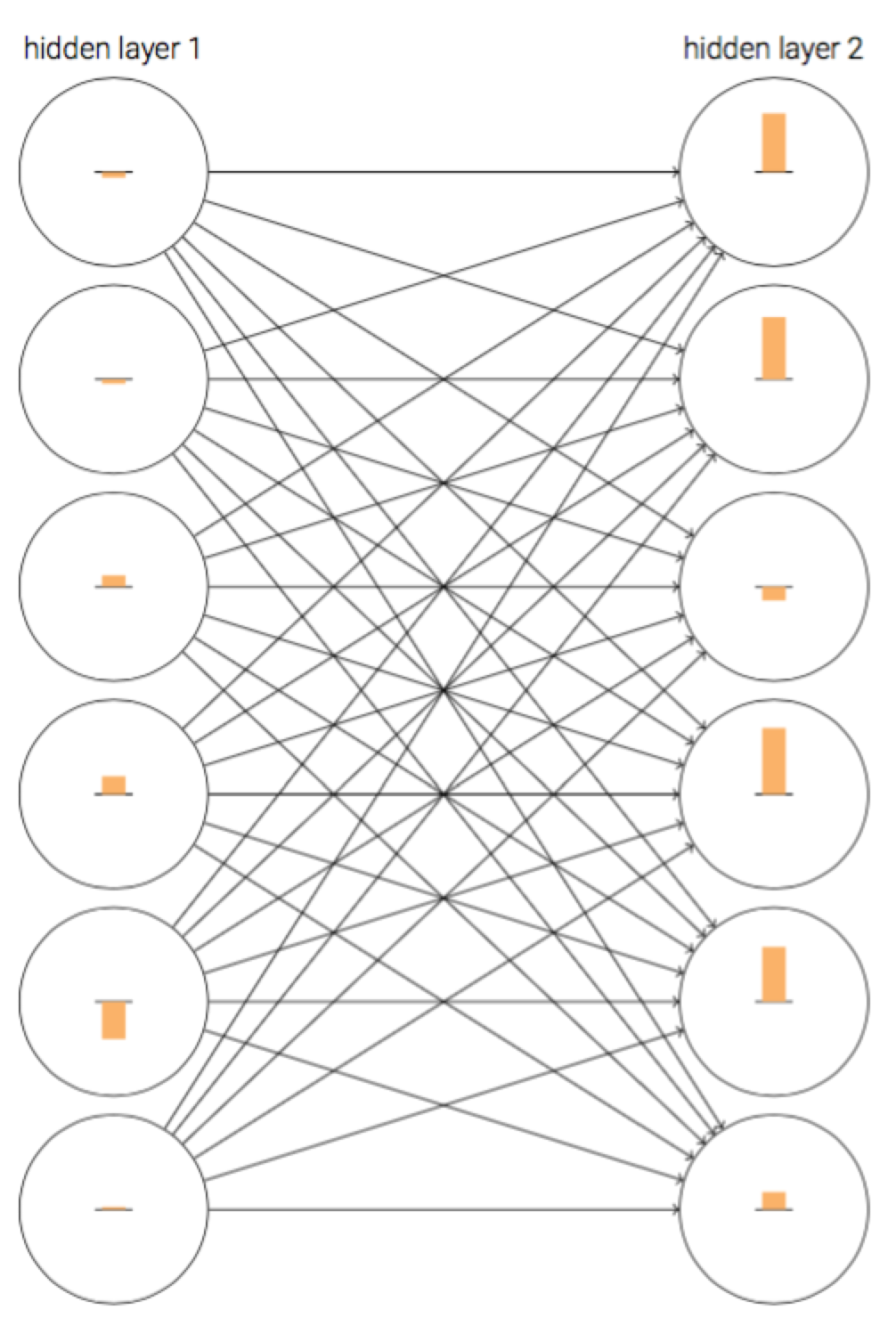
　　在上图中，神经元上的条可以理解为神经元的学习速率。这个网络是经过随机初始化的，但是从上图不难发现，第二层神经元上的条都要大于第一层对应神经元上的条，即第二层神经元的学习速率大于第一层神经元学习速率。那这可不可能是个巧合呢？其实不是的，在书中，Nielsen通过实验说明这种现象是普遍存在的。

　　我们再来看下对于一个具有四个隐层的神经网络，各隐藏层的学习速率曲线如下：

　　

　　可以看出，第一层的学习速度和最后一层要差两个数量级，也就是比第四层慢了100倍。 实际上，这个问题是可以避免的，尽管替代方法并不是那么有效，同样会产生问题——在前面的层中的梯度会变得非常大！这也叫做激增的梯度问题（exploding gradient problem），这也没有比消失的梯度问题更好处理。更加一般地说，在深度神经网络中的梯度是不稳定的，在前面的层中或会消失，或会激增，这种不稳定性才是深度神经网络中基于梯度学习的根本原因。

2. 什么导致了梯度消失？

　　为了弄清楚为何会出现消失的梯度，来看看一个极简单的深度神经网络：每一层都只有一个单一的神经元。下面就是有三层隐藏层的神经网络：

　　

　　我们把梯度的整个表达式写出来：

$\dfrac{\partial{C}}{\partial{b_{1}}}=\sigma^{\prime}(z_{1})\omega_{2}\sigma^{\prime}(z_{2})\omega_{3}\sigma^{\prime}(z_{3})\omega_{4}\sigma^{\prime}(z_{4})\dfrac{\partial{C}}{\partial{a_{4}}}$

　　为了理解每个项的行为，先看下sigmoid函数导数的曲线：

　　

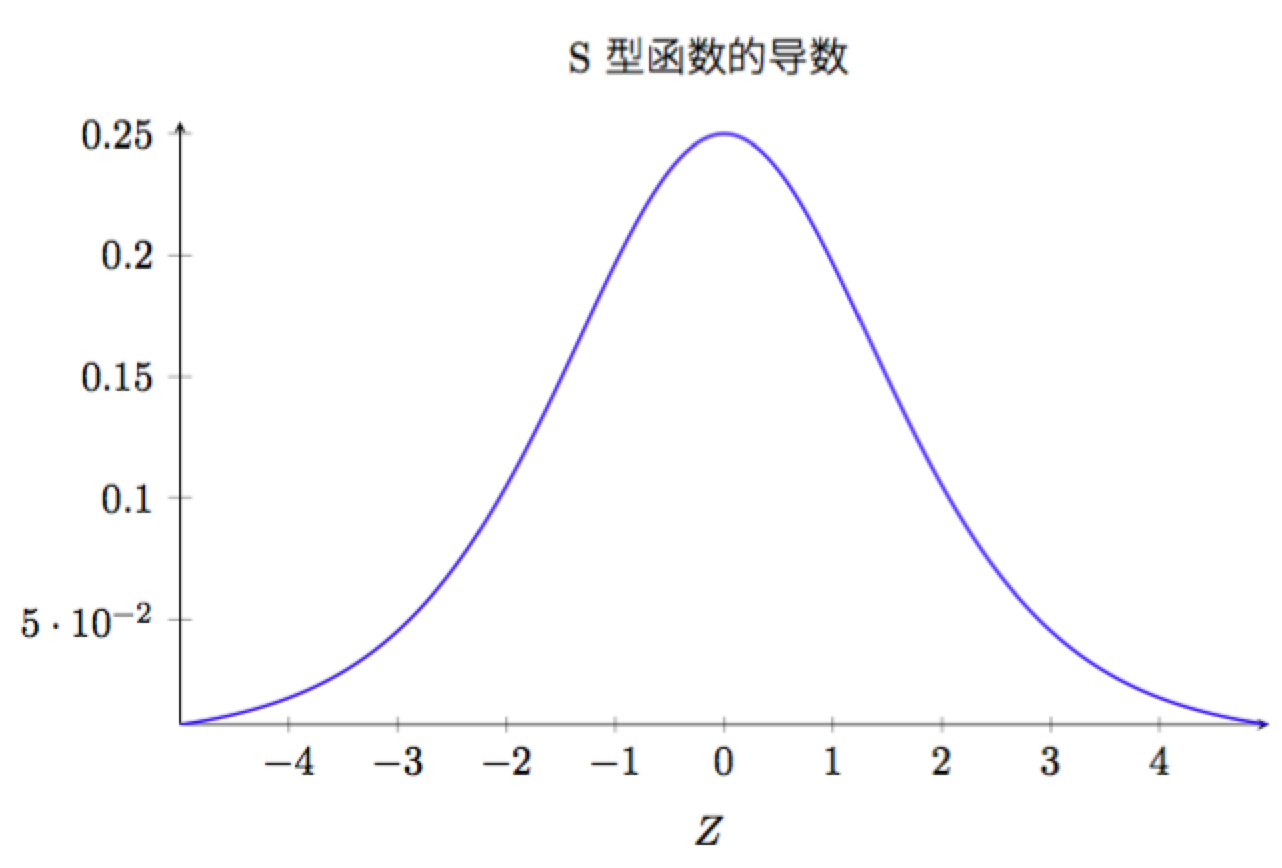
　　该导数在$\sigma^{\prime}(0)=\dfrac{1}{4}$时达到最高。现在，如果我们使用标准方法来初始化网络中的权重，那么会使用一个均值为0标准差为1的高斯分布。因此所有的权重通常会满足$|\omega_{j}|<1$。有了这些信息，我们发现会有$\omega_{j}\sigma^{\prime(z_{j})}<\dfrac{1}{4}$，并且在进行所有这些项的乘积时，最终结果肯定会指数级下降：项越多，乘积的下降也就越快。

　　下面我们从公式上比较一下第三层和第一层神经元的学习速率：

　　

 

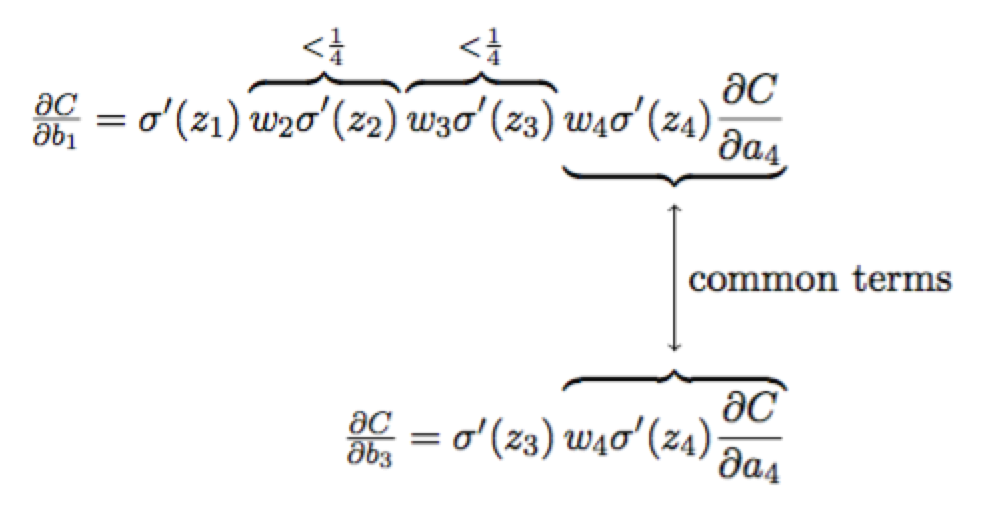
比较一下$\dfrac{\partial{C}}{\partial{b_{1}}}$和$\dfrac{\partial{C}}{\partial{b_{3}}}$可知，$\dfrac{\partial{C}}{\partial{b_{1}}}$要远远小于$\dfrac{\partial{C}}{\partial{b_{3}}}$。 因此，梯度消失的本质原因是：$\omega_{j}\sigma^{\prime}(z_{j})<\dfrac{1}{4}$的约束。

3. 梯度激增问题

举个例子说明下：

首先，我们将网络的权重设置得很大，比如$\omega_1=\omega_2=\omega_3=\omega_4=100$。然后，我们选择偏置使得$\sigma^{'}(z_{j})$项不会太小。这是很容易实现的：方法就是选择偏置来保证每个神经元的带权输入是$z_j=0$（这样$\sigma^{'}(z_{j})=\dfrac{1}{4}$）。比如说，我们希望$z_1=\omega_1*a_0+b_1$，我们只需要把$b_1=-100*a_0$即可。我们使用相同的方法来获取其他的偏置。这样我们可以发现所有的项$w_j*\sigma^{'}(z_j)$都等于100*1/4=25。最终，我们获得了激增的梯度。

4. 不稳定的梯度问题

　　不稳定的梯度问题：根本的问题其实并非是消失的梯度问题或者激增的梯度问题，而是在前面的层上的梯度是来自后面的层上项的乘积。当存在过多的层次时，就出现了内在本质上的不稳定场景。唯一让所有层都接近相同的学习速度的方式是所有这些项的乘积都能得到一种平衡。如果没有某种机制或者更加本质的保证来达成平衡，那网络就很容易不稳定了。简而言之，真实的问题就是神经网络受限于不稳定梯度的问题。所以，如果我们使用标准的基于梯度的学习算法，在网络中的不同层会出现按照不同学习速度学习的情况。

5. 参考文献

　　1. Michael Nielsen,《Neural Networks and Deep Learning》