平衡二叉搜索树
感谢清华大学邓俊辉老师的数据结构与算法慕课课程,真心好,带我入门。
一、AVL树
AVL树作为一种基本的平衡二叉搜索树(BBST:Binary Search Tree),是为了解决二叉搜索树(BST:Binary Search Tree)中"瘦高“型的树的问题。在BST中,对一个节点的访问,时间成本与其深度成正比,而一些"瘦高“型的树或者极端一点,直接退化list的树,其访问的时间复杂度退化成了O(N),而不是我们所期望的O(logN),BBST主要是在一定程度上控制树的高度,将一颗树控制成"矮胖"类型,其访问成本更低。
- 定义
AVL树为每个节点增加了一个平衡因子,其值是该节点的两棵子树的高度差,其值不会超过1(-1,0,1),对树高进行限制。
- insert
insert操作插入的节点,如果不影响全树的平衡因子失衡,则直接结束。如果引起平衡因子失衡,则插入的元素必定存在某一个节点的更加深的那棵子树上,从插入元素的祖先节点中找到离它最近的失衡的节点,然后在失衡路径上找到该最低失衡点的子节点和孙节点,以这三个节点,做一次“3+4”重构,就能将该节点由失衡转成平衡,而且其上所有的祖辈节点的失衡问题都能解决,因为总的来说,该节点的树高在变化后,并没有发生变化。对于一次insert操作,最好情况可能什么都不用做,只需要一次search操作,直接插入,最坏也只用一次“3+4”重构变换,O(1)的时间能解决。
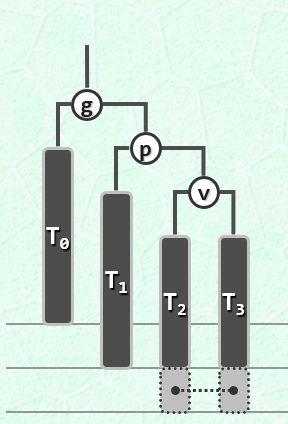
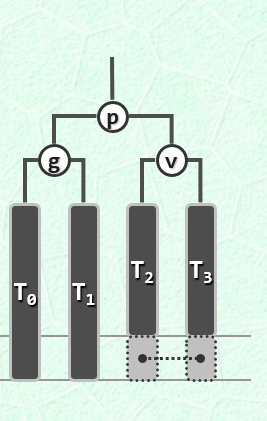
- remove
remove操作相对就会复杂一点,首先删除一个节点,如果导致平衡因子失衡,必然是因为删除的节点位于某一棵子树中较深节点的单节点,此时需要找到引起失衡在最低节点,然后以其子节点、孙节点这三个节点,做一次“3+4”重构。
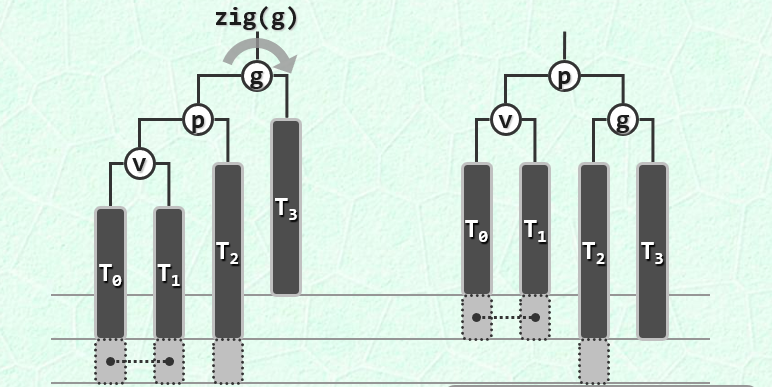
如图中,如果T2树原本已经有处于低处的节点,则此时节点P的深度未发生变化,remove操作结束,但是如果不存在,则remove使得节点P的高度降低了1,此时失衡情况可能会向上传导,继续导致失衡,如此反复,最坏情况会传导到树根处,所以remove操作的时间复杂度最坏情况是O(logN)。
二、Splay树
Splay树主要是针对在BST中,我们对某一节点进行访问后,很快又会访问改节点,或者访问该节点附近的节点。比如段页式存储中,我们对某一页面的内容访问,往往具有局部性。对于普通BST,一次静态访问,树的整体拓扑结构不发生变化,再次对该节点的访问都是需要相同的时间,而Splay树在每次访问某一节点时,都会将其提升到根部。提升的方式有两种,一种是自低向上,一种是自顶向下。自低向上虽然能将刚访问的节点提升至树的根部,但是对数的整体高度没有影响,而自顶向下会使访问路径上绝大部分节点高度减半,有着画龙点睛的精妙,我们来看看。
对于左右和右左这类之类型的节点,其变化自低向上和自顶向下的旋转变换没有区别。
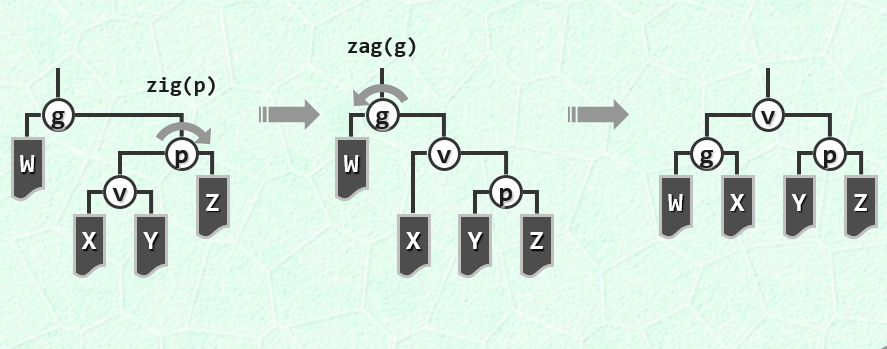
但是左左和右右这种类型的节点,就有区别了。
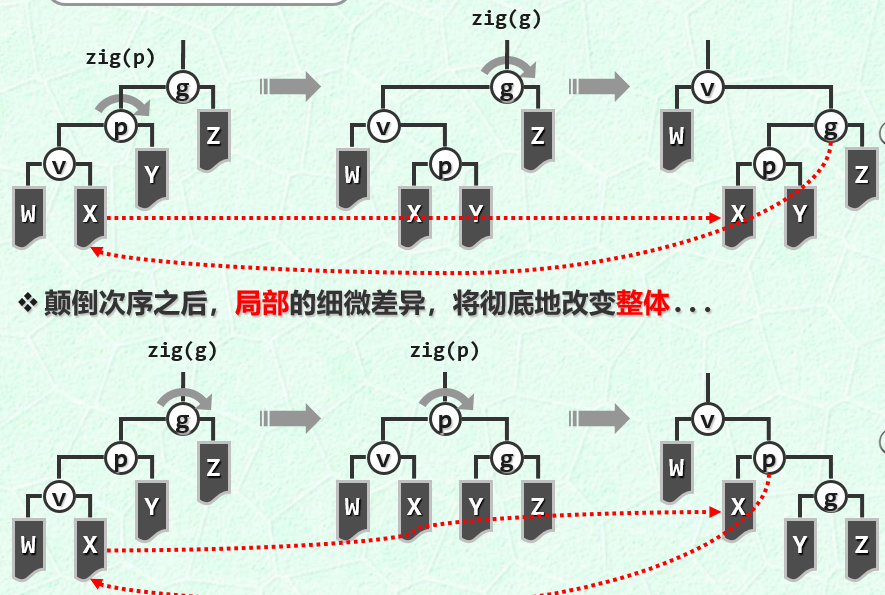
我的理解是这样的,注意对比自顶向下和自低向上的区别,其中X节点的位置,首先,变化后,我们假设子树W、X、Y、Z概率上具有相同的高度E(h),然后经过一次变换后,其树的高度在期望上来说,集中在节点V的右节点X上,一次变化使得节点V的高度提升了2,等于E(h)+2,我们将高度转移到了X上,在下次变换中节点V的右节点的树高更高,所有我们假设X具有更高的概率更大,但是在自低向上的变化中,X子树任然位于最底层,整体树高没有变化,而在自顶向下的变化中,X子树位的树高提升了一层,那么整体的树高就减少了。
就是这种关键的变化,使得Splay树具有调整树高的自适应性,优化整体的拓扑结构。
- insert
先调用Splay树的search操作,寻找和提升操作都完成了,直接在根节点处进行insert操作。
- remove
remove操作也一样,先进行search操作,然后在节点处直接进行remove操作。
三、B-Tree
B树也是对BST树的一种改进,比如我们知道内存的访问速度和磁盘的访问速度相差很大,速度差异达到了105级别,这种级别是1s之于1day级别的差别。所以我们希望减少对磁盘的访问次数,而每次访问读取的数据量可以多一点。这就是B树的思想,对于每个节点,我们可以存储多个数据,按照从小到大的排列,假设有n个数据,那么就会产生n+1路分支。
- 定义
假设每一个节点的关键码个数为n,以m阶B树为例:
- 每一个节点的分支数不能超过m,即n+1≤m
- 每一个节点的分支数不能少于⌈m/2⌉,即n+1≥⌈m/2⌉
- 根部的分支数大于1即可
- 所有外部节点的深度统一相等
此时m阶B树也被称为(⌈m/2⌉,m)树,比如4阶B树,也叫做(2,4)树;
- insert
在B树的插入操作中,如果会破坏B树的定义,肯定是插入的关键码节点数已经为饱和,为m-1个,插入后,关键码个数超过了限制,此时要进行分裂操作。
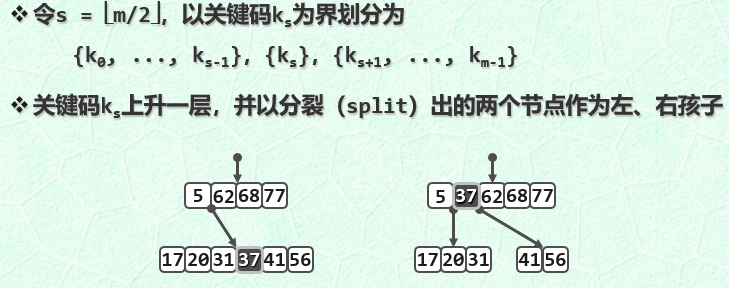
以该节点中的⌊m/2⌋位置为界分为两部分,分裂,然后将该节点提升至其父节点中,如图所示,但是可能会导致其父节点也产生上溢,最多不过到达根部,时间复杂度最坏情况下为O(logN).
- remove
remove操作如果破坏了B树的定义,必然是在该节点的分支数少于⌈m/2⌉,首先向该节点的左右邻居节点查询,是否有多的关键码可以“借”,先进行“左顾右盼”。
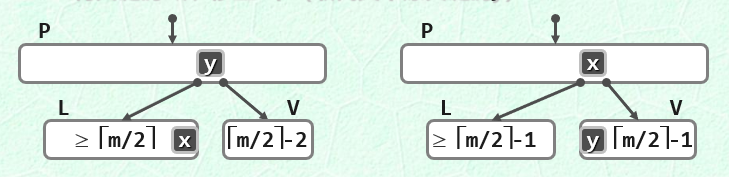
如果其左右邻居有多的节点可以借用,这进行一次移位操作,就可以完成删除操作,如果它的邻居没有多余的节点,其节点关键码刚好为⌈m/2⌉-1,则进行合并操作。
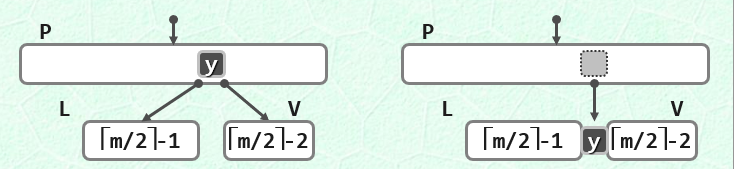
如图所示,但是这样会导致父节点其中关键码个数减少,相当于在父节点中删除一个关键码,此时再重复上述操作...如此反复,至多不过到根节点处结束,时间复杂度为O(logN).
四、B+Tree
B+树是对B树的一种改进,就像C和C++一样,假设每一个节点是以key-data的形式来保存数据,在B+树中,每一个节点只保存key值,而不保存该key值指向的data,这样,每一个节点可以保存的key值就更加多,叶节点中保留了所有的key值和对应的data,叶节点保留了所有的key值和data值,并且在所有叶节点增加了顺序访问的指针,每一个叶节点都指向其相邻的叶节点,这样,就组成了了一棵B+树,在进行insert操作时,肯定需要插入到叶节点处,如果发生上溢,节点的分裂过程与B树有点不同,在分裂的子节点中要保留key-data值,上溢时复制一份key值,上溢到父节点。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号