五子棋估值算法
| 目录 |
| 程序布局 |
| 估值算法 |
| 完整代码 |
程序布局
首先说明整个五子棋程序的整体布局。(用Java实现)
class Chess{ //界面类 Player player1 ; Player player2; ChessBox box; //其余界面显示相关函数; } class Player{
int code; //代号 1:选手1 2:选手2
ChessBox box;
abstract Point play(); //落子操作
int getLine(Point p, int i, int j) ;
}
class Person extends Player{
Point play(int x,int y );
}
class Robot extends Player{ //机器 int evaluate(Point, int, int); int Evaluate(Point); Point play(); } class ChessBox{ int chess_flag[15][15] //0:空 1:选手1 2:选手2 }
估值算法
要求分析
估值算法。要求给定棋盘上一个点,求出该点在当前棋局下的权值。若在该点落子后更容易接近胜利,则该点权值就高,越接近5子相连,权值越高。
则函数的形式为 int Evaluate(Point p);
首先考虑每个点有8个方向可以连子,每个方向上又有多种连子棋型,如活四、活三、死三等,而这些子又可能属于己方或者对方。活四与活三的权值自然不同。而同样是活三,己方的活三与对方的活三权值也不同,这样才能实现攻守的策略。假如现在棋局上同时有己方的活三和对方的活三,此时轮到我方落子,则正常情况下应当在己方活三上落子,使之成为活四,从而获胜。则计算机在判断棋局时,遇到己方活三,权值应当较高,遇到对方活三,权值应当较低。
以上即是对于估值函数所应达到的要求的分析。
方向问题
由于着眼处在于对棋型的判断,而不是方向,所以首先应该想个方法把方向问题先解决掉,这样在棋型判断时就能够对各个方向进行比较统一的处理,不至于棋型判断时对每个方向都写一段代码。
继续分析,在判断棋型时,着眼点在于棋子的相对位置,而常见棋型都呈线形排列,所以这个相对位置也就是顺序。相对位置、顺序,很容易想到要用一维的坐标解决。若取某一斜列(行、列),假设当前点的坐标为0,取右下(下、右、右上)为正方向,则在该斜列(行、列)上各点都能得到相应的坐标。如下图。
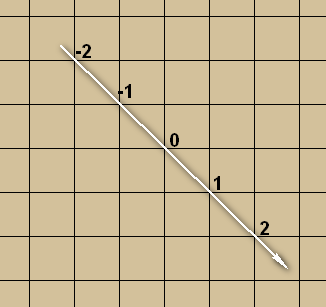
但若是同样的一维坐标,不同的方向,又会对应棋盘上不同的位置,也就是说,一维坐标转换到棋盘上的二维坐标,还需要一个方向。(额,想到这里,突然发现自己的思路明明就是极坐标啊。。。 ̄□ ̄||.........)
由此,我们需要达到这么一种要求:给定一个点、一个方向、一个相对坐标值,就能得到一个二维坐标,对应棋盘上一个点,进而可以获得任意一点的落子情况。所以我写了这么一个函数:
int getLine(Point p,int i,int j);
其中p为当前点,i为方向,取值为从1到8的整数,对应8个方向,j为相对于p点的坐标值。在函数体内要依据方向对p的x、y的值进行处理。返回该点的落子情况,0表示无子,1或2分别表示两个player,-1表示超出棋盘界。
代码如下:
1 int getLine(Point p, int i, int j) { // p:当前点 i:方向 j:坐标相对值 2 int x = p.x, y = p.y; 3 switch (i) { //对8个方向的处理 4 case 1 : 5 x = x + j; 6 break; 7 case 2 : 8 x = x + j; 9 y = y + j; 10 break; 11 ... 12 ... 13 case 8 : 14 x = x + j; 15 y = y - j; 16 } 17 if (x < 0 || y < 0 || x > 14 || y > 14) { // 越界处理 返回-1 18 return -1; 19 } 20 return box.getFlag(x,y); 21 } 22 }
棋型判断
对于方向的处理完成后,就是棋型的判断。判断棋型时需要区分当前所判断的棋型是哪一方的,假设当前所判断的棋型所属方的代号为plyer,则它的值可以是1或2,而要确定这个plyer是自己还是对方,就需要和自己的代号比对一下,假设自己的代号是me。则这个判断棋型的函数应该满足以下要求:给出一个点p,自己的代号me,一个plyer,能得出当前点对应plyer的权值。于是函数形式如下:
int evaluate(Point p, int me,int plyer);
然后结合已有的算法结构,参考下图(网上找到的)
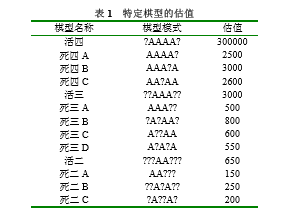
将棋型分为以下几种:
/* *: 当前空位置; 0: 其他空位置; 1: plyer(当前所计算的player的代号); 2: 3-plyer(对方的代号); */ 1.活四 :01111* 2.死四A :21111* 3.死四B :111*1 4.死四C :11*11 5.活三(近三位置) :111*0 6.活三(远三位置) :1110* 7.死三 :11*1
此外由于两个或多个方向上都有活二的棋型较为常见且胜率较高(见下图)。所以又增加对此种棋型的判断。
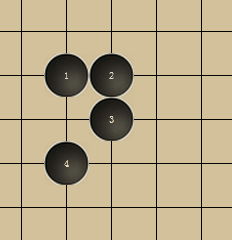
即在每一个方向的棋型判断中扫描011*0或111*0并计数,若最终计数值大于等于2,则权值增加一个较大的数值,否则不增加。
至此只要循环8次,每次循环中扫描各个棋型,并更新权值(设为value)即可。
代码如下:
1 int evaluate(Point p, int me,int plyer) { /* me:我的代号; plyer:当前计算的player的代号;*/ 2 int value = 0; 3 int numoftwo=0; 4 for (int i = 1; i <= 8; i++) { // 8个方向 5 // 活四 01111* *代表当前空位置 0代表其他空位置 6 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 7 && getLine(p, i, -3) == plyer && getLine(p, i, -4) == plyer 8 && getLine(p, i, -5) == 0) { 9 value += 300000; 10 if(me!=plyer){value-=500;} 11 System.out.print("+ 300000"); 12 continue; 13 } 14 ... 15 //计算011*0或111*0的个数 16 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 17 && getLine(p, i, -3) != 3-plyer&&getLine(p,i,1)!=3-plyer) { 18 numoftwo++; 19 } 20 ... 21 } 22 if(numoftwo>=2){ 23 value+=3000; 24 if(me!=plyer){ 25 value-=100; 26 } 27 } 28 return value; 29 }
其中每种棋型对value值所做的贡献要依据实际情况不断调整优化,优化不当就可能造成计算机放着活三不堵跑去堵活二了。。。
最终的估值函数 int Evaluate(Point p) 只要调用 int evaluate(Point p, int me,int plyer) 函数就可以获得p点的权值。
代码如下:
1 int Evaluate(Point p){ 2 return evaluate(p,code,1)+ evaluate(p,code,2); //code是调用者的代号 3 }
成果
最终程序核心算法只运用该估值算法,没有进行深度搜索。界面如下:
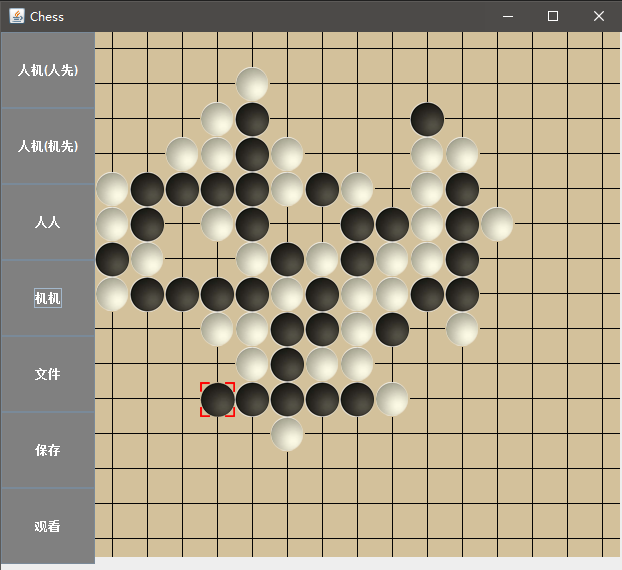
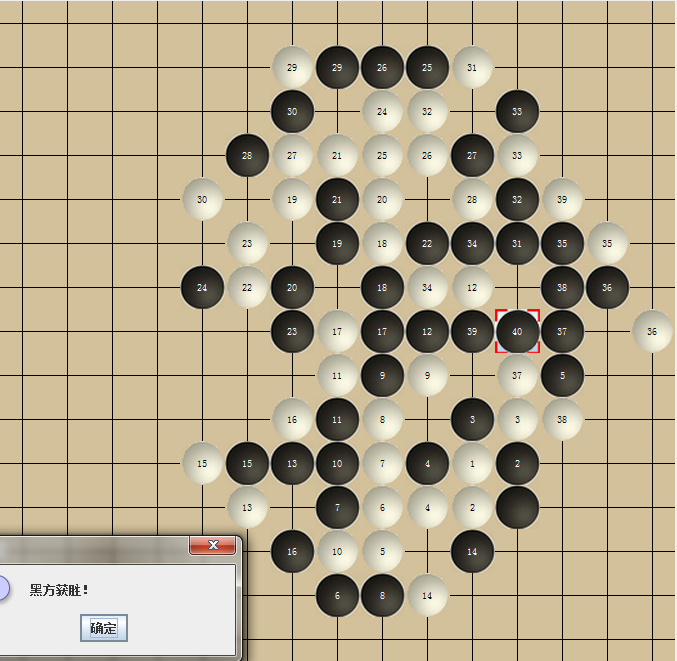
可见估值算法即便非常完美(当然这个算法离完美还差得远 ̄□ ̄||),依然无法做到立于不败之地,因为往往会出现对方有多个接近连五,以至于堵都堵不住。所以博弈还是必须要深度搜索的。
完整代码
最后贴出自己写的估值算法完整的代码(仅供参考,正确性未经严格验证):
1 int Evaluate(Point p){ 2 return evaluate(p, code,1) 3 + evaluate(p, code,2); 4 } 5 6 int evaluate(Point p, int me,int plyer) { // me:我的代号 plyer:当前计算的player的代号 7 int value = 0; 8 int numoftwo=0; 9 for (int i = 1; i <= 8; i++) { // 8个方向 10 // 活四 01111* *代表当前空位置 0代表其他空位置 下同 11 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 12 && getLine(p, i, -3) == plyer && getLine(p, i, -4) == plyer 13 && getLine(p, i, -5) == 0) { 14 value += 300000; 15 if(me!=plyer){value-=500;} 16 continue; 17 } 18 // 死四A 21111* 19 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 20 && getLine(p, i, -3) == plyer && getLine(p, i, -4) == plyer 21 && (getLine(p, i, -5) == 3 - plyer||getLine(p, i, -5) == -1)) { 22 value += 250000; 23 if(me!=plyer){value-=500;} 24 continue; 25 } 26 // 死四B 111*1 27 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 28 && getLine(p, i, -3) == plyer && getLine(p, i, 1) == plyer) { 29 value += 240000; 30 if(me!=plyer){value-=500;} 31 continue; 32 } 33 // 死四C 11*11 34 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 35 && getLine(p, i, 1) == plyer && getLine(p, i, 2) == plyer) { 36 value += 230000; 37 if(me!=plyer){value-=500;} 38 continue; 39 } 40 // 活三 近3位置 111*0 41 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 42 && getLine(p, i, -3) == plyer) { 43 if (getLine(p, i, 1) == 0) { 44 value += 750; 45 if (getLine(p, i, -4) == 0) { 46 value += 3150; 47 if(me!=plyer){value-=300;} 48 } 49 } 50 if ((getLine(p, i, 1) == 3 - plyer||getLine(p, i, 1) == -1) && getLine(p, i, -4) == 0) { 51 value += 500; 52 } 53 continue; 54 } 55 // 活三 远3位置 1110* 56 if (getLine(p, i, -1) == 0 && getLine(p, i, -2) == plyer 57 && getLine(p, i, -3) == plyer && getLine(p, i, -4) == plyer) { 58 value += 350; 59 continue; 60 } 61 // 死三 11*1 62 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 63 && getLine(p, i, 1) == plyer) { 64 value += 600; 65 if (getLine(p, i, -3) == 0 && getLine(p, i, 2) == 0) { 66 value += 3150; 67 continue; 68 } 69 if ((getLine(p, i, -3) == 3 - plyer||getLine(p, i, -3) == -1) && (getLine(p, i, 2) == 3 - plyer||getLine(p, i, 2) == -1)) { 70 continue; 71 } else { 72 value += 700; 73 continue; 74 } 75 } 76 //活二的个数 77 if (getLine(p, i, -1) == plyer && getLine(p, i, -2) == plyer 78 && getLine(p, i, -3) != 3-plyer&&getLine(p,i,1)!=3-plyer) { 79 numoftwo++; 80 } 81 //其余散棋 82 int numOfplyer = 0; // 因为方向会算两次? 83 for (int k = -4; k <= 0; k++) { // ++++* +++*+ ++*++ +*+++ *++++ 84 int temp = 0; 85 for (int l = 0; l <= 4; l++) { 86 if (getLine(p, i, k + l) == plyer) { 87 temp++; 88 } else 89 if (getLine(p, i, k + l) == 3 - plyer 90 || getLine(p, i, k + l) == -1) { 91 temp = 0; 92 break; 93 } 94 } 95 numOfplyer += temp; 96 } 97 value += numOfplyer * 15; 98 if (numOfplyer != 0) { 99 } 100 } 101 if(numoftwo>=2){ 102 value+=3000; 103 if(me!=plyer){ 104 value-=100; 105 } 106 } 107 return value; 108 } 109 110 int getLine(Point p, int i, int j) { // i:方向 j:相对p的顺序值(以p为0) p:当前点 111 int x = p.x, y = p.y; 112 switch (i) { 113 case 1 : 114 x = x + j; 115 break; 116 case 2 : 117 x = x + j; 118 y = y + j; 119 break; 120 case 3 : 121 y = y + j; 122 break; 123 case 4 : 124 x = x - j; 125 y = y + j; 126 break; 127 case 5 : 128 x = x - j; 129 break; 130 case 6 : 131 x = x - j; 132 y = y - j; 133 break; 134 case 7 : 135 y = y - j; 136 break; 137 case 8 : 138 x = x + j; 139 y = y - j; 140 } 141 if (x < 0 || y < 0 || x > 14 || y > 14) { // 越界处理 142 return -1; 143 } 144 return box.getFlag(x,y); 145 }
END
2015.9.21 10:53


 浙公网安备 33010602011771号
浙公网安备 33010602011771号