OO第一单元总结
第一单元总结
写在前面的话
经过从pre开始的漫长的一个月,带着惊喜和遗憾,OO的第一单元谢幕了。
但是在三次作业的设计,实现,debug以及总结交流的过程中,我认识到OO的学习和体会还远未结束,毫不夸张的说,现在学习OO的不适应,仿佛打开一扇门时因为直视其透出的亮光而头晕目眩的结果。所以接下来所要做的,是在克服上述的眩晕感之后站稳脚跟,为以后更进一步的学习打下坚实的基础。
我在上学期上过李波老师所开设的Java一般专业课,在这门课上,李波老师极少向我们展示Java代码,他把课堂上的绝大多数时间花在向我们讲述Java的设计思想以及他过去的经验上。许多同学(包括我)因为他极少向我们介绍Java语法而感到困惑。而在oo的pre和第一单元的学习过程中,我懵懵懂懂的领会了当时李波老师的意图。我体会到,当前我学习Java或者说学习面向对象编程的困难主要来源于两方面:
一方面是像学习所有编程语言一样的,来自于语言本身所带有的种种复杂性,尽管设计者在设计之初怀着尽可能简化复杂度的意图,但是在编程语言的复杂度和功能强大之间做trade-off的过程中,就无可避免的面临复杂度的提高。对于Java,数目繁多的官方库乃至第三方库是其复杂度的体系。体现在我的学习过程中就是:在代码的实现过程中,我常常为了避免可能出现的bug而阅读某个数据结构许多的说明。比如第一和第二次作业中重写hashtable的equals和hashcode方法,第三单元中由于使用了TreeMap这个数据结构使得多项式这个类必须实现comparable这个接口。
另一方面来源于对面向对象这一思想的掌握,我在大一经过C语言设计基础以及数据结构这两门课的磨(zhe)练(mo),面对过程编程的习惯已经是根深蒂固,即使接触了面对对象的核心观点,也难免在面对过程里来回转圈,白白耗费许多精力。
总而言之,千里之行始于足下,尽管oo思想博大精深,但是我相信通过自己努力的学习,还是能够有所收获,有所成长的,毕竟古人有云:“天道酬勤”。
基于度量对程序结构的分析
1.第一次作业
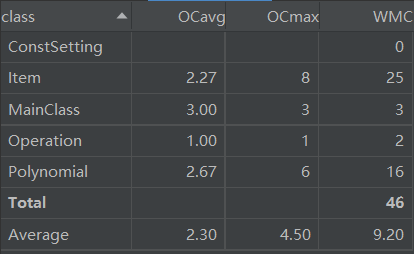
第一次作业中我建立了五个类,其中MainClass为主类,Polynomial和Item是用来对于多项式和项的两个类,Operation是一个静态类,常用的操作被抽象成方法放入这个类。ConstSetting被用来放置一些常数和字符串。
从图中可以看出,这几个类中Item的复杂度是最高的,分析具体代码可知,在Item的构造方法里实现了从Item的字符串中解析出该项的系数和指数的功能,因此复杂度较高。

这是本次作业的基本架构,可以看出,Item这个类是表达式类的原子单位,MainClass通过调用Operation中的静态方法来创建Polynomial和Item对象并将它们合并。这种代码的好处是易于理解实现,坏处是没有将常数因子和幂函数因子分开,使得第二次代码需要重构(第二次代码没过中测QAQ)。
整个表达式的读入过程如下:
字符串预处理(为后面重构埋下伏笔):去除字符串内的空格,合并相邻的多个加减号;
匹配正则表达式:
String REGEX = ([+-]?([+-]?\d*(x(\^[+-]?\d+)?)?\*)*([+-]?\d*(x(\^[+-]?\d+)?)?));
使用Pattern类和Matcher类来匹配上述正则表达式,通过Matcher类中的group方法返回一个又一个的符合格式的项的字符串,再将这个字符串输入Item这个类的构造方法中得到一个项的对象。
2.第二次作业
第二次作业本想采用递归下降语法分析的方法来进行,但由于对该方法的精髓理解不够深入,导致只写出了个半吊子( 💩山)出来,代码复杂度各种爆表,下面欢迎进入OO饭堂环节:
代码复杂度:
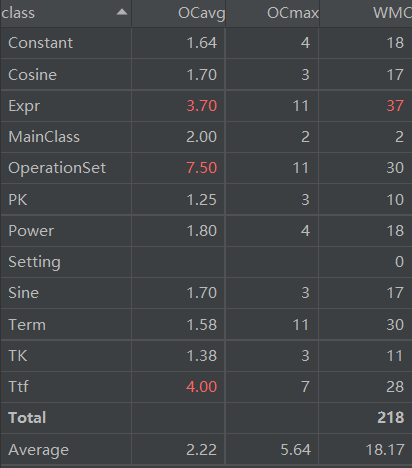
图中Constant,Power,Sine,Cosine为实现了Factor接口的四个因子类,Term为集成了四种因子的项,而表达式类则是一个封装了许多项的类,其中项的组织方式是通过HashTable来聚合而成的,而HashTable的键是一个项中的三角函数的指数。MainClass通过OperationSet中的静态方法来得到。
可以看出,复杂度飘红的类有Expr,Operation,Ttf。解释一下原因 😭: 底层项和因子的抽象方法没写好,导致在Expr中需要大量重复代码,同时Operation由于实现的是半吊子( 💩山)递归下降,导致复杂度爆表(也爆出了许多bug),对于Ttf,作为一个工厂模式中的工厂类,还被我塞入了一些不知道应该放哪里的方法,也导致其复杂度巨大。
UML图:
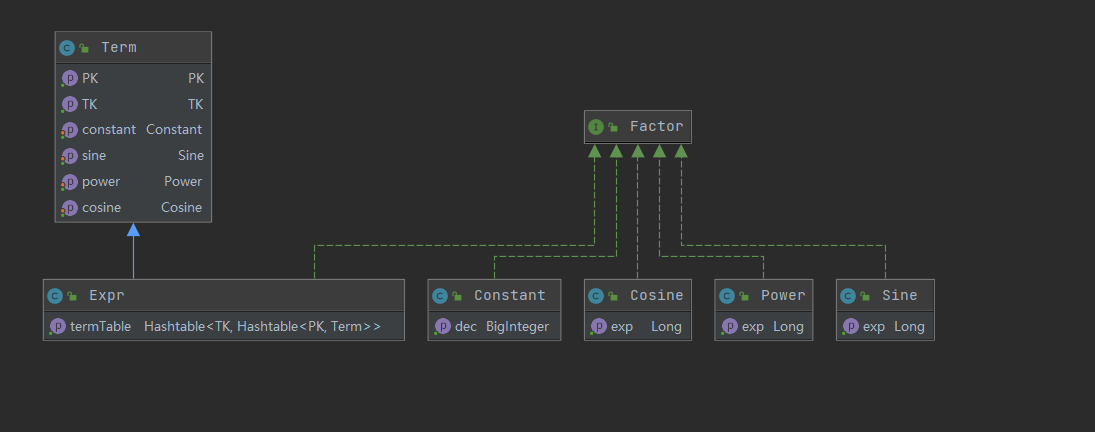
在我做完第三次作业回头看这个第二次作业的架构时,我觉得它依然有许多值得改进的地方,比如多项式是否应实现Factor接口?这里之所以实现了Factor接口是因为表达式中存在着多项式因子,使用工厂模式返回的因子还可能是一个表达式。
上述架构的另一个致命缺陷是难以扩展,这导致了第三次作业的重构。
第三次作业:
第三次作业真是一言难尽,我体会到了什么叫做在泥潭中苦苦挣扎,最开始我以为Java没有类似于C语言中的自引用指针,后来发现一个类里面可以定义自身的引用类型,这解决了第三次作业中表达式因子循环嵌套的造成的递归问题。后来我又因为使用了TreeMap来存表达式,导致需要给每一个表达式排一个线性序,在数学上这是可能的,但是代码实现起来过于复杂且会产生数量令人难以忍受的bug。(后来有人告诉我可以先实现其字符串输出功能,再将其字符串的字典序作为表达式的线性序,不过那已经是后话了)。最后实在没办法,我放弃了一开始选用的TreeMap,改用了之前使用的HashTable,这样就通过了中测,但由于测试不够充分,许多设计也不够完善,最后在强测中得分不是很理想。
类复杂度:
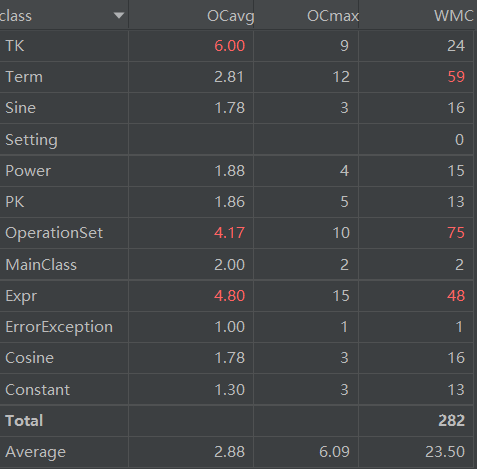
本次类的复杂度较上次作业上升了不少。一方面是作业本身复杂了一点,但是主要还是因为架构的不合理(第n次鞭尸架构)导致了事倍功半的效果。
第三次作业最大的败笔,就是前期在自己不熟悉的TreeMap上空耗大量的时间导致后来匆匆忙忙换用了HashTable没有时间充分解决程序中的bug。讲道理每个人都需要学习,知识都是从不熟到熟,但是为什么说在TreeMap上空耗了大量时间呢?原因是我使用TreeMap前没有好好看清TreeMap的注意事项,导致架构的设计直接出现问题。
另一个败笔,是没有进行最简单的合并处理,我没有合并一些基本的同类项,导致类似8个$(1+x)$连乘这样的样例会出现巨长的求导结果。
UML图:(从图中可以看到密密麻麻的耦合关系)
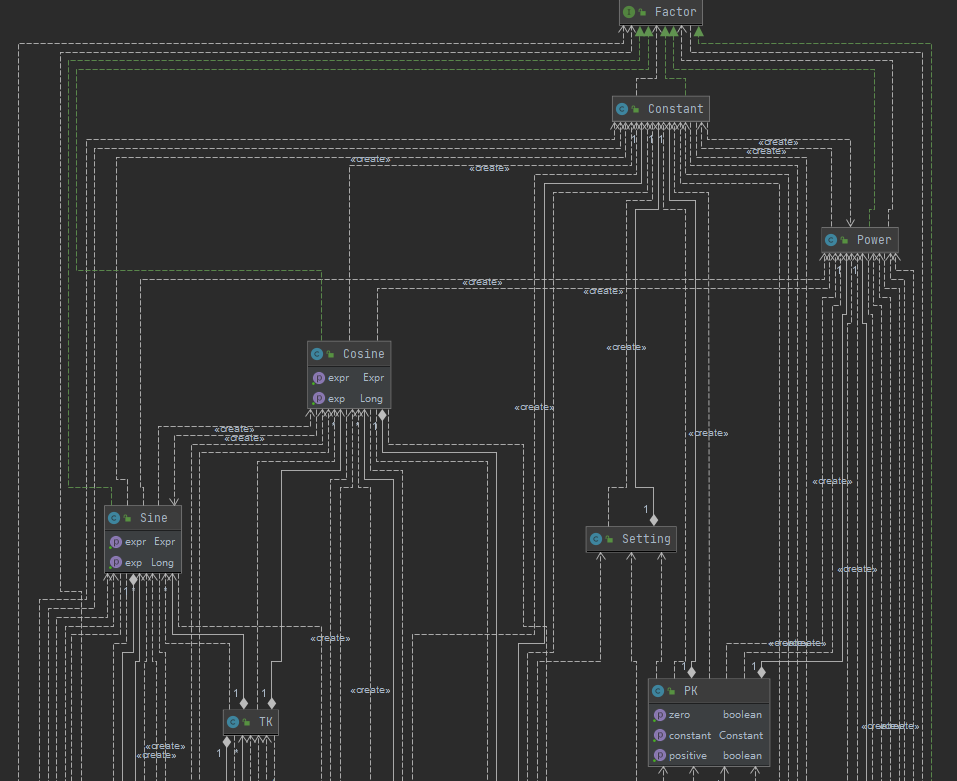
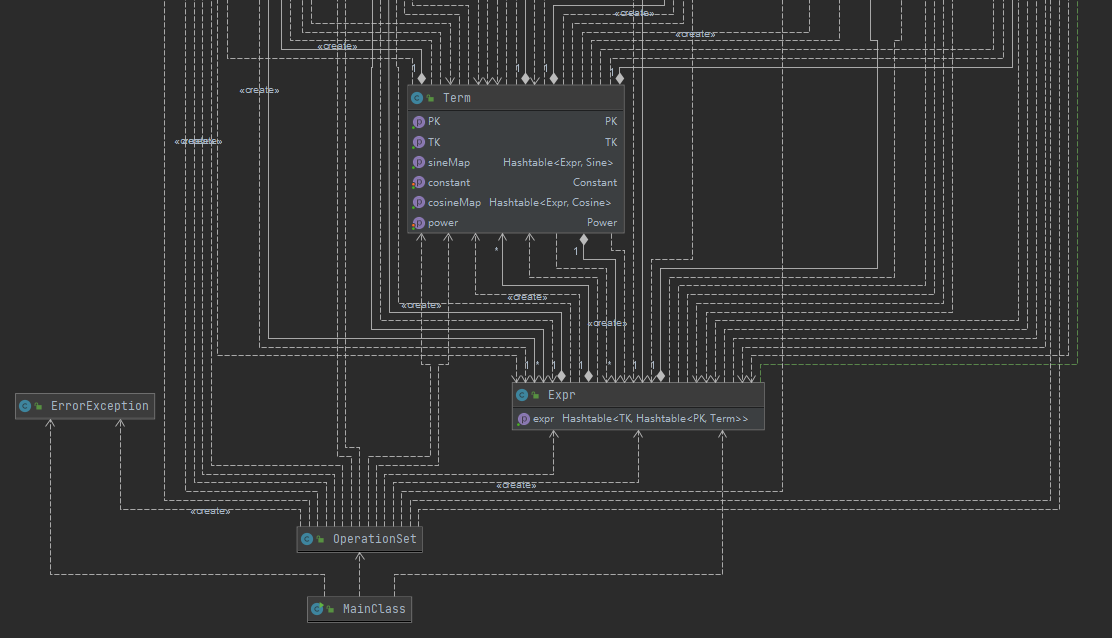
由于三角函数内可以嵌套表达式因子,表达式因子在HashTable中需要由三角函数构成的键来进行索引,本次作业的架构惨不忍睹,可谓真正 💩山(如果助教大人您看这篇文章时在吃饭的话请原谅我,我发誓这是我在这篇文章里最后一次用这个词语了,毕竟没有比上面这个架构更大的。。。。了)
最开始我的想法是万物皆函数,包括自变量x本身也是自己的正比例函数,通过这种视角出发来进行架构的设计可能会是愉快的事情,但是后来我发现这与递归下降语法分析的思想相抵触,毕竟递归下降是有一个层次结构的。而此种设计则是扁平的(当然也可以把数据结构和字符串处理分开考虑),所以为了设计出合乎递归下降的数据结构,我还是使用了分层的做法,但是由于我使用了HashTable,这一次的键就没有上一次的方便,一个项中的正余弦不能简单的用其幂指数来指代了,而需要将他们包括的多项式也考虑进去。这也就导致了上面这张巨复杂的UML图。
程序bug分析
第一次作业中的bug
第一次作业过的很好,中测过了之后强测中没有出现bug。
第二次作业中的bug
第二次作业中的bug有9个之多,究其原因是在优化幂函数指数为1或系数为1的情况时,要么少输出了乘号,要么少输出了或者多输出了加号或者括号。
第三次作业中的bug
这次的bug出在取字符串下一个字符时没有考虑遇到边界的情况以及用Long去存读入的指数导致爆Long。
发现别人bug所采用的做法
我一般是会从一些原子的样例测试起,如x,1x,-x,+x,-1x,+1*x,+-x,-+x,......通过逐渐复杂化来尽可能的遍历程序中所用的分支。这种做法比较费时间,适用性不高,不过在这次作业中是足够的。(就是我太懒了QAQ)
重构的心得体会
重构时一定注意数据的处理和数据的组织是两件事情,数据的处理多半取决于数据的输入形式,在本单元作业中常常难以体现数据之间的逻辑关系,而数据的组织则需要以最自然的方式也就是数据本身的逻辑关系来组织到一起。
我之前设想了一种组织方式,从数学的角度出发,根据本题出现的三种基本函数,构造三个类,这三个类除了体现自己的函数类型以外,还有一个表达式的属性域,表达式的唯一一个属性,则是一个项的ArrayList,而项这个类的属性域,则包括了四个属性:常数,幂函数,正弦函数的ArrayList,余弦函数的ArrayList,这种数据结构的一个关键是:当三种类(幂函数,正余弦函数)其中包含的表达式为x时,属性域里的表达式那一个引用便会被设置为空引用,来表示其中嵌套了自变量x。
举个例子,下面的函数:
(cos(x * * 2)) * * 2
会被视为一个多层嵌套的例子,首先会有一个幂函数的对象,其指数是2,其表达式域指向一个余弦函数的对象,在这个余弦函数的对象里,其表达式域指向了一个幂函数的对象,这个幂函数的对象的表达式域则为空指针。
这样,我们就可以很自然的实现一个导数的链式法则。而导数的莱布尼兹法则,则可以通过将一个项里面的所有因子加到一个ArrayList,求导其中一个因子并将结果与其他所有因子相乘,对所有因子重复上述操作,就实现了莱布尼兹法则。
心得体会
三次作业下来,尽管分数不理想,也花了许许多多的时间精力,但是依然十分满意,原因是逐渐认识到了编程的复杂性以及面向对象的价值与关键,面向过程时作为教程的一部分的题目往往不会过于复杂(我做过的最复杂的是处理北京的地铁线路,现在想想,如果用Java的话难度骤减,当然,这是事后诸葛亮),但是在实际解决工程问题时,处理复杂性的难度相比起性能优化恐怕也不遑多让,这时面向对象的思想便会大放光彩。
在本篇文章的最后,我想请州长夫人唱一首《hello, 夏威夷》(×对不起拿错剧本了)我想摘抄《Java编程思想》上关于面向对象的几个核心观点来做一个结尾:
- 万物皆对象;
- 程序是对象的集合,他们通过发送消息来告诉彼此所要做的;
- 每个对象都有自己的由其他对象所构成的存储;
- 每个对象都拥有其类型;
- 某一特定类型的所有对象都可以接受同样的消息;
本博客的Notion链接:https://www.notion.so/6d65fc4d3dbc47509a535cee60a3b498
本文作者:Max_Season
本文链接:https://www.cnblogs.com/maxorao/p/14589811.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步