【原】Coursera—Andrew Ng机器学习—编程作业 Programming Exercise 2——逻辑回归

作业说明

　　Exercise 2，Week 3，使用Octave实现逻辑回归模型。数据集  ex2data1.txt ，ex2data2.txt

　　实现 Sigmoid 、代价函数计算Computing Cost 和 梯度下降Gradient Descent。

 

文件清单

• ex2.m - Octave/MATLAB script that steps you through the exercise
  
• ex2 reg.m - Octave/MATLAB script for the later parts of the exercise
• ex2data1.txt - Training set for the first half of the exercise
• ex2data2.txt - Training set for the second half of the exercise
• submit.m - Submission script that sends your solutions to our servers
• mapFeature.m - Function to generate polynomial features
• plotDecisionBoundary.m - Function to plot classifier’s decision boundary
• [*] plotData.m - Function to plot 2D classification data
• [*] sigmoid.m - Sigmoid Function
• [*] costFunction.m - Logistic Regression Cost Function
• [*] predict.m - Logistic Regression Prediction Function
• [*] costFunctionReg.m - Regularized Logistic Regression Cost

　　* 为必须要完成的

结论

     正则化不涉及第一个 θ₀

逻辑回归

　　背景：大学管理员，想要根据两门课的历史成绩记录来每个是否被允许入学。

　　ex2data1.txt ，前两列是两门课的成绩，第三列是y值 0 和 1。

一、绘制数据图

　　 plotData.m：

  positive = find(y == 1);
  negative = find(y == 0);
  
  plot(X(positive,1),X(positive,2),'k+','MarkerFaceColor','g',
    'MarkerSize',7);
  hold on;
  plot(X(negative,1),X(negative,2),'ko','MarkerFaceColor','y',
    'MarkerSize',7);

  　　运行效果如下：

 

二、sigmoid 函数

function g = sigmoid(z)
% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
%               vector or scalar).
  g = 1 ./ (1 + exp(-z));
end

 三、代价函数

　　costFunction.m：

function [J, grad] = costFunction(theta, X, y)

　　m = length(y); % number of training examples

　　part1 = -1 * y' * log(sigmoid(X * theta));
　　part2 = (1 - y)' * log(1 - sigmoid(X * theta));
　　J = 1 / m * (part1 - part2); 
    
　　grad = 1 / m * X' *((sigmoid(X * theta) - y));

end

 四、预测函数

　　输入X和theta，返回预测结果向量。每个值是 0 或 1

function p = predict(theta, X)
%PREDICT Predict whether the label is 0 or 1 using learned logistic 
%regression parameters theta
%   p = PREDICT(theta, X) computes the predictions for X using a 
%   threshold at 0.5 (i.e., if sigmoid(theta'*x) >= 0.5, predict 1)

m = size(X, 1); % Number of training examples

% 最开始没有四舍五入，导致错误
p = round(sigmoid(X * theta));

end

五、进行逻辑回归　　

　　ex1.m 中的调用：

　　加载数据：

data = load('ex2data1.txt');
X = data(:, [1, 2]); y = data(:, 3);

[m, n] = size(X);

% Add intercept term to x and X_test
X = [ones(m, 1) X];

initial_theta = zeros(n + 1, 1);

  　 调用 fminunc 函数

options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, cost] = ...
    fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

 四、绘制边界线

　　plotDecisionBoundary.m

function plotDecisionBoundary(theta, X, y)
%PLOTDECISIONBOUNDARY Plots the data points X and y into a new figure with
%the decision boundary defined by theta
%   PLOTDECISIONBOUNDARY(theta, X,y) plots the data points with + for the 
%   positive examples and o for the negative examples. X is assumed to be 
%   a either 
%   1) Mx3 matrix, where the first column is an all-ones column for the 
%      intercept.
%   2) MxN, N>3 matrix, where the first column is all-ones

% Plot Data
plotData(X(:,2:3), y);
hold on

if size(X, 2) <= 3
    % Only need 2 points to define a line, so choose two endpoints
    plot_x = [min(X(:,2))-2,  max(X(:,2))+2];

    % Calculate the decision boundary line
    plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));

    % Plot, and adjust axes for better viewing
    plot(plot_x, plot_y)
    
    % Legend, specific for the exercise
    legend('Admitted', 'Not admitted', 'Decision Boundary')
    axis([30, 100, 30, 100])
else
    % Here is the grid range
    u = linspace(-1, 1.5, 50);
    v = linspace(-1, 1.5, 50);

    z = zeros(length(u), length(v));
    % Evaluate z = theta*x over the grid
    for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z'; % important to transpose z before calling contour

    % Plot z = 0
    % Notice you need to specify the range [0, 0]
    contour(u, v, z, [0, 0], 'LineWidth', 2)
end
hold off

end

 

 

---

 

正则化逻辑回归

　　背景：预测来自制造工厂的微芯片是否通过质量保证（QA）。 在QA期间，每个微芯片都经过两个测试以确保其正常运行。

　　ex2data2.txt ，前两列是测试结果的成绩，第三列是y值 0 和 1。

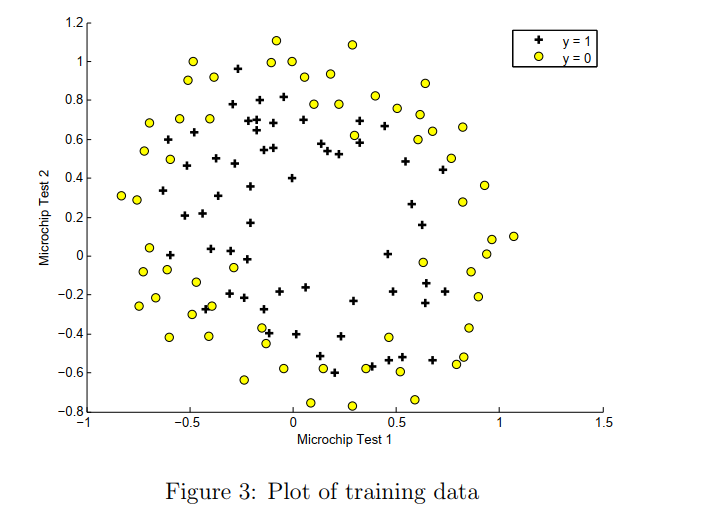
　　只有两个feature，使用直线不能划分。

　　为了让数据拟合的更好，使用mapFeature函数，将x1，x2两个feature扩展到六次方。

　　六次方曲线复杂，容易造成过拟合，所以需要正则化。

 

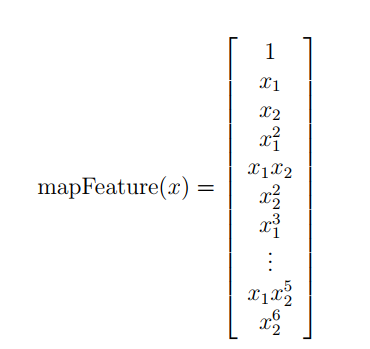
　　mapFeature.m

function out = mapFeature(X1, X2)
% MAPFEATURE Feature mapping function to polynomial features
%
%   MAPFEATURE(X1, X2) maps the two input features
%   to quadratic features used in the regularization exercise.
%
%   Returns a new feature array with more features, comprising of 
%   X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
%
%   Inputs X1, X2 must be the same size
%

degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

end 

二、代价函数

　　注意：θ₀不参与正则化。

　　正则化逻辑回归的代价函数如下，分为三项：

　 

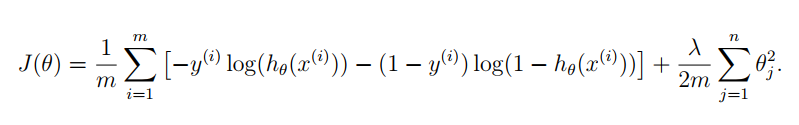
　　梯度下降算法如下：

 

 　　coatFunctionReg.m 如下：

function [J, grad] = costFunctionReg(theta, X, y, lambda)
  m = length(y); % number of training examples

  % theta0 不参与正则化。直接让变量等于theta，将第一个元素置为0，再参与和 λ 的运算
  t = theta;  t(1) = 0; 
  
  % 第一项
  part1 = -y' * log(sigmoid(X * theta));
  % 第二项
  part2 = (1 - y)' * log(1 - sigmoid(X * theta));
  
  % 正则项
  regTerm = lambda / 2 / m * t' * t;
  J = 1 / m * (part1 - part2) + regTerm; 

  % 梯度
  grad = 1 / m * X' *((sigmoid(X * theta) - y)) + lambda / m * t;

end

　　em2_reg.m 里的调用

% 加载数据
data = load('ex2data2.txt');
X = data(:, [1, 2]); y = data(:, 3);

% mapfeature
X = mapFeature(X(:,1), X(:,2));

% Initialize fitting parameters
initial_theta = zeros(size(X, 2), 1);
lambda = 1;

% 调用 fminunc方法
options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, J, exit_flag] = ...
    fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);

三、参数调整

 　　（1）使用正则化之前，决策边界曲线如下，可以看到存在过拟合现象：

 

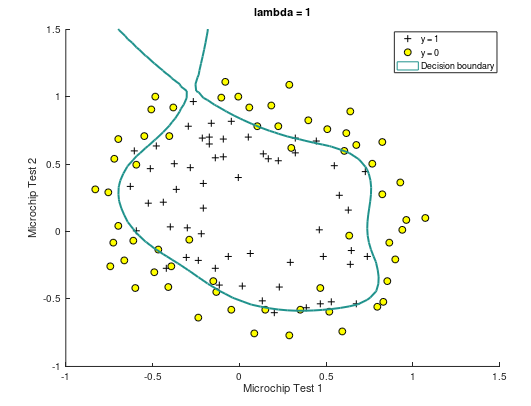
 　（2）当 λ = 1，决策边界曲线如下。此时训练集预测准确率为  83.05%

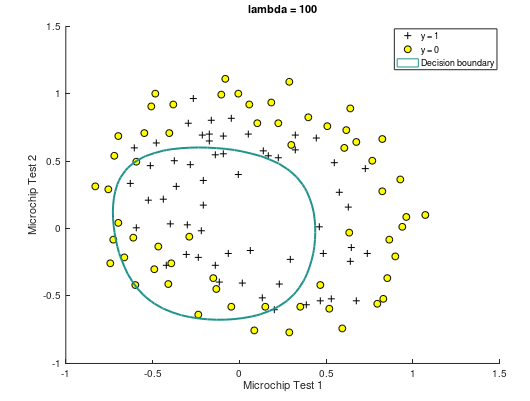
 　（3）当 λ = 100，曲线如下。此时训练集预测准确率为 61.01%

 

完整代码

https://github.com/madoubao/coursera_machine_learning/tree/master/homework/machine-learning-ex2/ex2