【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 13—Clustering 聚类

Lecture 13 聚类 Clustering

13.1 无监督学习简介  Unsupervised Learning Introduction

现在开始学习第一个无监督学习算法：聚类。我们的数据没有附带任何标签，拿到的数据就是这样的:

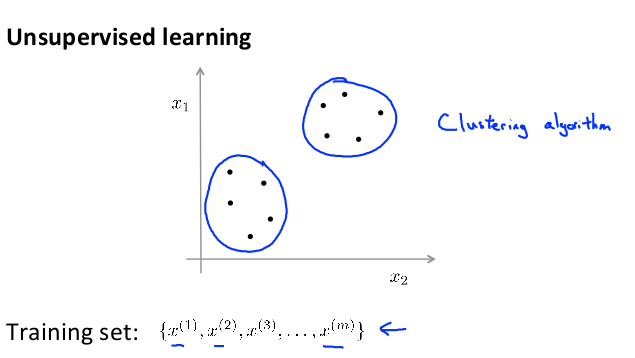
例子：

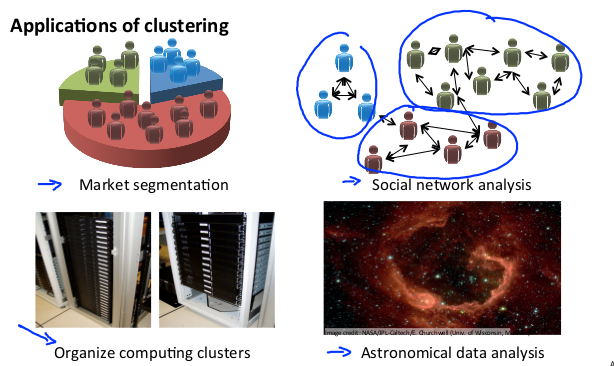
（注：这里有考题，问哪些可以使用聚类算法）

13.2 K-means算法 K-Means Algorithm

K-Means 是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。
迭代过程为：
1）选择K个随机的点，称为聚类中心(cluster centroids);
2）对于数据集中的每个数据，按照距离K个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。
3）计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置。
4）重复步骤 2-3 直至中心点不再变化。

 
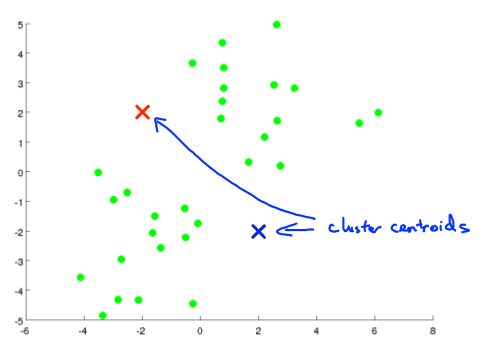
下面是一个聚类示例:

初始化随机的中心点，计算距离后分类，然后移动中心点

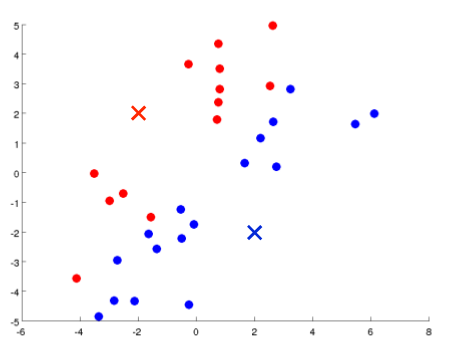
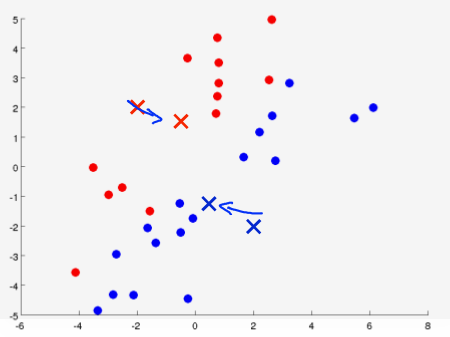
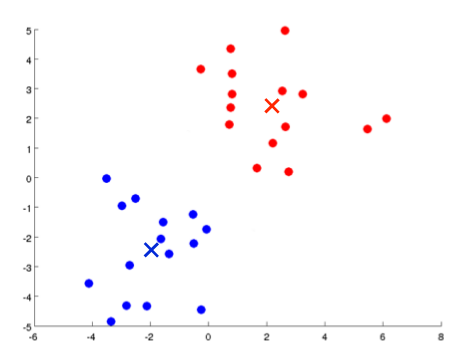
迭代很多次之后，得到最终聚类结果：

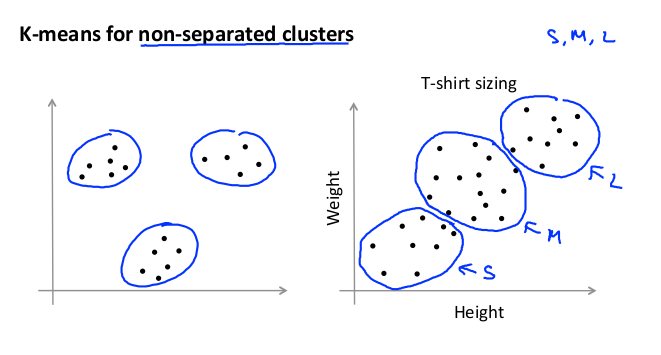
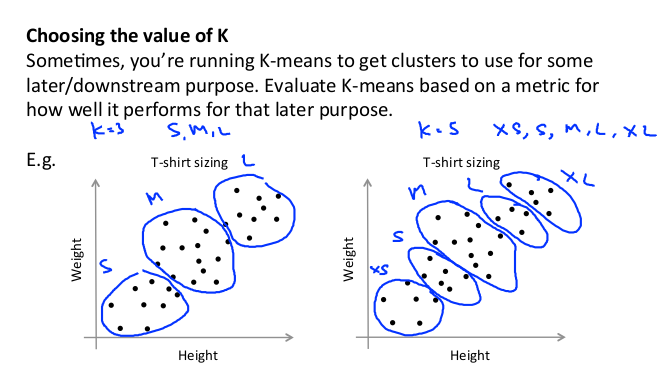
在没有非常明显组群的情况下，也可以使用K-means。例如下图中，使用K-means 确定要生产的 T-恤衫的三种尺寸：

 

 

 13.3 优化目标 Optimization Objective

 K-means最小化问题，是要最小化所有数据点与其所关联的聚类中心点之间的距离之和，因此 K-means的代价函数(又称畸变函数 Distortion function)为:

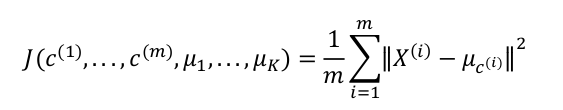
目标是使其最小

由于算法第一个循环用于减小 c⁽ⁱ⁾ 引起的代价，而第二个循环则是用于减小 μ_i 引起的代价。会在每一次迭代都减小代价，不然便说明存在错误。

 

13.4 随机初始化 Random Initialization 

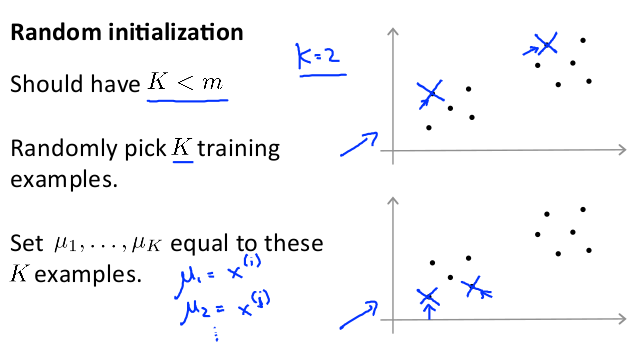
随机初始化的聚类中心点的方法：
a) 选择K < m，即聚类中心点的个数要小于所有训练集实例的数量

b) 随机选择K个训练实例，然后令K个聚类中心分别与这K个训练实例相等

 

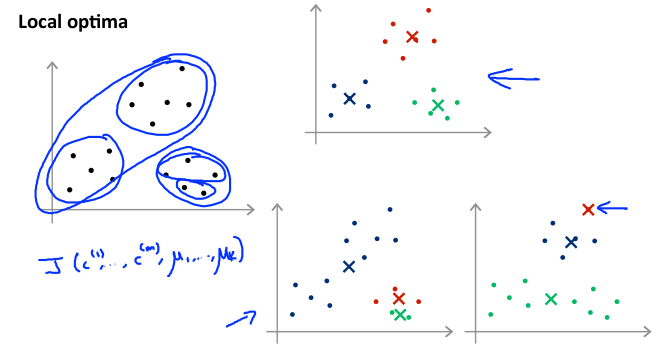
K-means的一个问题在于，如果初始化不好，有可能会停留在一个局部最小值处。通常需要运行多次 K-means算法，每一次都重新随机初始化，最后比较多次运行 K-means的结果，选择代价函数最小的结果。这种方法在K较小的时候(2-10)可行，如果K较大可能不会有明显地改善。

13.5 选择聚类数 Choosing the Number of Clusters 

没有最好的选择聚类数的方法，通常是需要根据不同的问题人工选择。需要思考运用 K-means算法的动机，然后选择能最好服务于该目的的聚类数。
这里存在一个“肘部法则”：改变聚类数K，运行聚类算法，然后计算成本函数(畸变函数)J。 有可能会得到一条类似于肘部的曲线：

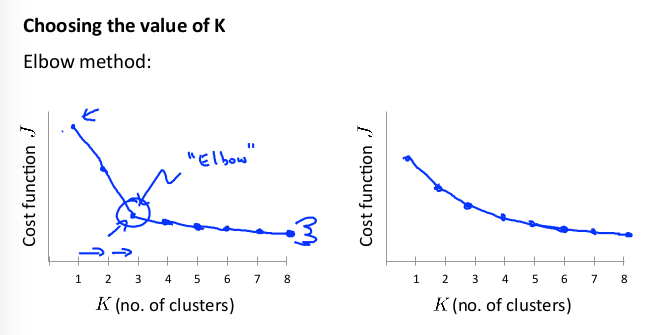
上图在 3 的时候达到一个肘点。在此之后，畸变值就下降的非常慢，那么我们就选K = 3。

但是大部分情况下图像会像右图一样没有肘点。就需要人工选择。 例如，根据客户需求选择 T-恤的尺寸数：

 

 

附，参考黄海广笔记：