【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 12—Support Vector Machines 支持向量机
Lecture 12 支持向量机 Support Vector Machines
12.1 优化目标 Optimization Objective
支持向量机(Support Vector Machine) 是一个更加强大的算法,广泛应用于工业界和学术界。与逻辑回归和神经网络相比, SVM在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。我们通过回顾逻辑回归,一步步将其修改为SVM。
首先回顾一下逻辑回归:
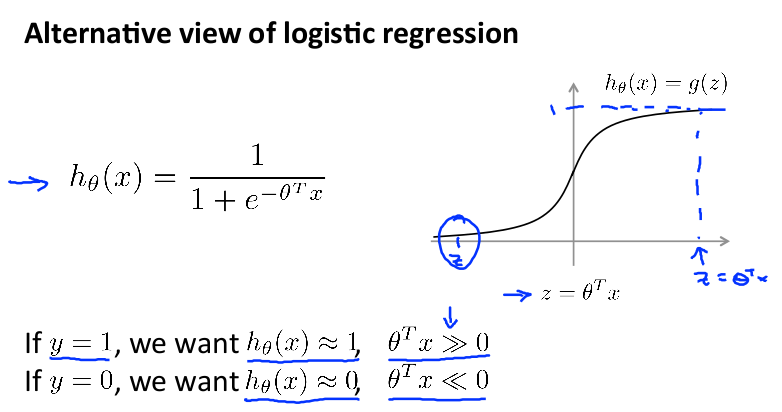
其 cost function 公式如下(这里稍微有点变化,将负号移到了括号内):
现在只考虑一个训练数据 x ,把 hθ(x)=1/(1+e-θTx) 带入公式,得到下面的式子:

下一步, 使用 z 标示其中的 θTx, 则之前的目标变为:
If y = 1, we want hθ(x) ≈ 1, z>>0;
If y = 0, we want hθ(x) ≈ 0, z<<0;
当 y = 1 或 y = 0 时, 上面逻辑回归的 cost function 分别只剩下一项, 对应下面两张图中的灰色曲线: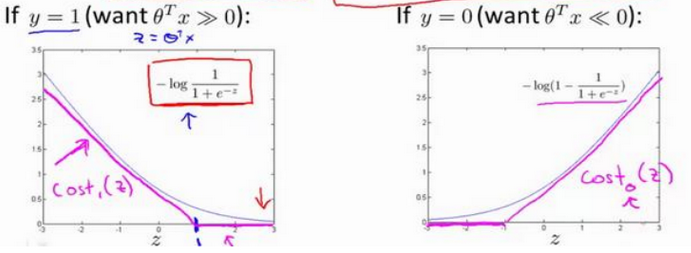
当 y=1 时,随着 z 增大,h(x)=1/(1+e-z)逼近1,cost逐渐减小。 当 y=0 时,随着 z 减小,h(x)=1/(1+e-z)逼近0,cost逐渐减小。
现在我们用新的 cost function 来代替逻辑回归中的cost function,即上图中玫瑰色的曲线,它分为直线和斜线两部分。左边的函数称为cost1(z),右边函数称为 cost0(z)。
在之后的优化问题中,这种形式的 cost function 会为 SVM 带来计算上的优势。
现在开始构建SVM

逻辑回归的 cost function 分为A、B 两个部分。 我们做下面的操作:
(a) 使用之前定义的 cost1() 和 cost0() 替换公式中对应的项。
(b) 根据 SVM 的习惯,除去 1/m 这个系数
因为1/m 仅是个常量,去掉它也会得出同样的 θ 最优值。
(c)同样根据 SVM 的习惯,做一点变动
对于逻辑回归, cost function 为 A + λ × B ,通过设置不同的 λ 达到优化目的。 对于SVM, 我们删掉 λ,引入常数 C, 将 cost function 改为 C × A + B, 通过设置不同的 C 达到优化目的。 (在优化过程中,其意义和逻辑回归是一样的。可以理解为 C = 1 / λ)
最终得到 SVM 的代价函数:

另外,逻辑回归中假设的输出是一个概率值。 而 SVM 直接预测 y = 1,还是 y = 0。
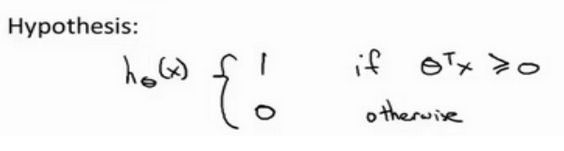
当θTx ≥ 0 时,SVM 会预测结果为1,其他情况下,预测结果为0。
12.2 大间距分类的直观理解 Large Margin Intuition
SVM 经常被看作是一个"大间距分类器",也就是找到一条与正类、负类的距离最大的分隔线。 例如下图中的黑线:

在这一节,我们将得出结论: 为了增加鲁棒性,得到更好的结果(避免欠拟合、过拟合,应对线性不可分的情况),SVM 做的不仅仅是将间距最大化,而是做了一些优化:
(1)之前的定义中,θTx ≥ 0 被分为正类,θTx < 0 被分为负类。
事实上,SVM 的要求更严格: θTx ≥ 1 被分为正类;θTx ≤ -1 被分为负类。

这就相当于在支持向量机中嵌入了一个额外的安全因子,或者说安全的间距因子。
(2)只有当C 特别大的时候, SVM 才是一个最大间隔分类器

当 C 特别大时,在优化过程中,第一项会接近于0,目标变为最小化第二项:
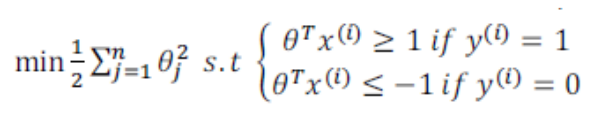
我们在训练集中加入一个异常点 outlier ,如下:
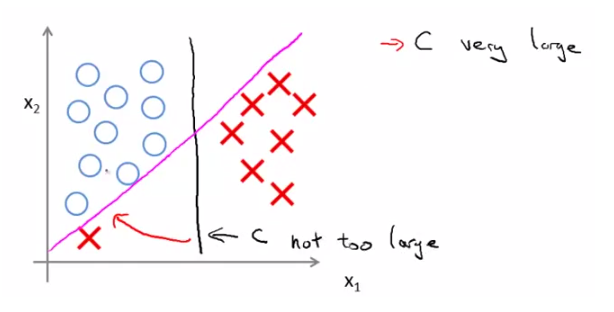
(a)如果想将样本用最大间距分开,即将 C 设置的很大。那么仅因为一个异常点,决策边界会从黑线变成那条粉线,这实在是不明智的。
(b)如果 C 设置的小一点,最终得到这条黑线。它可以忽略一些异常点的影响,而且当数据线性不可分的时候,也可以将它们恰当分开,得到更好地决策边界。
另外,因为 C = 1 / λ,因此:
C 较小时,相当于 λ 较大。可能会导致欠拟合,高偏差 variance。
C 较大时,相当于 λ 较小。可能会导致过拟合,高方差 bias。
(注:这个性质在习题中考察多次)
12.3 大间距分类背后的数学 Mathematics Behind Large Margin Classification
(1) 向量内积
先看一下向量内积的知识: 假设有两个二维向量 u 和 v ,uTv 叫做向量 u 和 v 之间的内积。
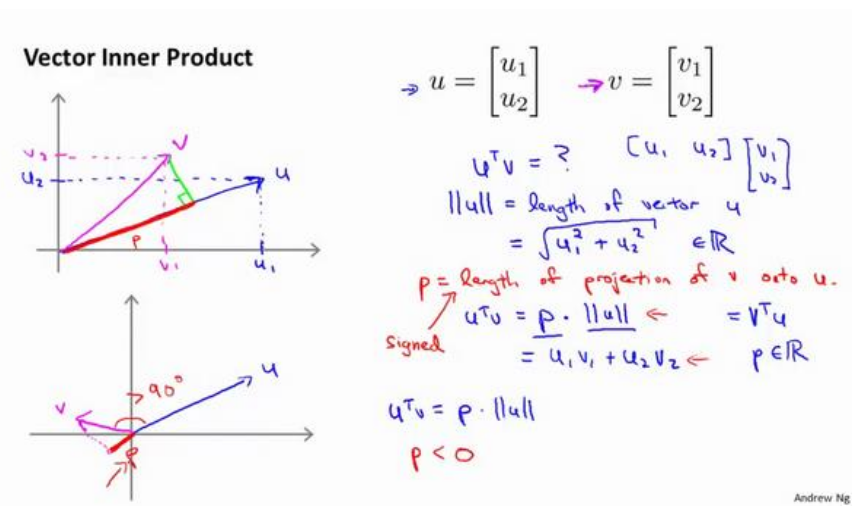
∥u∥ 表示 u 的范数norm,即向量 u 的欧几里得长度,是一个实数。根据毕达哥拉斯定理:
![]()
第一种内积计算方式:首先将 v 投影至 u 向量,记其长度为p(有正负,与u同向为正,反向为负,标量),则两向量的内积
uTv = ||u|| · ||v|| · cosθ = ||u|| · p
(注:||u|| 是一个实数,p也是一个实数,因此uTv就是两个实数正常相乘。)
第二种内积计算公式:
uTv = u1 × v1 + u2 × v2 = vTu
(2)SVM 代价函数的另一种理解
SVM的 cost function 如下:
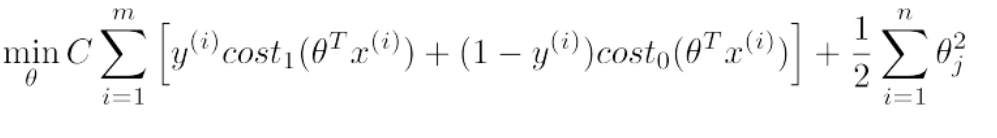
如果将C设的很大,cost function只剩下后面的那项。 为简化设 θ0 = 0,只剩下 θ1和θ2,则 cost function 为:
J(θ) = 1/2 × ||θ||^2
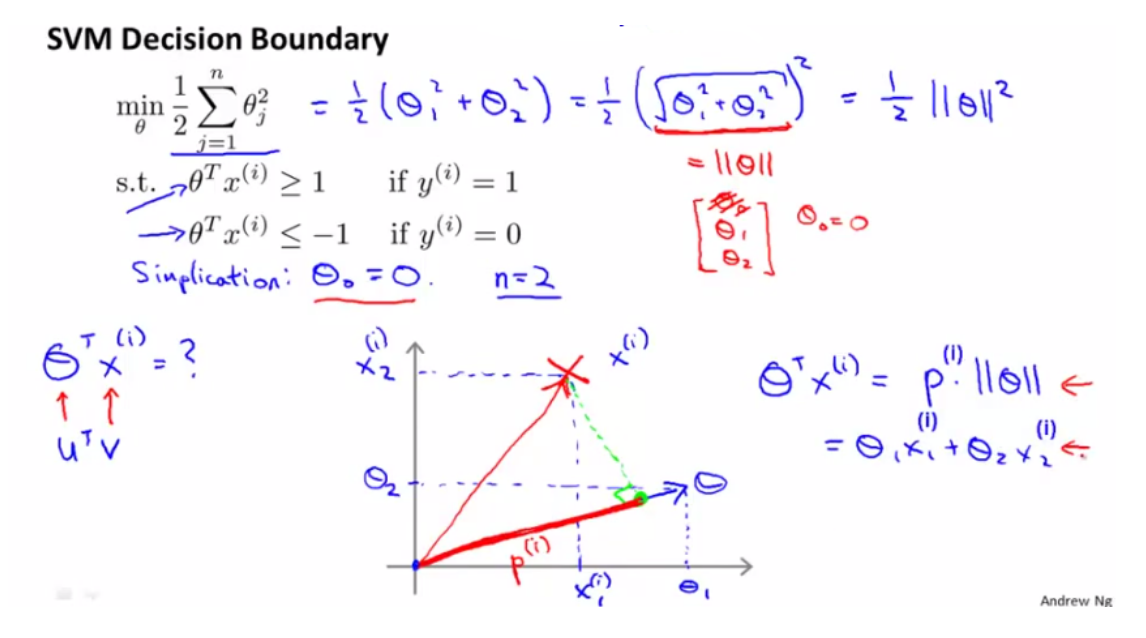
而根据上面内积的公式,我们知道有 θTx = p · ||θ||,其中 p 是 x 在 θ 上的投影。 使用p(i) ⋅ ∥θ∥ 代替之前约束中的 θTx(i) ,得到:
(3) SVM 如何选择更优的决策边界
考察优化目标函数时, 假设我们的到一条绿色的决策边界。样本在决策边界上的投影 p 是粉色的线:
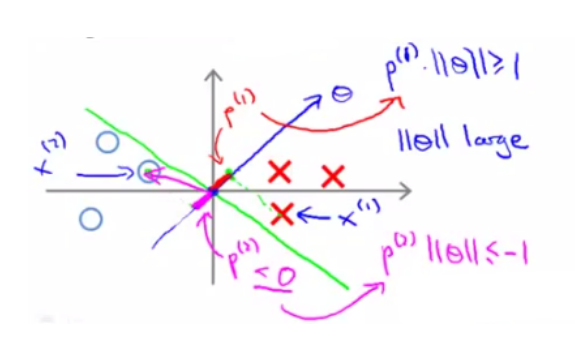
对于正样本 x(1) 而言,想要p(1) ⋅ ∥θ∥ >= 1,现在 p(1) 长度非常短,就意味着 ||θ|| 需要非常大;
对于负样本 x(2) 而言,想要p(1) ⋅∥θ∥ <= −1,现在p(2) 长度非常短,就意味着 ||θ|| 需要非常大。
但我们的目标函数是希望最小化参数 θ 的范数,因此我们希望: 投影长度 p(i) 尽可能大。例如下面这条绿色的决策边界,就更好一些:
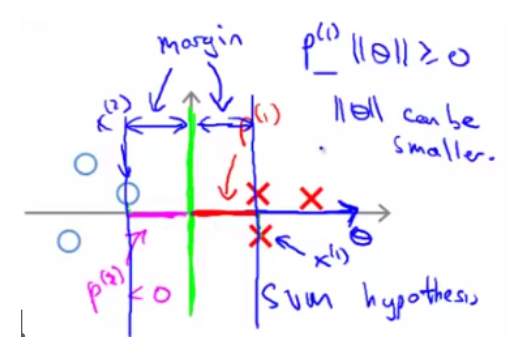
θ0 = 0的意思是我们让决策界通过原点。如果θ0 ≠ 0,决策边界不过原点 ,SVM 产生大间距分类器的结论同样成立(在 C 特别大的情况下)。
12.4 核函数 Kernels I
使用高级数的多项式模型,可以解决无法用直线进行分隔的分类:
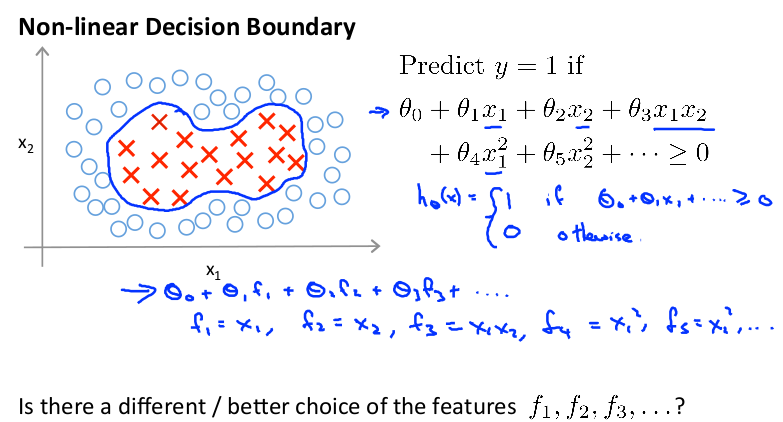
可以用一系列的新的特征 f 来替换模型中的每一项。例如令: f1 = x1 , f2 = x2 , f3 = x1 x2 , f4 = x12 , f5= x22... 得到hθ(x) = f1 + f2 +. . . +fn 。有没有更好的
方法来构造 f1 , f2 , f3 ? 我们可以利用核函数来计算出新的特征。
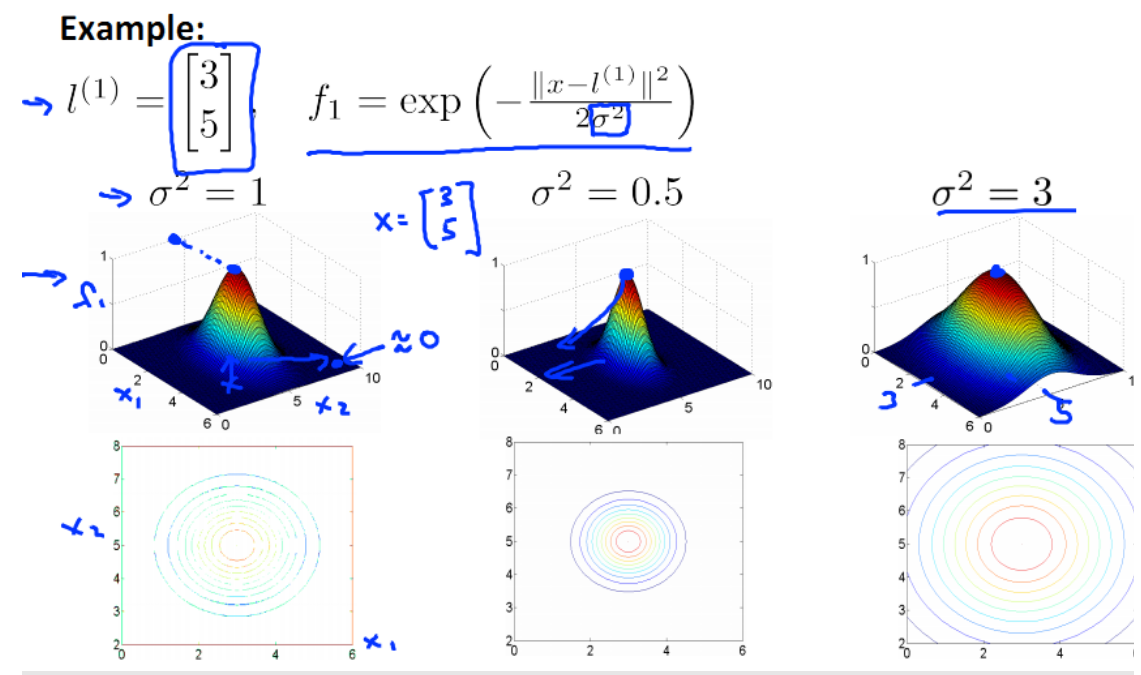
给定一个训练实例 x ,我们利用 x 的各个特征与我们预先选定的 landmarks l(1) , l(2) , l(3) 的近似程度来选取新的特征 f1 , f2 , f3 。

其中: ||x − l (1) || 为实例 x 中所有特征与 landmark l(1) 距离的和。
上例中的 similarity(x, l (1) )就是核函数,具体来说是一个高斯核函数(Gaussian Kernel)。
(注:这个函数与正态分布没什么实际上的关系,只是看上去像而已。)
如果一个训练实例 x 与 l 很近,则 f 近似于e−0 = 1;如果一个训练实例 x 与 l 很远,则 f 近似于e−( 较大的数 ) = 0。 如下:

假设 x 含有两个特征[x1 x2 ], 不同的 σ 值会有不同效果。 图中水平面的坐标为 x1, x 2 而垂直坐标轴代表 f。只有当 x 与 l(1) 重合时, f 才具有最大值。随着 x 的改变 f 值的变化速率受到 σ2 的控制。 σ2越小,曲线越瘦
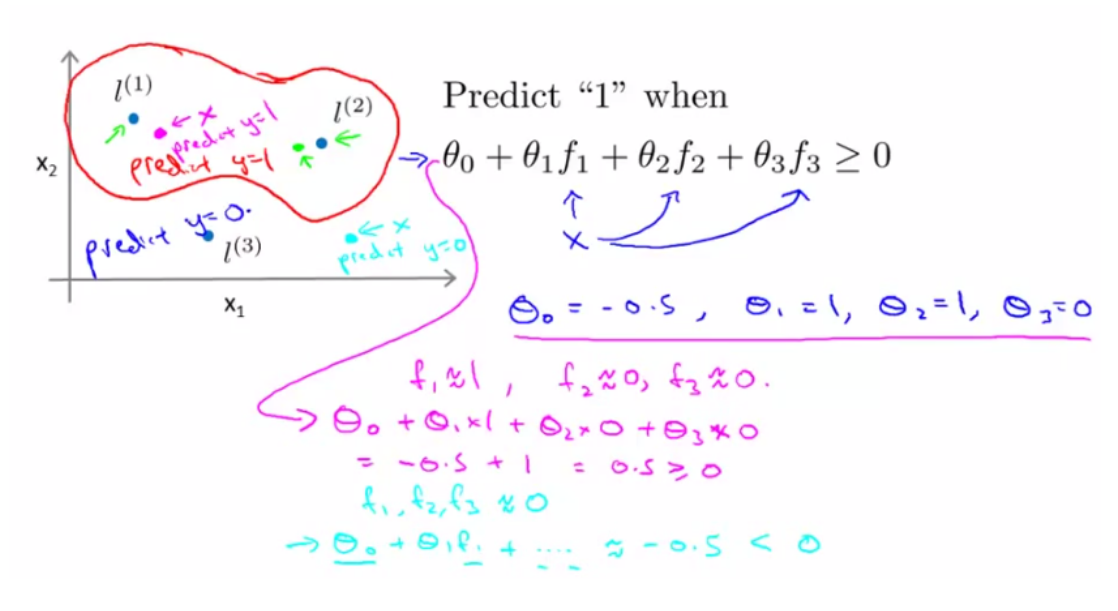
下图中,粉色点离 l (1) 更近,所以 f1 接近 1,而 f2 ,f3 接近 0。因此h θ(x) ≥ 0,因此预测y = 1;同理,绿色点离 l(2) 较近的,也预测y = 1;但蓝绿色点离三个 landmark 都较远,预测y = 0。
图中红色封闭曲线便是决策边界。在预测时我们采用的特征不是训练实例本身的特征,而是通过核函数计算出的新特征f1 , f2 , f3 。
12.5 核函数 Kernels II
(1) 如何选择 landemark
通常如果训练集有m个实例,则选取m个landmark,并将 l(i)初始化为x(i) :
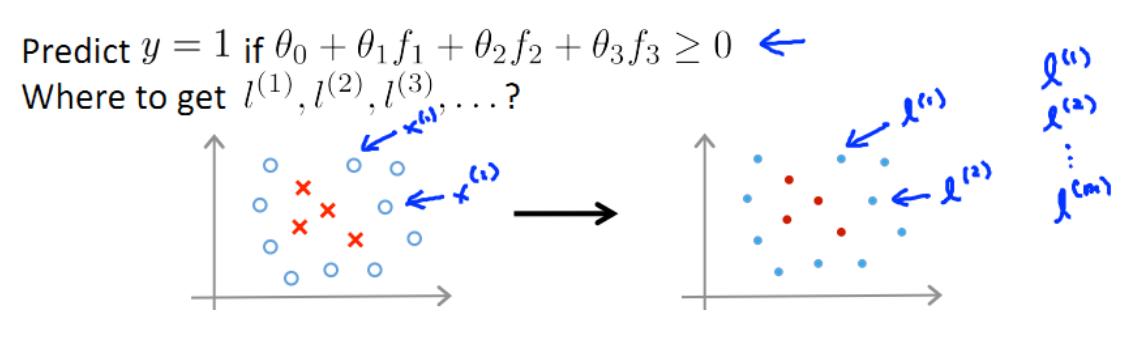
好处:新特征建立在原有特征与训练集中所有其他特征之间距离的基础之上。

对实例 (x(i),y(i)),有:
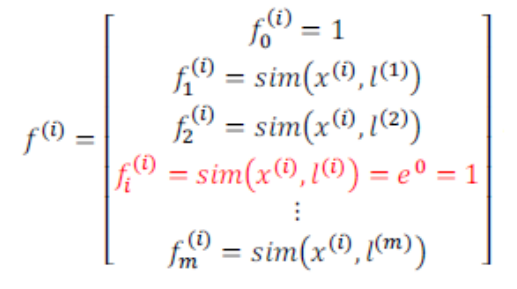 其中
其中 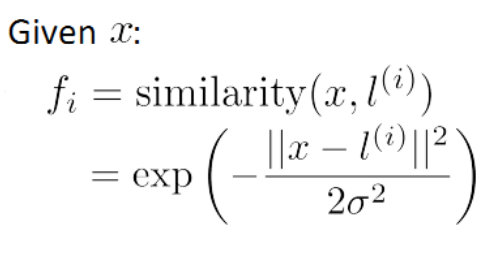
(2)将 kernel 引入 SVM
我们将Gaussian Kernel 代入 SVM 的 cost function,如下图所示:
这里与之前的 cost function的区别在于用核函数 f 代替了x。
预测一个实例 x 对应结果的方法: 给定x,计算新特征 f,当 θTf >= 0 时预测 y = 1; 否则反之。
(3)简化计算
最后,为了简化计算, 在计算正则项 θTθ 时,用 θTMθ 代替 θTθ ,其中 M 是一个矩阵,核函数不同则M不同。
(注:理论上也可以在逻辑回归中使用核函数,但使用 M 简化计算的方法不适用于逻辑回归,计算将非常耗时。)
(4)线性核函数
不使用核函数又称为线性核函数(linear kernel)。线性核函数SVM 适用于函数简单,或特征非常多而实例非常少的情况。
(5)SVM 的参数
带有 kernel 的 SVM 有两个参数 C 和 σ,对结果的影响如下:
1. C
当 C 较大,相当于 λ 小,可能会导致过拟合,高方差 variance;
当 C 较小,相当于 λ 大,可能会导致欠拟合,高偏差 bias;
2. σ
当 σ 较大时,图像扁平,可能会导致低方差,高偏差 bias;
当 σ 较小时,图像窄尖,可能会导致低偏差,高方差 variance。

12.6 使用支持向量机 Using An SVM

(1)使用现有软件包
我们通常需要自己写核函数,然后使用现有的软件包(如 liblinear,libsvm 等) 来最小化 SVM 代价函数。强烈建议使用高优化软件库中的一个,而不是尝试自己实现。
(2)对比一下两种 SVM
一种是No kernel(linear kernel),hθ(x)=g(θ0x0+θ1x1+…+θnxn),predict y=1 if θTx>=0;
另一种是使用kernel f(比如Gaussian Kernel),hθ(x)=g(θ0f0+θ1f1+…+θnfn),这里需要选择方差参数σ2
(3)特征缩放
特别地,如果使用高斯核函数,需要进行特征缩放。

(4)其他 kernel
在高斯核函数之外,还有其他一些选择,如:
多项式核函数(Polynomial Kernel), 字符串核函数(String kernel), 卡方核函数( chi-square kernel) ,直方图交集核函数(histogram intersection kernel) 等。
它们的目标也都是根据训练集和地标之间的距离来构建新特征。一个核函数需要满足 Mercer's 定理,才能被 SVM 的优化软件正确处理。 但是Andrew表示他不用其他kernel函数。

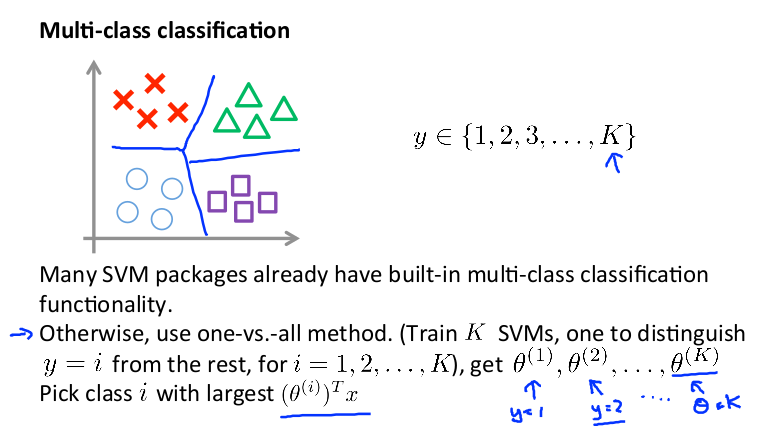
(5)多分类问题
可以训练k个支持向量机来解决多类分类问题。 但是大多数支持向量机软件包都有内置的多类分类功能,我们只要直接使用即可。
(6) 参数设置
尽管有现成的库,但是我们也需要做几件事:
1、参数C的选择。
2、选择内核参数或你想要使用的相似函数 (注:如果选择不需要任何内核参数,还称为使用了线性核函数 SVM。)
(7)逻辑回归模型 和 SVM 的选择
下面是一些普遍使用的准则:
n为特征数,m为训练样本数。
(a) 如果 n » m,即训练集数据量不够支持我们训练一个复杂的非线性模型,选用逻辑回归模型或者不带核函数的 SVM。
(b) 如果 n较小,m中等,例如n在 1-1000 之间,而m在 10-10000 之间,使用高斯核函数的 SVM。
(c) 如果 n较小,m较大,例如n在 1-1000 之间,而m大于 50000,则使用 SVM 会非常慢。解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的 SVM。
如果训练集非常大,高斯核函数的SVM 会非常慢。 通常Andrew会尝试手动创建特征,然后用逻辑回归或者不带核函数的 SVM。
(注: 逻辑回归和不带核函数的SVM 非常相似。但是根据实际情况,其中一个可能会更有效。随着 SVM 的复杂度增加、特征数量相当大时,不带核函数的SVM 就会表现得相当突出。)

一个设计得很好的神经网络也很有可能会非常有效。有一个缺点是,可能会特别慢。一个非常好的 SVM 实现包可能会运行得比较快比神经网络快很多,而且它的代价函数是凸函数,不存在局部最优解。 (黄海广注:当时 GPU 计算比较慢,神经网络还不流行。)


