【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 10—Advice for applying machine learning 机器学习应用建议
Lecture 10—Advice for applying machine learning
10.1 如何调试一个机器学习算法?
有多种方案:
1、获得更多训练数据;2、尝试更少特征;3、尝试更多特征;4、尝试添加多项式特征;5、减小 λ;6、增大 λ

为了避免一个方案一个方案的尝试,可以通过评估机器学习算法的性能,来进行调试。
机器学习诊断法 Machine learning diagnostic 的定义:

10.2 评估一个假设
想要评估一个算法是否过拟合

(一)首先,划分测试集和训练集
如果数据已经随机分布了, 可以选择前70%数据作为训练集,剩下的30%作为测试集;
如果数据不是随机分布的,最好先打乱,或者随机选择70%数据作为训练集,剩下的30%作为测试集

(二)然后,计算测试误差
1、对于回归问题。例如线性回归。首先使用训练集进行训练,然后使用测试集计算测试误差:

2、对于分类问题。例如逻辑回归,也是一样的:

有一种更易理解的测试误差定义方式,叫做 错分率 Misclassification error (也叫0/1错分率):

err(hθ(x),y) 的意思是:如果分类预测结果 hθ(x) 错误,则 err 值为1;如果 hθ(x) 预测正确,则 err 值为0。 整体的测试误差就是所有 err 值的加和。
10.3 模型选择 和 "训练/验证/测试"集
产生过拟合的一个原因是:仅仅在测试集合上调试 θ 得到的训练误差,通常不能作为对实际泛化误差的一个好的估测。

那么究竟应该选择几次多项式来作为我们的模型呢?
假设针对 x 有10个模型:一次方程 直到 十次方程。对每个多项式,在训练集上训练出 θ 。然后分别使用 test 集合计算误差,分别得到 Jtest(θ(1)),...Jtest(θ(10)),发现 Jtest(θ(5))的值最小,因此选择 d=5 这个模型。
但这里有个问题:我们选的这个模型,就是能够最好地拟合测试集的参数d的值及多项式的度。因此,再使用同样的测试集来评价假设,显然很不公平,很可能导致过拟合。
所以,我们改为将数据集分为 6:2:2 三部分:training set、cross validation set(cv, 或者直接简称validation set)、test set
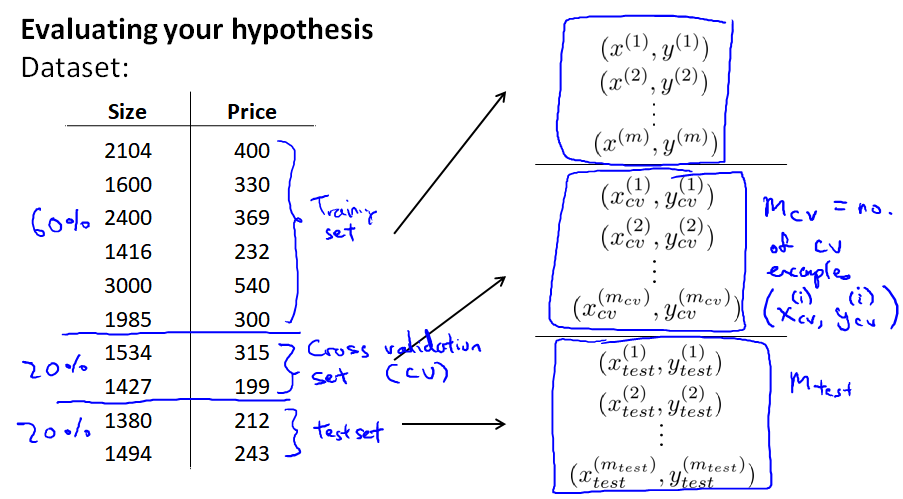
每个集合上的误差计算公式:

现在我们是用 cv 集合计算误差,分别得到 Jcv(θ(1)),...Jcv(θ(10)),发现 Jcv(θ(4)) 的值最小,因此选择 d=4 这个模型,最后在 test 集合上进行预测,能得到一个更理想的泛化误差。

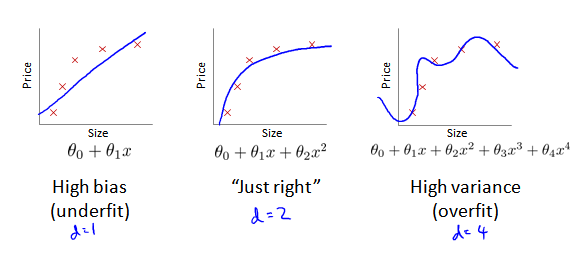
10.4 检验误差和方差 Diagnosing bias vs. variance
模型表现不好,通常有两种情况:
(1) 误差 bias 过大,导致欠拟合 underfitting;
(2) 方差 variance 过大,导致过拟合 overfitting
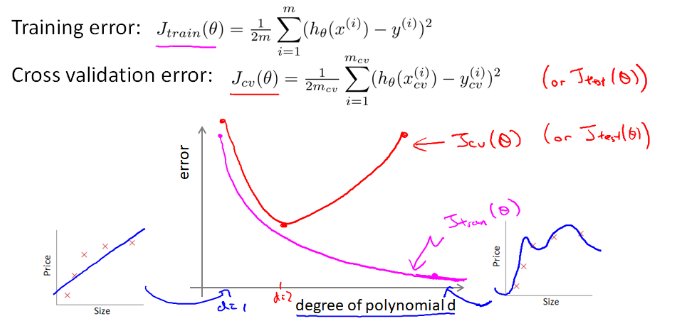
使用多项式的度 d 作为横轴,在训练集和cv集上分别计算 J(θ),得到曲线:
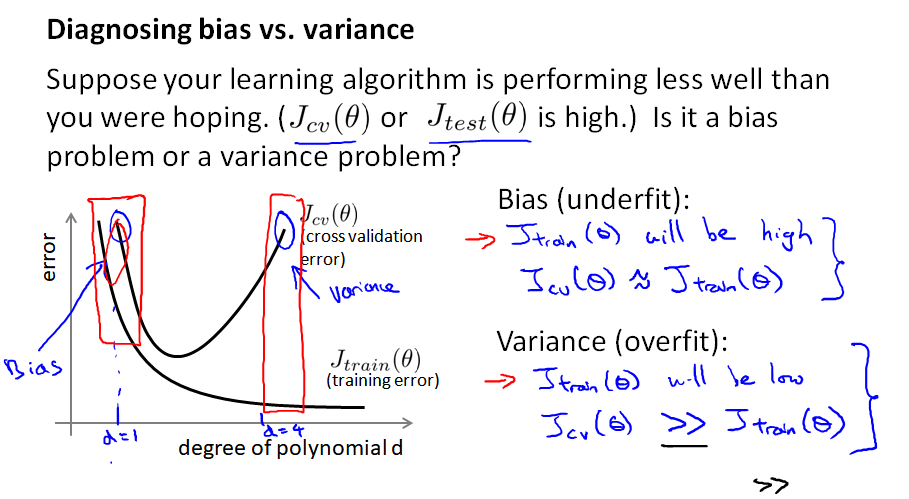
下面说如何根据两条曲线判断模型是高误差(欠拟合)、还是高方差(过拟合)。
(1) 先看曲线左边,当 d=1 ,训练集和cv集的误差都很大,说明欠拟合
(2) 再看曲线右边,当 d=4 ,训练集误差很小、cv集误差远大于训练误差,说明在训练集上过拟合
10.5 正规化 和 偏差/方差
考虑正则化的线性回归模型:
(1) 当 λ 过大,θ 被惩罚后会变得很小、接近于0,最后方程只剩下 θ0 这一项,成为一条直线,导致高偏差bias、欠拟合。
(2) 当 λ 过小,正则项不起作用,导致高方差 variance、过拟合。
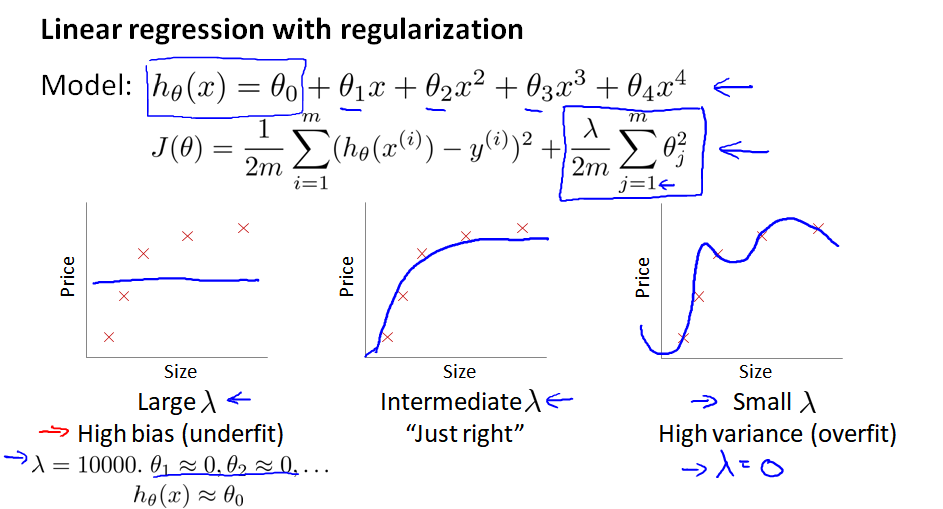
那怎么选择 λ 的值呢?
首先,当我们定义每个集合上的误差函数时,不考虑 λ。
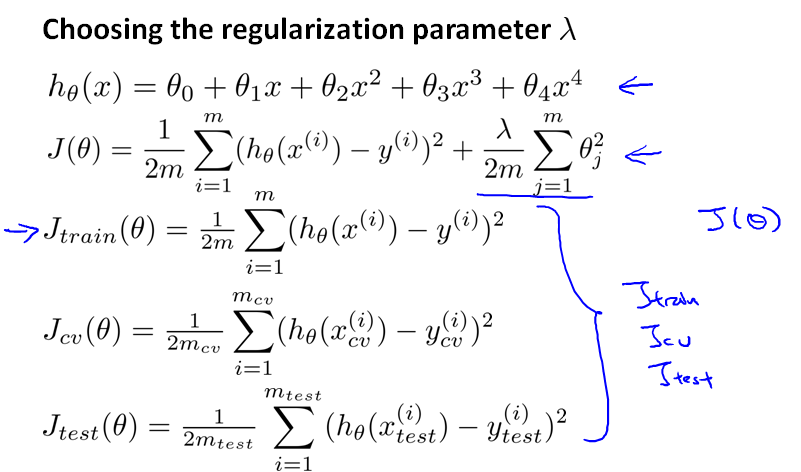
然后按照步长两倍的方式递增 λ,针对每个 λ 训练θ。然后分别计算对应的Jcv(θ),得到最小的Jcv(θ(5))。然后在 test 集合上进行测试。

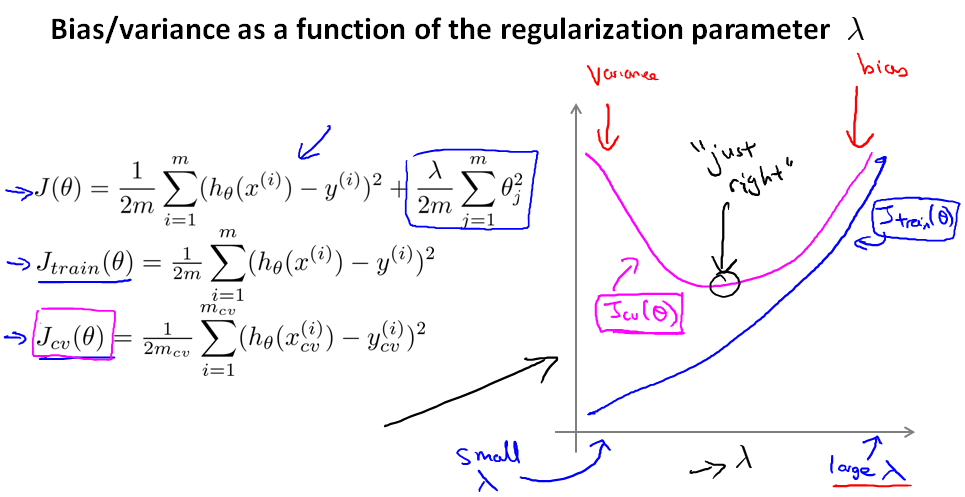
现在我们看一下,λ 的大小对损失函数的影响。
(1) 先看曲线左边,当 λ 很小 ,Jcv(θ) 的值远大于 Jtrain(θ),说明过拟合
(2) 再看曲线右边,当 λ 很大 ,Jcv(θ) 和 Jtrain(θ) 都很大,说明欠拟合
10.6 学习曲线
m指训练样本的个数,曲线显示不同的m对于J(θ)的影响
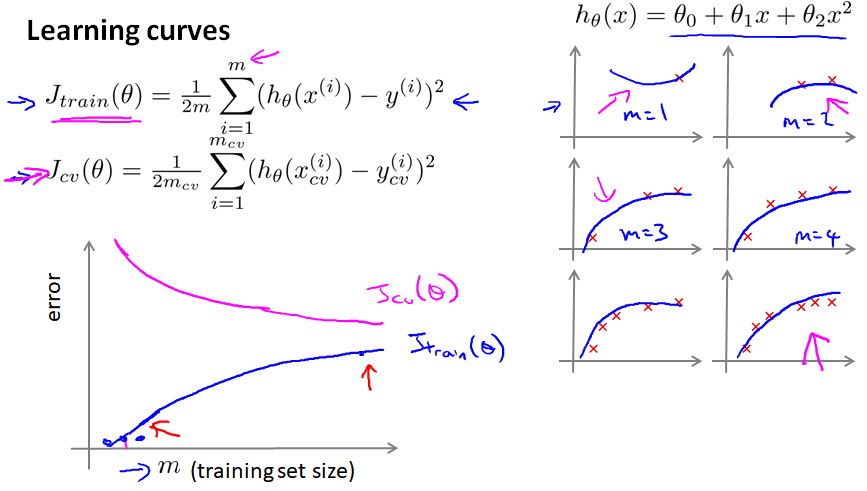
高偏差 bias、欠拟合:

高方差 variance、过拟合。两个曲线会有一个很大的gap:

10.7 接下来
每种解决方案对应的问题如下(箭头右侧指向的是表现出的问题,左侧是解决方案):

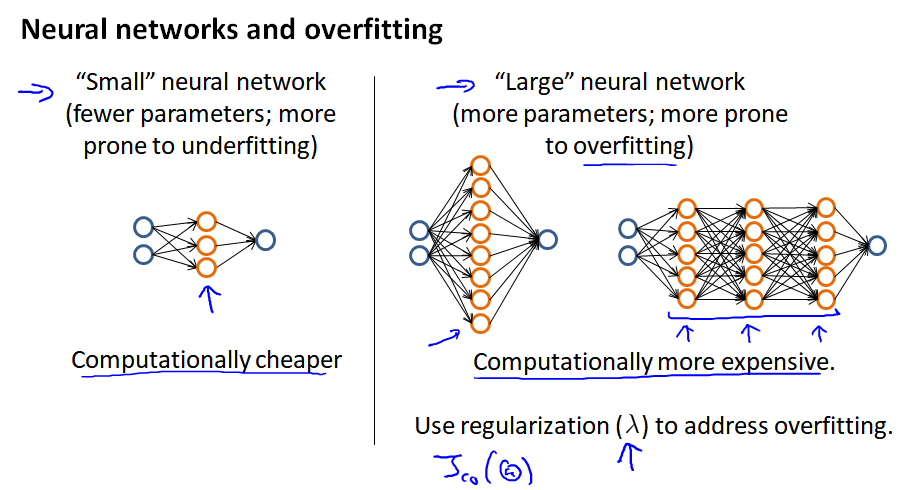
对于神经网络,开始可以尝试一个相对比较简单的神经网络模型,计算量小。
如果使用大型神经网络,使用正则化来修正过拟合。
如果不知道选择几层hidden layer,可以将数据分为三个数据集之后,分别做测试。
附
关于偏差和方差的解释,参考:https://blog.csdn.net/u010626937/article/details/74435109
偏差:描述的是预测值的期望与真实值之间的差距。偏差越大,越偏离真实数据集。(Ps:假设靶心是最适合给定数据的模型,离靶心越远,我们的预测就越糟糕)
方差:描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,预测结果数据的分布越散。
基于偏差的误差:所谓基于偏差的误差是我们模型预期的预测与我们将要预测的真实值之间的差值。偏差是用来衡量我们的模型的预测同真实值的差异。
基于方差的误差:基于方差的误差描述了一个模型对给定的数据进行预测的可变性。比如,当你多次重复构建完整模型的进程时,方差是在预测模型的不同关系间变化的多少。
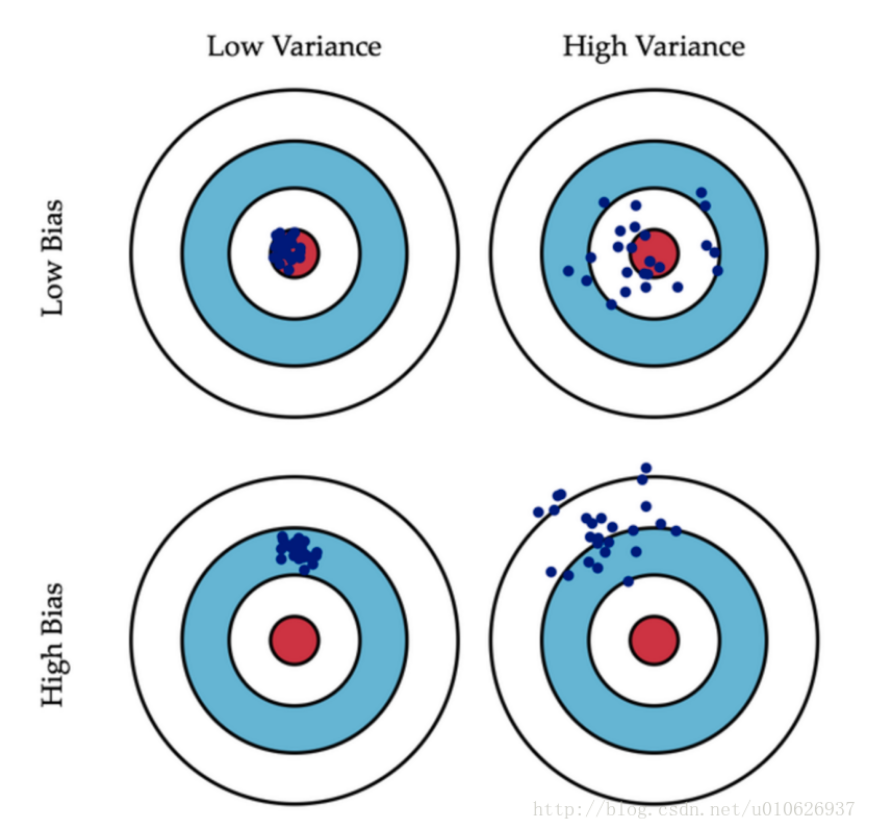
左上:低偏差bias,低方差variance。预测结果准确率很高,并且模型比较健壮(稳定),预测结果高度集中。
右上:低偏差bias,高方差variance。预测结果准确率较高,但是模型不稳定,预测结果比较发散。
左下:高偏差bias,低方差variance。预测结果准确率较低,但是模型稳定,预测结果比较集中。
右下:高偏差bias,高方差variance。预测结果准确率较低,并且模型不稳定,预测结果比较发散。


