Codeforces Round #360 D

Remainders Game

题意：给你一个k，给你n个数ci，并且你知道x%ci的值（没有给出），问能否确定是否存在唯一的x%k

思路：由中国剩余定理可知道    （mi相当与题目给的ci，M是mi的乘积，Mi=M/mi，ti是Mi的逆元）

 

     

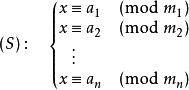
但是中国剩余定理要求mi互质，但是题目中给的ci是不一定互质的，但是可知列出同余方程组后，可以得最小正整数解为x，通解为x+p*M（M在中国剩余定理是mi的乘积，但是在这里是所有mi的LCM，其实在中国剩余定理里也是LCM），因为是求x%k是否有唯一解，则列出x的通解%k的方程组     x%k=y1    (x+M)k=y2 ..........(x+pM)%k=yp，若存在唯一解，说明y1=y2=...=yp，即方程组两两同余，根据同余可推得任意2个式子相减 -> (x+M)%k -x%k = 0； 即pM%k=0（p可以为大于1的任意数），即M%k=0；所以，若M%k=0，即存在唯一解

 

AC代码：

#include "iostream"
#include "string.h"
#include "stack"
#include "queue"
#include "string"
#include "vector"
#include "set"
#include "map"
#include "algorithm"
#include "stdio.h"
#include "math.h"
#pragma comment(linker, "/STACK:102400000,102400000")
#define ll long long
#define bug(x) cout<<x<<" "<<"UUUUU"<<endl;
#define mem(a,x) memset(a,x,sizeof(a))
#define mp(x,y) make_pair(x,y)
#define pb(x) push_back(x)
#define lrt (rt<<1)
#define rrt (rt<<1|1)
using namespace std;
const long long INF = 1e18+1LL;
const int inf = 1e9+1e8;
const int N=1e5+100;
const ll mod=1e9+7;

///DDDD
ll n,k,c,f=1;
int main(){
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>k;
    for(int i=1; i<=n; ++i){
        cin>>c;
        f=f/__gcd(f,c)*c;
        f%=k;
        if(f==0){
            cout<<"Yes\n";
            return 0;
        }
    }
    cout<<"No\n";
    return 0;
}