密码学之前后向安全性
本文将讨论密码学中的 前向安全性(Forward Security) 与 后向安全性(Backward Security) ,希望读完本文后,你再也不会混淆这两个概念。
在开始本文之前,希望你有如下预备知识:
- 密码学(Cryptography)是一门什么样的学科?
- 单向函数(One Way Function)是什么?有哪些例子?
- 密码算法与密钥是什么?敌手(Adversary)在密码学中是一个怎样的概念?
单向函数与密码算法
现代密码学的基石:伪随机性
Pseudorandomness,即伪随机性,是一个现代密码算法必须要具备的性质,因为从反面考虑,如果你设计的密码算法都做不到「看起来」是随机的,那岂不是很容易就被攻破了?当然,伪随机性在数学上有着更严格的定义与论证,在密码学中也有更深厚的历史背景(比如其实是姚期智院士率先给出的伪随机性正式定义[1])。伪随机作为现代密码学的核心要素,如何更好地实现它一直是许多科学家追逐的目标,比如采用物理的随机熵源(真随机数发生器),或者使用一个秘密的随机种子(密钥)等等。没有伪随机性作为算法的根基,Rivest也不能打包票对你说“哦我的老伙计,试试这个RSA吧,它真的很棒”。
在现代密码算法中,伪随机性可以由伪随机数发生器(PseudoRandom Number Generator,PRNG)来提供。这就是说,要设计一个具备伪随机性的密码算法,你可以先明确怎么得到一个PRNG。因此,PRNG这个部件的好坏,将直接决定了算法是否足够安全。PRNG在现代密码学语义中的定义如下:
令$G$为一多项式时间算法,其输入为$s\in \{0, 1\}^{n}$,即为一长度为$n$的01比特串,输出的长度记作$l(n)$;其中,$l(\cdot )$也为一多项式时间算法,但与$G$不同的是,$l(n)$只是表示是$n$的多项式界下的一个值,$l(\cdot )$可以等于$n^{2}$,也可以等于$n$,只要是多项式界内的即可。若G为一PRNG,则应同时满足如下两个条件:
- 对于任意的$n$,都有$l(n) > n$;
- 若此时对于任意一具有多项式资源的敌手$\mathcal{A}$,都存在一个可忽略(negligible)的概率$\epsilon $,使得下式成立:
$$ |\mathrm{Pr}[\mathcal{A}(r)=1] - \mathrm{Pr}[\mathcal{A}(G(s))=1]| \le \epsilon $$
其中,$r$为一真随机比特串(不用管它从哪来的),而$G(s)$即为$G$的输出,为一伪随机比特串. 而$\mathcal{A}(r)=1$与$\mathcal{A}(G(s))=1$分别表示敌手$\mathcal{A}$能正确判断出所给比特串是真随机串还是伪随机串。因此,条件2表明敌手$\mathcal{A}$面对$G$的输出时,只能以一个可忽略的、极小的概率将其与真随机串区分开来,这保证了每个PRNG的输出都会足够贴近真实的随机输出。而对于条件1,如果我们先假设$l(n) \le n$,那这意味着输入与输出都不一定能满足双射的条件,即PRNG的一个输出甚至可能对应着多个输入。由此,这样的PRNG很容易就被攻击者猜解碰撞出来了;因此如果令$l(n) > n$,如$l(n)=2n$,那么一个输入$s$则平均对应着$2^{n}=2^{2n}/2^{n}$个PRNG输出,也就是这是一种非常稀疏的映射关系,这种「扩展性」保证了采取穷举手段从PRNG的输出空间来进行碰撞是困难的。
现在我们有了伪随机性这把(简陋)的螺丝刀,还能造出更好的工具吗?
单向函数
首先便是直接由伪随机性抽象而来的、更加直观的,但也非常重要的性质:One-Wayness,即单向性。顾名思义,再结合PRNG的定义,相信大家此时对单向性及单向函数(One-Wayness Function, OWF)也会有这样一个模糊理解:
给函数一个$x$,可以跟容易算出对应的函数值$y$,但是对于函数值$y$,很难逆推得到原来的$x$
这种理解其实已经非常接近单向函数的正式定义了,如下所示:
一个函数f若称为单向函数,则应满足如下两个条件:
- (容易计算)存在一多项式时间算法$A_{f}(\cdot )$,对于任意输入$x \in \{0, 1\}^{*}$,都能在多项式时间内输出$A_{f}(x)=f(x)$;
- (难以求逆)对于所有的多项式时间算法$D(\cdot )$,都存在一个极小的可忽略概率$\epsilon$,使得下式成立:
$$ Pr[D(f(x)) \in f^{-1}(f(x))] \le \epsilon $$
其中,$x$的选取是从$\{0,1\}^{n}$中随机均匀采样。在上述定义中,难以求逆这一性质只需要在输入是均匀选取的这一条件下成立即可,即对于极个别的输出点,攻击者还是有可能还原其对应的输入的。在某些比较极端的定义里,难以求逆这一性质甚至只要求在输入$x$足够长时才满足。
此时你可能会说,既然一个单向函数是容易计算的,那对于一个特定的输出$y$,那我为什么不能试着遍历所有$x_{i}$,从而找到$f(x^{*})=y$?没错,任何单向函数在给出足够时间和计算资源的条件下,都是可求逆的;但不要忘记条件2中面向的是多项式时间算法,对于那些指更高级的攻击算法,单向函数可能真的一下就被攻破了。因此,条件2所谓的难以求逆,实际上是难以「高效」求逆。
实际上,任意一个PRNG都可看作是一个单向函数 [2],而要证明这一点,即证「对于一个PRNG算法 $\mathcal{G}$,如果存在敌手$\mathcal{D}$能以不可忽略的概率对 $\mathcal{G}$的输出结果求逆,那么存在一敌手$\mathcal{D}^{'}$也能以不可忽略的概率分辨$\mathcal{G}$的输出与真随机串。一般而言这种证明采取“安全性归约”的方法即可,不过这和本文内容无关。总之,基于PRNG可以构造出单向函数,而有了单向函数这个「高级扳手」,我们就可以造出更方便的工具了,比如大名鼎鼎的(密码学安全的)哈希函数。
阿克琉斯之踵:密钥的管理
PRNG与OWF由于其简洁但重要的计算性质,常被用于生成密码算法的密钥,而PRNG这种「看起来」随机的特点,正是方便我们生成一些别人不想预测出的敏感信息。另外,OWF则能帮助我们为已有密钥提供一个「陷门」(Trapdoor),陷门的输出(通常为OWF的输出)可以作为新密钥、或者某个公开值,或者某个校验值等等。
二者的配合让一个系统中,密钥的在线更新成为了可能。如果一个OWF提供的伪随机性足够好,那我们是不是可以用它源源不断地生成新密钥呢?当然可以!
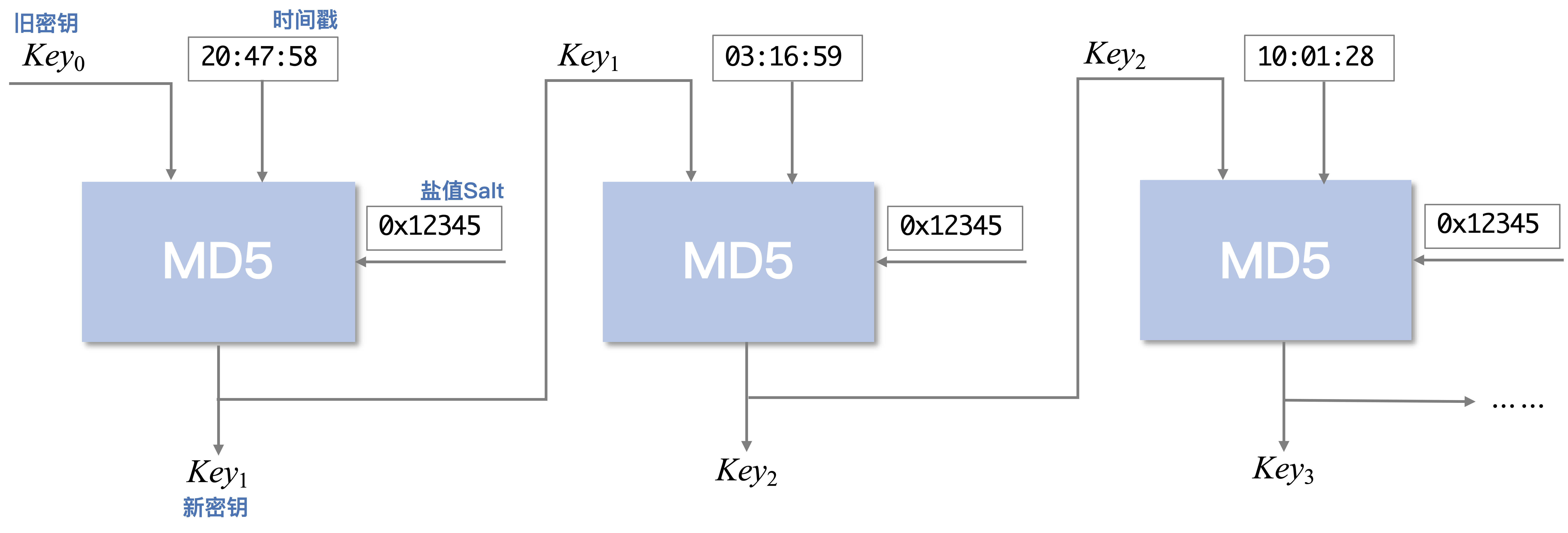
如上图所示,系统管理员可以使用当前密钥$K_{i}$、当前时间戳$t_{i}$以及一个盐值Salt(如0x12345),在MD5这一哈希函数的帮助下源源不断的迭代出新密钥$k_{i + 1} = \mathrm{MD5}( K_{i} || t_{I} || Salt) $。当然,MD5可以替换为其他常见的,更安全的哈希函数。
可是,随着密码分析技术的不断增强,原来认为安全的MD5目前来看也不那么安全了,原本的单向函数也不再那么单向了。而管理员此时还觉得:
反正我密钥一直都在给你们更新,况且MD5也没那么容易被攻击,这个方案又不是不能用😄
管理员笑了,黑客也笑了。

这种做法有一个无法忽视的风险在于,如果系统中某些用户喜新厌旧,他只会好好保管手头上的新密钥,那么若攻击者获取了他曾经的密钥,目前的系统还是安全的吗?另外,如果攻击者获取了他目前的密钥,系统中的历史状态还会是安全的吗?
这样的密钥管理问题一直是许多密码学专家的心头之恨:“明明这算法本身已经天衣无缝了,攻击者还是能从一些奇怪的地方拿到密钥”,而根据Kerkoff准则,一旦密钥不安全了,那整个密码系统也就不安全了。因此,密钥管理就像是一个信息系统的阿克琉斯之踵一样,只要攻击者拥有足够精妙的攻击方法,他便能一击致命。
前向安全性 与 后向安全性
铺垫了那么多,终于要介绍正题了。
直觉上的判断
如果你直接Google "Forward/Backward Security",你很可能会看到两种截然相反的定义:
版本一[3]:
- 前 向安全性是指,当前密钥被攻击者获取后,历史 的密钥仍然是安全的
- 后 向安全性是指,当前密钥被攻击者获取后,未来 的密钥仍然是安全的
版本二[4]:
- 前 向安全性是指,当前密钥被攻击者获取后,未来 的密钥仍然是安全的
- 后 向安全性是指,当前密钥被攻击者获取后,历史 的密钥仍然是安全的
直觉上理解,可能有的读者在看到「前向」一词时,脑海里自然而然会浮现出一根时间轴,前向安全性似乎在告诉你,如果当前时间点的密钥泄露了,之“前”走过的所有密钥节点都还是安全的。这样一来,前向安全性就是说历史密钥是安全的,而后向安全性自然就是未来密钥是安全的嘛(版本一)
诚然,有的读者可能是这么理解的:前向安全性的英文是Forward Security,而后向是Backward;而直觉上当你看到「Backward」一词时,脑海里同样会浮现出一根时间轴,这个词似乎在告诉你,如果当前时间点的密钥泄露了,那么往“回”(Backward)走的所有密钥节点都还是安全的。这样一来,后向安全性就是说历史密钥仍是安全的,而前向安全性自然就是未来密钥仍是安全的嘛(即版本二)
说实话,我自己的直觉理解是版本二,但实际上,目前学术界公认的正确定义其实是版本一。
如何理解
可能和我一样认为版本二是正确的读者不是很能理解版本一中的 前(Forward)与后(Backward) 究竟指的是何处的 前与后,明明让Backward对应“曾经”,Forward对应“未来”就很通顺嘛。其实这种对应关系本身在语义逻辑上并没有问题,只是在密码学家看来,二者并非这么去理解。
在版本二的错误定义中,Forward 与 Backward 被理解为在当前密钥泄露之后,哪个时刻是否还是安全的?即 前与后 修饰的其实是 结果时刻 相对于 密钥泄露的发生时刻,如下图所示。

而在版本一的正确的定义中,Forward 与 Backward 被理解为哪个时刻的密钥被泄露了,目前是否还是安全的?即 前与后 修饰的其实是 密钥泄露的发生时刻 相对于 结果时刻 ,如下图所示。

因此,在两种版本的理解中,Forward与Backward的方向是相反的(如图中的虚线箭头),而至于为什么版本一是正确的,而版本二并不太被接受呢?因为正确定义刻画的是当系统从正常状态,逐渐转移到不正常状态(密钥被泄露了)的过程中,安全性的变化;即错误定义虽然看起来更符合人们的思考逻辑,即面对着当前不正常的系统状态,那些正常的系统状态中安全性如何。然而正确定义更能描述清楚系统安全性的演化过程,这比单纯符合人们思考第一印象来的要更为「学术化」一些。
总结一下吧
前后向安全性是很多密码方案都会考虑的一个安全目标,例如密钥协商、可搜索加密等等。本文对这一概念重新进行了梳理,也讨论了两种版本定义该如何去理解。最后,如果大家懒得看这么多,可以按照“前”是以“前”还安全,“后”是以“后”还安全,这样去记就好。
啰嗦了这些,其实本质上只是文字游戏罢了,而且两个版本的定义并不存在绝对的正确与错误,有些专业论文也都在混用。读者还是要把握前后向安全性的精髓,以及这两个定义究竟有什么意义,这才是最为重要的。
感谢你的阅读,最后同样以一句歌词作为结束。
“十年之前你不认识我,我不属于你,我们还是一样” —— 林夕《十年》
参考
[1] https://www.di.ens.fr/users/phan/secuproofs/yao82.pdf
[2] https://crypto.stackexchange.com/questions/41140/is-every-pseudorandom-generator-a-one-way-function
[3] https://en.wikipedia.org/wiki/Forward_secrecy
[4] https://users.ece.cmu.edu/~adrian/projects/sec/node6.html
其他参考阅读
https://crypto.stackexchange.com/questions/39761/definitions-of-secrecy
https://www.zhihu.com/question/45203206
https://www.quora.com/What-is-exactly-backward-secrecy-property-in-cryptography-attribute-based-encryption
https://en.wikipedia.org/wiki/Forward_secrecy
https://sunhuachuang.gitbooks.io/sun-note/content/cryptography/forward_backward_secrecy.html
https://users.ece.cmu.edu/~adrian/projects/sec/node6.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号