单像素成像中观测矩阵的设计

1.2022-Deep Learning Optimized Terahertz Single-Pixel Imaging
创新点：However, all these reports focus on reducing the sampling rate or the number of patterns M, but leave the sampling time per pattern t0 untouched.
观测矩阵：However, these compressed sensing algorithms adopt nonorthogonal random patterns, hindering further compression of the sampling ratio. To tackle this problem, deterministic model-based techniques, which adopt deterministic orthogonal basis patterns such as Hadamard patterns or Fourier patterns to encode the THz fields, and utilize matrix operations to reconstruct THz images, have been proposed recently.
重建算法：Most ghost imagingmodels based on deep convolutional neural networks do not make full use of the hierarchical features from the original low-quality images, thereby resulting in relatively-low performance.

2.2020-Broadband high-resolution terahertz single-pixel imaging(调制器调制深度100%)
观测矩阵：There are many methods to generate patterns for masking an object (with ON and OFF pixels that transmit and block the optical signal, respectively), including the Hadamard, Fourier , and Toeplitz methods. The generated masks should be orthogonal to each other and equally ON:OFF pixel weighted for faster reconstruction. However, pseudo-random pattern reconstruction methods, i.e., nonorthogonal patterns with a small number of new pixels per mask, have been proven to be as effective as those using fully random patterns. 

3.2023-High-efficiency terahertz single-pixel imaging based on a physics-enhanced network
观测矩阵：CS-based terahertz single-pixel imaging still suffers from relatively long acquisition and reconstruction time due to the large number of measurements, especially for large-sized images. To tackle this problem, deterministic model-based techniques, which adopt deterministic orthogonal basis patterns such as Hadamard patterns or Fourier patterns to encode the terahertz beams, and utilize matrix operations to reconstruct terahertz images, were developed recently in the optical band.
However, at undersampling conditions, deterministic model-based techniques truncate the spectrum by acquiring the low-frequency part and discarding the high-frequency part, resulting in undesirable artifacts such as ringing artifacts in the reconstructed images.

4.2019-Terahertz wave near-field compressive imaging with a spatial resolution of over λ/100
观测矩阵：The Hadamard matrix with the best noise suppression performance among various measurement matriceswas used in our experiment.
重建算法：To save acquisition time, we compressed the obtained THz images by post-processing subsampled data. Given some assumptions about the sparsity ofthe imaging target, compressive sensing (CS) guarantees the fidelity of the compressed image with fewer measurements (M≪ N). Min-TV, one of several well-developed CS algorithms, behaves best for the compressive imaging ofan object with low curvature.

5.2018-Mask Responses for Single-Pixel Terahertz Imaging
Since the mask properties are of such importance for the image quality and all published work in this area has so far not focused on different mask types in an unintentional compressive case. Only Bernoulli and Hadamard masks are able to produce a reasonably good image of the single metallic edge. The Gaussian masks produce a THz representation of the edge that shows already significant distortions in the case where the number of measurements is equal to the number of pixels(100%). As can also be seen in Fig.2 only the Bernoulli masks show good compression results of the metallic edge even when only random 50% of the measured values are used for reconstruction. According to this analysis, only the pseudo-random Bernoulli masks exhibit potential for compressive imaging. 

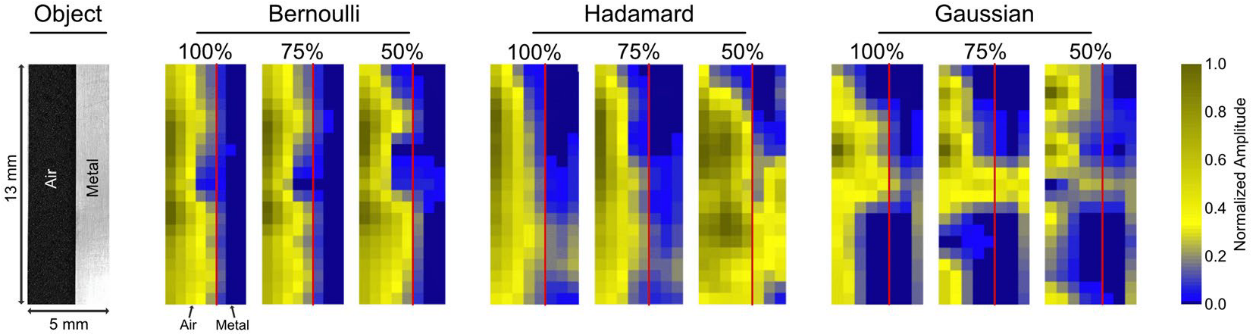
The Hadamard mask measurements provide a large modulation for specific masks but in a compressive imaging modality, where a random part of the measurements is not considered for reconstruction, their application was found to be not optimal. As shown by the investigation presented here only pseudo-random mask type measurements give sufficient compressibility in the pixel domain. The compressibility of pseudo-random masks coincides with a robustness property against transmission/measurement error.
As stated before, the robustness and compressibility properties of pseudo-random masks (Bernoulli masks) are very beneficial for the imaging process. Still, the reconstruction approaches are still lacking reconstruction speed. When real-time reconstruction speed is necessary Hadamard masks are still a good choice.

6.2017-Compressed sensing with near-field THz radiation
Further, it is known that an orthogonal basis minimizes the detector noise.
Adaptive sampling and compressive sensing are both strategies that make use of assumptions about the nature of the object (such as object sparsity when represented in a particular basis) to choose one solution that most likely represents the object. Using adaptive sampling, we first measure a low-resolution image and then sample regions of interest with progressively higher resolution. In short, identification of coarse edges from this initial low-resolution image determines where to sample with higher resolution, thus reducing the total number of measurements that are made. Edge identification is achieved via a single-tier 2DHaar wavelet decomposition of the low-resolution image. The Haar wavelet transform is a hierarchical structure that highlights the presence of edges at progressively finer scales: edge features yield large wavelet coefficients, while more uniform areas yield low wavelet coefficients. In our experiment, after each higher resolution resampling phase, edge detection is performed on the new image, and the process is repeated until the required resolution is reached. Compressed sensing is an alternative non-adaptive approach that makes assumptions about the object to reduce total number of measurements. This can include knowledge of the basis in which the representation of the image is sparse, or the basis in which the total variance or curvature of the object is expected to be low. Such assumptions typically hold for a wide variety of images, and compressed sensing theory shows how to then recover an image using fewer measurements than the number of pixels in the image. 
In this work we make the assumption that the total curvature of the image will be low. We sample the object using a set of random binary patterns, which are chosen due to their high degree of incoherence with respect to a wide range of sparse basis representations. Non-adaptive compressed sensing has the advantage that masks can be designed (and loaded onto a modulator) ahead of time rather than in response to measurement, as is the case for adaptive sampling.
Note that, in both our sampling strategies, we have applied regularization to combat noise in our measurements. This essentially allows the reconstruction algorithm to permit solutions that deviate from the measurements by an amount based on the estimated noise level, while seeking to minimize the level of curvature in the reconstruction.
The next tier of imaging is performed by making a series of Hadamard projection measurements using a fully sampled set of patterns confined to the regions defined by the mask. Here the commonly used Sylvester Hadamard construction is no longer optimal, as the number of patterns (and therefore pixels) in the Sylvester Hadamard sets are confined to 2^k, where k is a nonnegative integer, while the number of pixels within the next phase is unlikely to equal 2^k. Therefore we now use the Paley type-I Hadamard construction, which is of more flexible scale, since it can possess a number of patterns equal to p + 1, where p is a Prime number that is congruent to 3 (mod 4). Therefore we create the smallest Paley type-I Hadamard matrix which can be used to critically or slightly oversample the target area of the object defined by the mask, at twice the resolution of the initial low resolution initial image I1. The fully sampled higher resolution image of the masked regions is once again reconstructed from a weighted sum of the Paley Type-I Hadamard patterns, each weighted by its measured correlation with the object.