平面 题解

平面
【问题描述】
二维的空间即是平面。我们在二维空间中定义直角坐标系，并用网格将空间划分为单位面积的一块一块，并给每块一个二维坐标。我们假设有一个小生命生活在二维空间中从(1,1)到(n,m)的共n×m块的矩形区域中，二维生命体一开始可以处于任意一块中，并且可以移动到上下左右相邻的一块中，但是不能越过矩形的边界。现在有一个高维的生命体闯入了这个世界，并开始制造混乱。高维生命体改变了格子的高度，使得没有任意两个相邻格子的高度相同。这样空间就变成了三维空间。但对于二维生命体来说，整个空间还是一个平面，只是它无法从一个高度较低的格子移动到相邻的高度较高的格子。二维生命体可以从任意一个格子开始移动，并在除起点外的任意一个可到达的格子处停下。一条移动的路径定义为沿途经过的所有格子的序列，路径长度为经过的格子数减1。不难发现，路径的条数是有限的。现在告诉你每一块格子的高度，你能求出所有可能路径的长度的0~k次方的和吗？由于答案可能很大，你只需要输出每个答案对12345取模后的结果。
【输入格式】
输入文件的第一行包含三个正整数n、m和k。
接下来的n行每行包含m个绝对值不超过10^9的整数，分别表示每个格子的高度。
【输出格式】
输出k+1行，每行包含一个整数。第i行的整数表示所有可能路径的长度的i−1次方之和对12345取模后的值。
【样例输入】
3 4 3
1 2 3 4
4 3 2 1
1 2 3 4
【样例输出】
38
66
136
318

 

DP，将格子排序，f[i]表示从i出发的路径数，g[i]为路径总长。f[i]=Σf[j]，g[i]=Σ(f[j]+g[j])，j为与i相邻的编号。

s[k][i]为从i出发的路径的k次方和，设到j的长度为aj[1...p]，s[k][j]=Σx(aj[x])^k，s[k][i]=ΣjΣx(aj[x]+1)^k。

转移：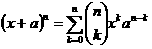

 令a=1，

复杂度：O(nm log nm +nmk²)

 

附代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <string>
#include <iomanip>
#include <ctime>
#include <climits>
#include <cctype>
#include <algorithm>
#define clr(x) memset(x,0,sizeof(x))
#define LL long long
#ifdef WIN32
#define AUTO "%I64d"
#else
#define AUTO "%lld"
#endif

using namespace std;

const int N = 300;
const int K = 50;
const int mod = 12345;
const int V[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};

class point {
    public:
    int x, y, h;
    point() { }
    point(int _x, int _y, int _h) : x(_x), y(_y), h(_h) { }
    bool operator < (const point &p) const { return h < p.h; }
} p[N*N+1];

int n,m,k,a[N+1][N+1],ans[N+1],C[K+1][K+1],d[N*N+1][K+1];

inline int node(int x, int y) { return (x-1)*m+y; }

int main() {
    freopen("plane.in","r",stdin);
    freopen("plane.out","w",stdout);
    scanf("%d%d%d",&n,&m,&k);
    C[0][0] = 1;
    for(int i = 1; i <= k; ++i) {
        C[i][0] = C[i][i] = 1;
        for(int j = 1; j < i; ++j) {
            C[i][j] = C[i-1][j-1]+C[i-1][j];
            if(C[i][j] >= mod) C[i][j] -= mod;
        }
    }
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j) {
            scanf("%d", &a[i][j]);
            p[node(i, j)] = point(i, j, a[i][j]);
        }
    sort(p+1, p+n*m+1);
    for(int i = 1; i <= n * m; ++i) {
        int r = node(p[i].x, p[i].y);
        d[r][0] = 1;
        for(int v = 0; v < 4; ++v) {
            int x = p[i].x+V[v][0], y = p[i].y+V[v][1];
            int q = node(x, y);
            if(x < 1 || x > n || y < 1 || y > m || a[x][y] >= p[i].h) continue;
            d[r][0] += d[q][0];
            if(d[r][0] >= mod) d[r][0] -= mod;
            for(int j = 1; j <= k; ++j)
                for(int l = 0; l <= k; ++l) {
                    d[r][j] += (C[j][l]*d[q][l])%mod;
                    if(d[r][j] >= mod) d[r][j] -= mod;
                }
        }
        for(int j = 0; j <= k; ++j) {
            ans[j] += d[r][j];
            if(ans[j] >= mod) ans[j] -= mod;
        }
    }
    ans[0] -= (n * m) % mod;
    if(ans[0] < 0) ans[0] += mod;
    for(int i = 0; i <= k; ++i) printf("%d\n", ans[i]);
    return 0;
}