Soft Renderer的乐趣
最近这一个月的闲暇时间在边学习《3D编程大师技巧》边做自己的Soft Renderer,一个月下来总算有了个“基本原型”的样子。主要是在编写图形管线的过程式代码,简单明了为第一个阶段的目标。
今天加入了“透视校正纹理映射”这个必不可少的图形基本特性,计算公式抠自《Real-Time Rendering》2th的第十五章“透视校正插值”一节的引用文章Blinn大拿的《W Pleasure W Fun》。即对UV纹理坐标进行所谓的双曲线插值。。。用起来倒是很简单,大致意思就是:
透视投影变换不是一个仿射变换,它会扭曲投影后的图形,使得原本在eye space呈线性的z值在投影空间不再线性,故而推出直接使用模型属性(UV,顶点颜色等)来进行投影空间的线性插值是错误的。而投影空间z值根据推导对于1/z是线性的,所以只要根据u/z,v/z进行插值就正确了,这就是透视校正纹理映射。
我思考了下,我们在投影变换后的齐次除法这一步,将顶点坐标x,y,z除以w,就能将顶点从投影空间变换到[-1,1]的CVV空间,最终的UDC坐标是线性的。而根据OpenGL透视投影矩阵:
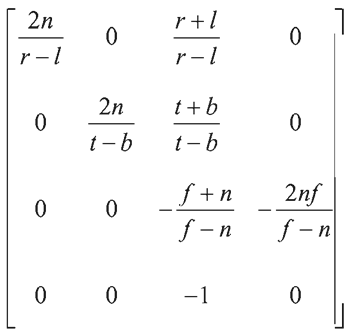
可知,点(x,y,z,1)经变换后为(x1,y1,z1,-z),即w=-z,所以齐次除法似乎也是利用了关于1/z线性这个公式。这完全是我的瞎推测,不对请高手指出。。。
总结起来就是,透视投影变换不是一个仿射变换,而是让变换后的点关于1/z呈线性的变换。
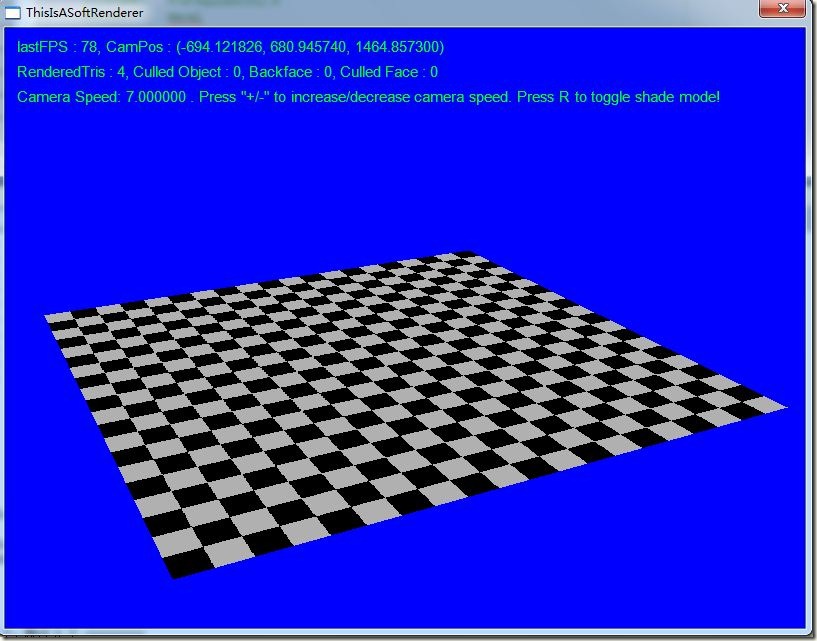
下面是未进行透视校正和进行了校正的两张对比图:
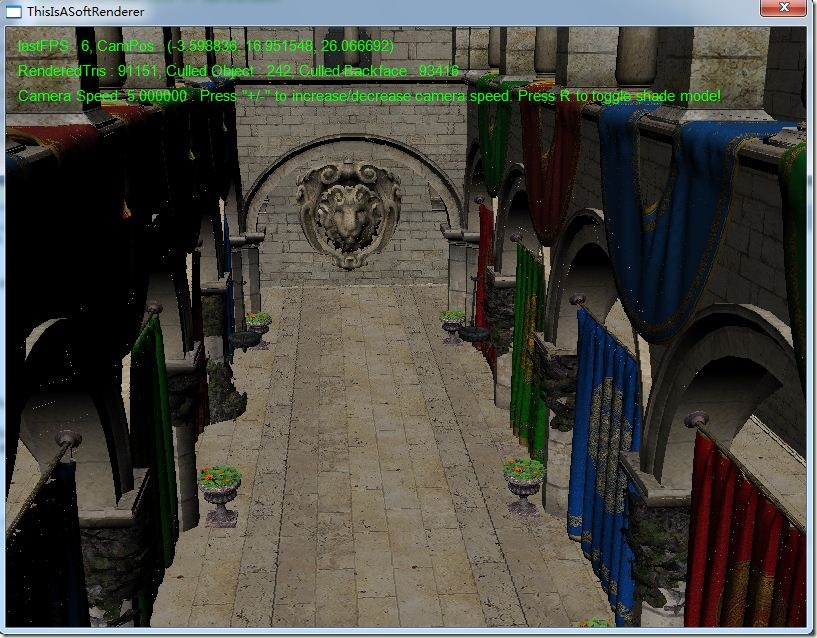
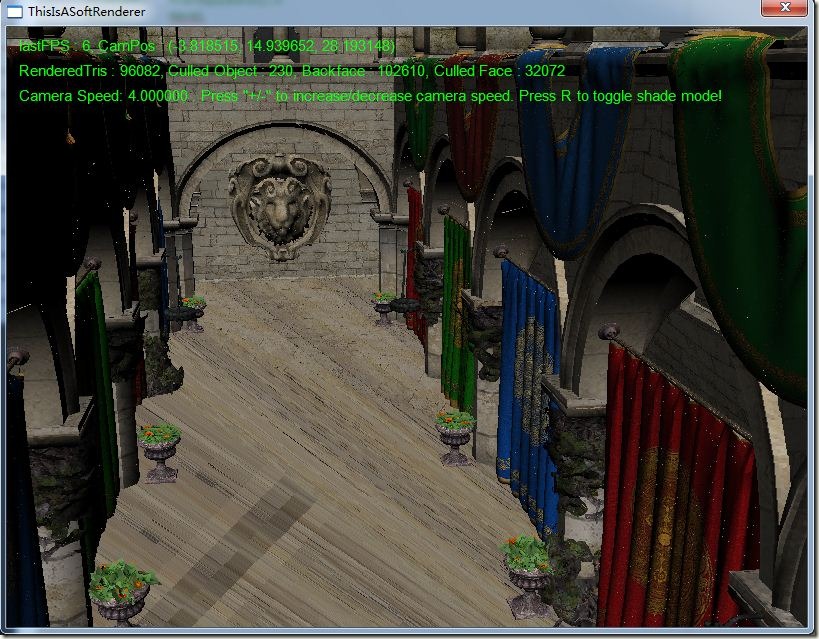
Sponza场景的校正和未校正比较图:
只是使用Blinn大神在1998年给出的这个计算公式的话,是很简单的,几句代码的事。厘清整个理论的数学推导就不那么容易了。。。这也是Blinn大拿之所以称为大师的原因。详细数学推导我这里上传一份文档,是大师的《Jim Blinn’s Corner:Notation,Notation,Notation》,在第十章《W Pleasure W Fun》中。没什么花哨的,跟往常一样。。。大拿行云流水的玩弄着数学公式,展示着数学图表,我这个数学彩笔一如既往的痛不欲生。不过感觉还是比以前好些了,我弄明白了很多基本问题,如什么是线性z,透视投影变换的更多细节等。不要浮躁,我们需要的是端正的在键盘旁摆上一个艹搞本。。用直尺和铅笔模仿大师的思路进行推导。。
对于Blinn爷爷,高爷爷这样的老学究,感觉一个气质啊,霸气,随性。出书都是无比霸气的封面。。。。。如下(绝对没有黑的意思!):
做Soft Renderer很有趣很有收获,我觉得这是图形程序员都应该锻炼的一关。我这里收集了一些可供参考的大牛前辈(大家通常都活跃于OpenGPU论坛)的软渲作品,真的是各有千秋啊,也让我有了前进的动力。
1.鬼火(Irrlicht)引擎的SoftRenderer和BurningVideo软渲染器.前者是作者自己写的,比较不完善,后者是爱好者加入的,更完善,所以称为"on steroids(打了鸡血的渲染器)"...
2.空明大的软渲染器salviar.
http://www.cppblog.com/lingjingqiu/archive/2009/12/07/102698.html
3.乔捷大的Hybrid3D软渲染器,可惜好像没开源,不能学习精华.
http://www.cnblogs.com/Hybird3D/archive/2013/02/11/Rasterization_in_Hybird3D.html
4.易恺铭大的软渲染器.
http://sr.codeplex.com/
5.姚勇大的软渲染器.
http://www.cnblogs.com/puzzy3d/archive/2008/07/25/1251656.html
5.<<Real-Time Rendering>> + <<3D编程大师技巧>>. 理论与实践的完美结合。。
update:
2013-8-7 :目前已完成Phong逐像素光照模型,光栅化实在已经感觉吃不消了,帧数从Gouraund的10几帧降到了1帧,果然是CPU计算密集型应用啊。。那 些还加入了法线贴图,SSAO等高级效果的软渲,本屌真心给跪了!。。。。现在开始进入第二阶段:性能优化乃至管线优化,重点思考怎么利用多核多线程甚至 SIMD来并行计算,来解决光栅化部分的过高瓶颈问题。
2013-8-19:加入多线程支持(线程池,生产者-消费者模型)。不过貌似加速比为1啊。。。嗯,看来我的多线程有问题。
2013-11-9:加入了法线贴图,效果一下子让我眼前一亮,果然要有法线贴图人生才完整呢。。。。。
终于完全理解了切空间的几何意义:
p = ux * T + uy * B
一言以蔽之,这个等式的几何意义就是把该点的UV(位于texture sapce)在object space线性表示出来~
推广到坐标系,故而TB就是texture space坐标基(1,0)(0,1)在object space的表示,故而MatrixTBN是从texture space变换到object space。
以前总在疑惑,这个切空间为什么可以把uv和position强扯上关系呢,现在明白了,这个地方我们不要用局部的视角(即某点的uv,position)来看待,而要用整体的视角(texture space, object space),这也是矩阵的整体-局部思想的一个体现吧。
切空间的完善计算流程也是值得学习的,鬼火的做法貌似过时了。。。OGRE倒是与时俱进,参考下面两篇文章:
http://www.terathon.com/code/tangent.html
http://www.sssa2000.com/?p=686
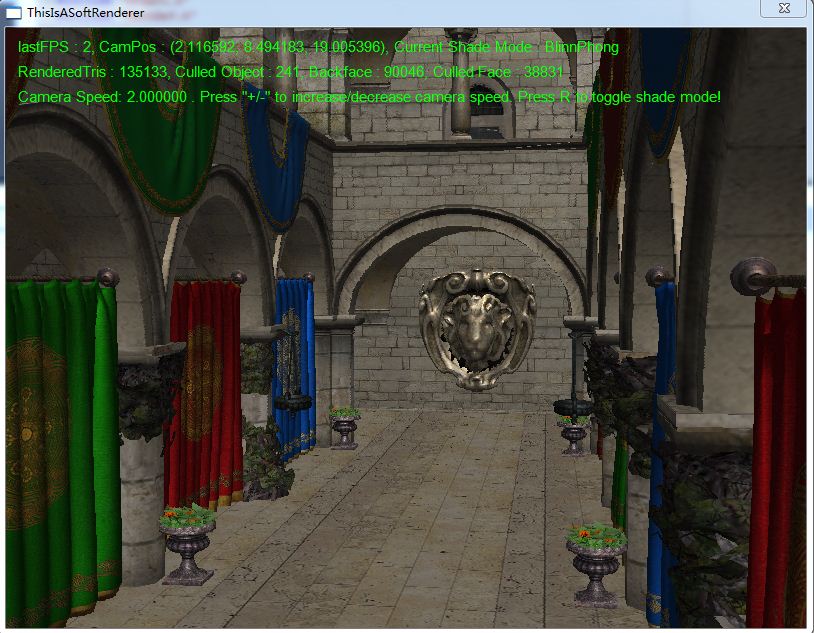
没有法线贴图
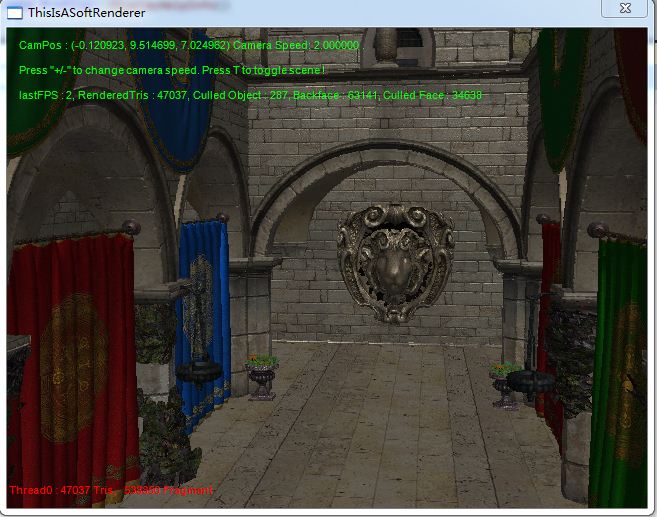
开启法线贴图






 浙公网安备 33010602011771号
浙公网安备 33010602011771号