《机器学习》第一次作业——第一至三章学习记录和心得
第一章 模式识别基本概念
模式识别基本概念
模式识别的定义:根据已有知识的表达或者说是函数映射,针对待识别模式,判别决策其所属的类别或者预测其对应的回归值,是一种推理过程,可划分为“分类”和“回归”两种形式。
模式识别数学表达
输入空间和输出空间:原始输入数据x所在的空间,输出的类别/回归值y所在的空间
分类:输出量是离散的类别表达,即输出待识别模式所属的类别——二类/多类分类
回归:
- 输出量是连续的信号表达(回归值)
- 输出量维度:单个或多个维度。
- 回归是分类的基础:离散的类别值是由回归值做判定决策得到的。
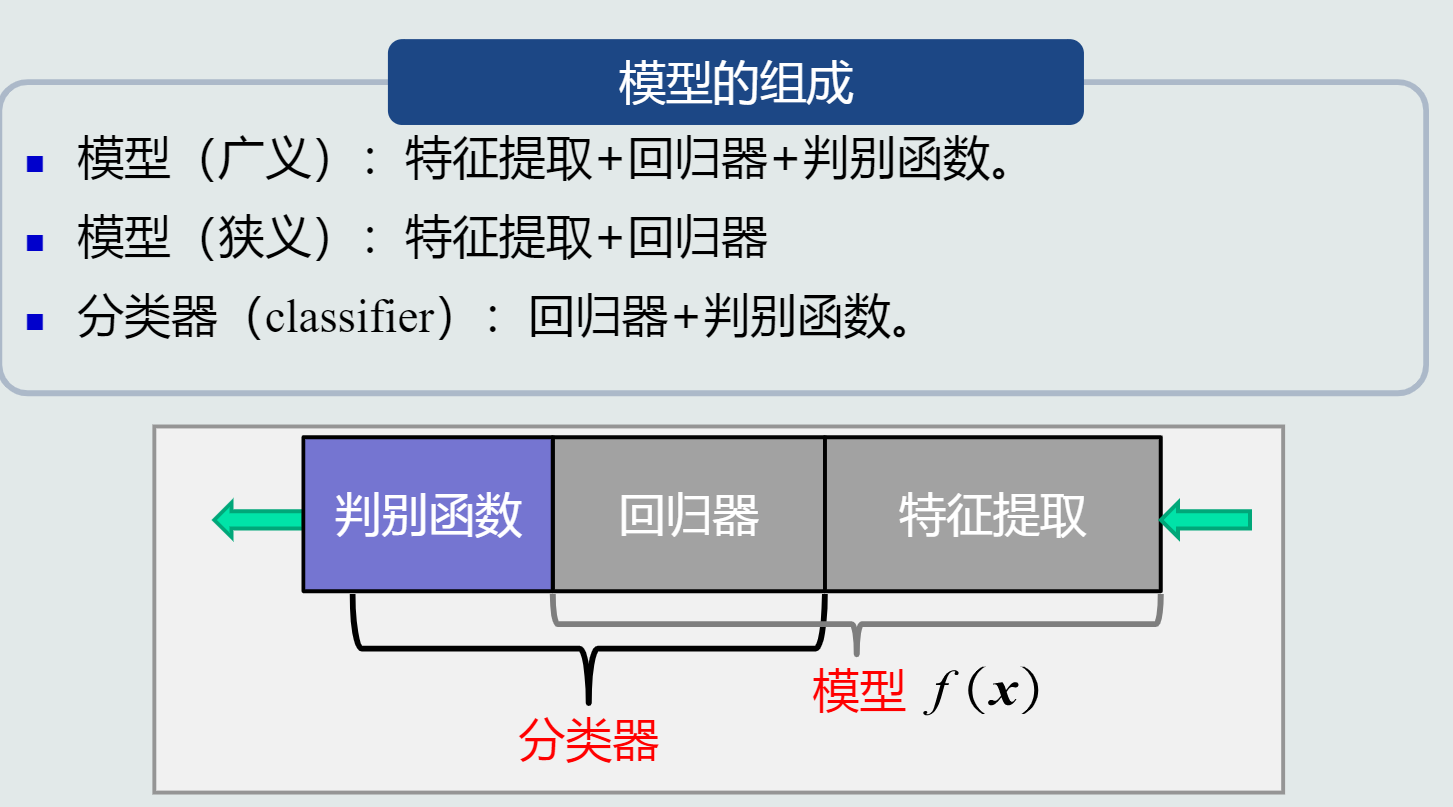
模型:关于已有知识的一种表达方式,即函数f(x)。模型可用于回归和分类。
判别函数:判别函数使用一些特定的非线性函数来实现,通常记为函数g,通常判别函数固定,所以不把它归于模型的一部分。判别器中,sign函数用来进行二类分类(判断回归值>0还是<0),max函数用来进行多类分类(取最大的回归值所在维度对应的类别)。
特征向量:

特征向量的相关性
- 点积具备对称性,向量投影不具备对称性。
- 残差向量指向量x分解到向量y方向上得到的投影向量与原向量x的误差。
- 特征向量之间的欧氏距离可以表征两个向量之间的相似程度。
机器学习基本概念
线性模型:模型结构是线性的(直线、面、超平面):y=(W^T)x+W0(w,w0是模型参数)
非线性模型:模型结构非线性,y=g(x)。常见非线性模型:多项式、神经网络、决策树
样本量与模型参数量的关系:N=M:参数有唯一解;N>>M:没有准确的解;N<<M:无数个解/无解
目标函数:对于over-determined的情况,需要额外添加一个标准,通过优化该标准来确定一个近似解,这个标准就是目标函数,也叫代价函数或损失函数
机器学习方式:真值(标签)&标注;监督式学习:训练样本及输出真值都给定情况下的机器学习;无监督式学习:只给定训练样本,没有给输出真值情况下的机器学习算法;半监督式学习:既有标注的训练样本,又有未标注的训练样本情况下的学习算法
强化学习:机器自行探索决策、真值滞后反馈的过程
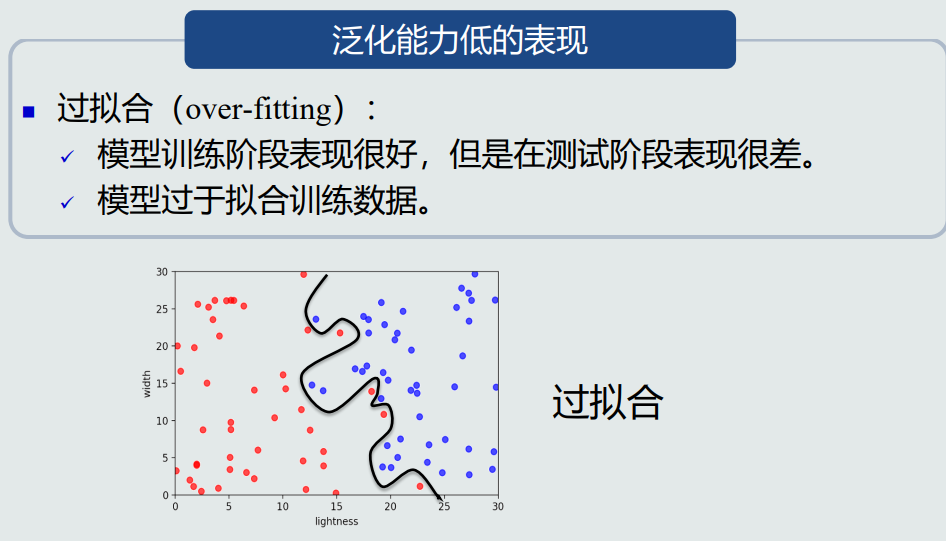
模型的泛化能力
- 泛化能力:学习算法对新模式的决策能力。
- 训练集是模型训练所用的样本数据,集合中的每个样本称作训练样本;测试集是测试模型性能所用的样本数据,集合中的每个样本称作测试样本。
- 测试样本假设从样本真实分布中独立同分布(iid)。
- 测试误差也称泛化误差。
- 过拟合是泛化能力低的表现。
评估方法与性能指标
评估方法:
- 留出法:随机划分:训练集和测试集,用训练集训练模型,用测试集评估模型量化指标;取统计值:取量化指标的平均值/方差/最大值等作为最终性能量化评估结果
- K折交叉验证:将数据集分割成K个子集,从中选取单个子集作为测试集,其余作为训练集;交叉验证重复K次,使每个子集被测试一次;K次评估值取平均作为最终量化评估结果
- 留一验证:每次只取数据集中一个样本做测试集,其余做训练集;每次样本测一次,取所有评估值的平均值作为最终评估结果;等同于K折交叉验证,K为数据集样本总数
准确度=(TP+TN)/(TP+TN+FP+FN)。
精度=TP/(TP+FP)。
召回率=TP/(TP+FN)。
F-score=((a2+1)精度召回率)/(a2*精度+召回率),a为常数。
PR曲线:横轴召回率,纵轴精度。
ROC曲线:横轴为1-specificity,纵轴为召回率。
AUC:曲线下方面积。
基于距离的分类器
MED分类器
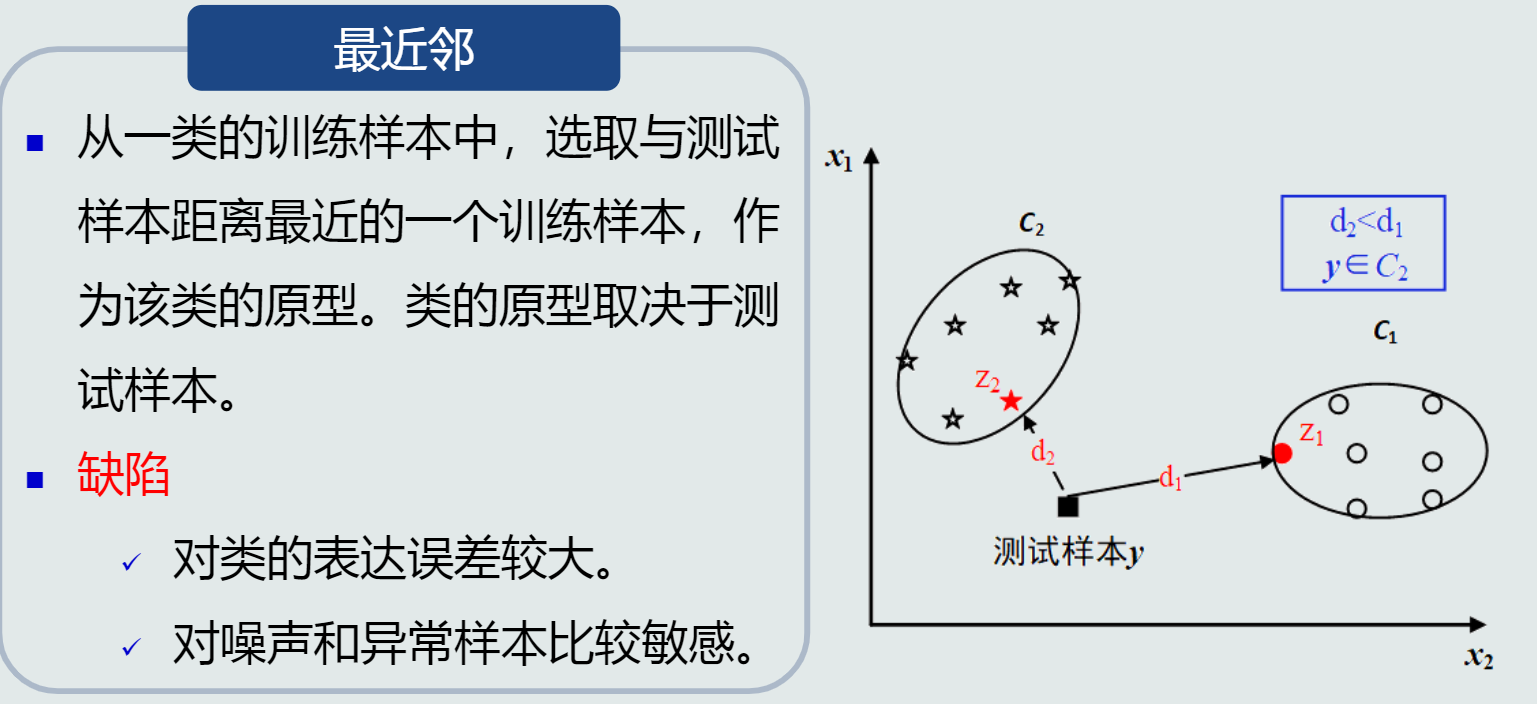
- 几种“距离”:欧氏距离、曼哈顿距离(绝对值距离、出租车几何)、切比雪夫距离(国际象棋中国王可以移动的位置)、闵式距离、马氏距离等。
- MED分类器:最小欧式距离分类器。
- MED分类器在高维空间中的决策边界是一个超平面。
同一性:d(x,z) = 0,iff x = z
非负性:d(x,z) >= 0
对称性:d(x,z) = d(z,x)
三角不等式:d(x,z) <= d(x,y) + d(y,z)
特征白化
- 目的:将原始特征映射到一个新的特征空间,使得在新空间中特征的协方差矩阵为单位矩阵,从而去除特征变化的不同及特征之间的相关性
- 步骤:1.去除特征之间的相关性——解耦:通过W1实现协方差矩阵对角化;2.对特征进行尺度变换——白化:通过W2对上一步变化后的特征再进行尺度变换,实现所有特征具有相同方差。
MICD分类器
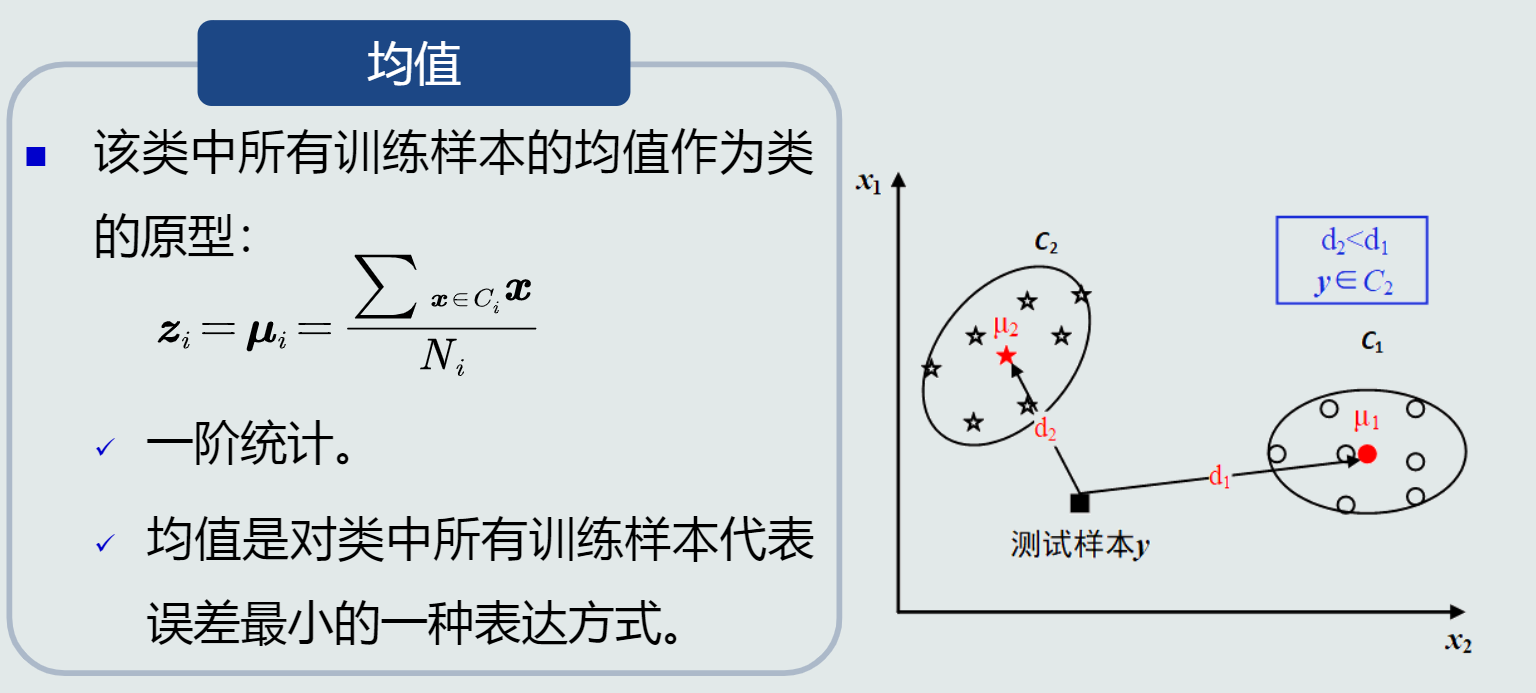
概念:最小类内距离分类器,基于马氏距离的分类器
- 距离度量:马氏距离
- 类的原型:均值
第三章 贝叶斯决策与学习
贝叶斯决策与MAP分类器
后延概率:给定一个测试模式x,决策其属于哪个类别需要依赖于P(Ci|x),该表达式称为后验概率,表达给定模式x属于类Ci的可能性。
贝叶斯规则:要获得后延概率,就要利用贝叶斯规则

map分类器:将测试样本决策分类给后验概率最大的那个类。给定所有测试样本, MAP分类器选择后验概率最大的类,等于最小化平均概率误差,即最小化决策误差。
MAP分类器:高斯观测概率
- 先验和观测概率表达方式:1.常数表达:P(Ci)= 0.2;2.参数化解析表达:高斯分布……;3.非参数化表达:直方图、核密度、蒙特卡洛……
- MAP分类器会倾向于选择先验概率大,分布紧致的类,解决了MED和MICD的问题

决策风险与贝叶斯分类器
决策风险:不同的错误决策产生完全不一样的风险。
损失:表征当前决策动作相对于其他候选类别的风险程度
决策风险的评估:给定一个测试样本x,分类器决策其属于Ci类的动作对于的决策风险可以定义为相对于所有候选类别的期望损失。
贝叶斯分类器:在MAP分类器基础上,加入决策风险因素,得到贝叶斯分类器。贝叶斯分类器选择决策风险最小的类,即最小化期望损失。
朴素贝叶斯分类器:当特征是多维的,假设特征之间是相互独立的,从而得到以下公式
拒绝选项:当测试数据在决策边界时,即使选择后验概率高的,该概率的值仍然可能很小。为了避免错误决策,引入阈值,当概率低于阈值时不决策
最大似然估计
参数化方法:给定概率分布的解析表达,学习这些解析表达中的参数,又称参数估计
最大似然估计:

最大似然的估计偏差
- 无偏估计:如果一个参数的估计量的数学期望是该参数的真值,则该估计量称作无偏估计,意味着只要训练样本个数足够多,该估计值就是参数的真实值
- 高斯分布均值的最大似然估计是无偏估计;高斯分布协方差的最大似然估计是有偏估计
贝叶斯估计
- 贝叶斯估计:给定参数𝜃分布的先验概率以及训练样本,估计参数θ分布的后验概率
- 贝叶斯估计具备不断学习的能力。允许最初不太准确的估计,随着训练样本的不断增加而修正估计值,从而达到期望真值
- 贝叶斯估计流程步骤

- 贝叶斯估计与最大似然估计的对比:贝叶斯估计把参数看作参数空间的一个概率分布,依照训练样本来估计参数的后验概率,从而得到观测似然关于参数的边缘概率,随着样本个数逐渐增大,贝叶斯估计越来越能代表真实的观测似然分布。最大似然估计的参数是确定值,不需要估算参数的边缘概率。
KNN估计

直方图与核密度估计
KNN估计的问题:在推理测试阶段仍需存储所有训练样本。对任意模式x,需要以其为中心,在训练样本中选k个相邻点估计该模式的概率;区域R是由第k个相邻点确定的,易受噪声影响
直方图估计:直接将特征空间划分为m个格子(bins),每个格子是一个区域R,位置固定、大小固定,相邻格子不重叠,k值不需要给定
核密度估计:以𝒙为中心固定带宽h,计算落入R的样本个数,以此计算𝑝(𝒙)。
核密度估计的优缺点:可以自适应确定R的代销,克服了KNN估计存在的噪声影响。但是要储存所有训练样本,耗费空间大。
带宽选取的原则:泛化能力。因为给定训练样本数量是有限的,故要求根据训练样本估计出的概率分布既能符合训练样本,同时也要有一定预测能力,即能估计未看见的模式


