OFDM系统PAPR算法的MATLAB仿真,对比SLM,PTS以及CAF,对比不同傅里叶变换长度

1.算法运行效果图预览

(完整程序运行后无水印)

 

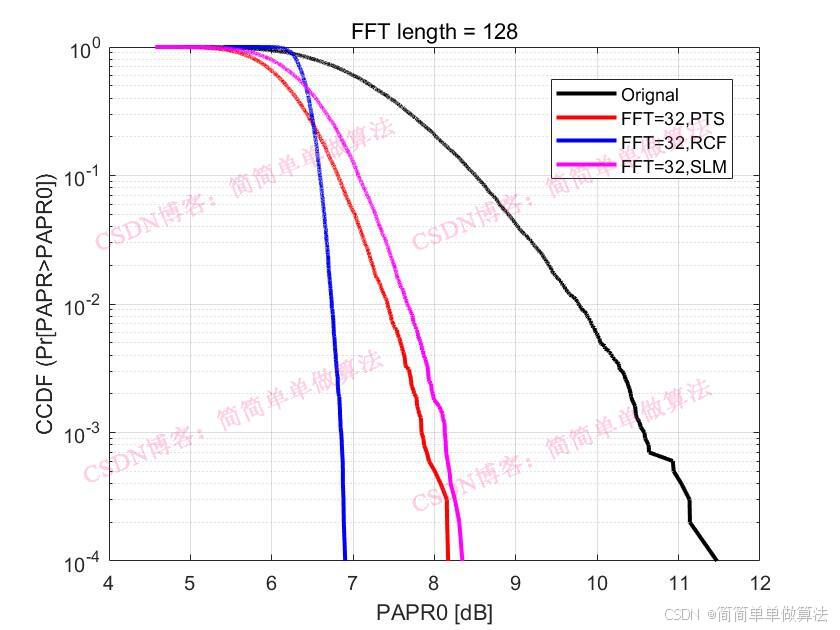
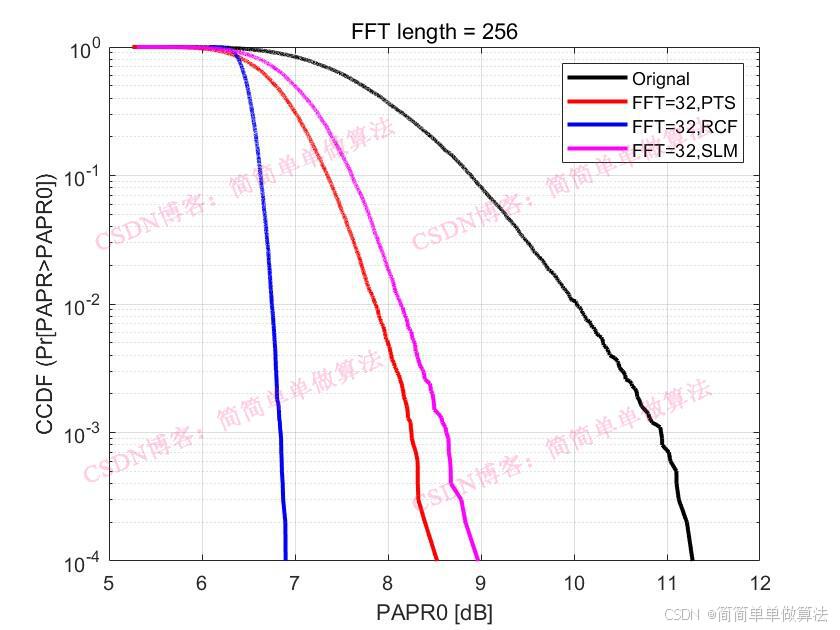
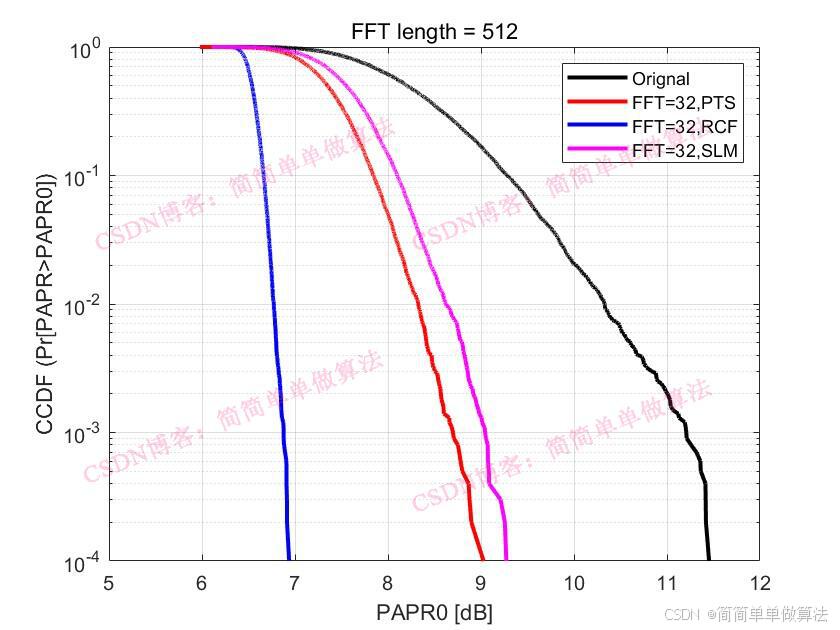
2.算法运行软件版本

matlab2022a

 

3.部分核心程序

（完整版代码包含详细中文注释和操作步骤视频）

for jj=1:Nbits
    Index(1,:)   = floor(length(MAP_qpsk)*rand(1,Lfft))+1; % 生成第一个符号的随机索引
    Index(2:N,:) = floor(length(Phases)*rand(N-1,Lfft))+1; % 生成其余符号的随机索引
    
    X(1,:)       = MAP_qpsk(Index(1,:)); % 原始频域信号
    Phase_Rot    = Phases(Index(2:N,:)); % 相位旋转
    X(2:N,:)     = repmat(X(1,:),N-1,1).*Phase_Rot; % 相位旋转后的频域信号
    
    x            = ifft(X,[],2); % 时域信号
    Pow1         = abs(x.^2); % 信号功率
    Pow2         = max(Pow1,[],2); % 峰值功率
    Pow3         = mean(Pow1,2);   % 平均功率
    
    PAPR_temp    = 10*log10(Pow2./Pow3); % 计算PAPR
    papr0(jj)    = PAPR_temp(1); % 存储原始PAPR
    papr_slm(1,jj)  = min(PAPR_temp(1:end)); % 存储SLM N=4的情况
end
 
% 计算累积分布函数
[cdf1, PAPR1] = ecdf(papr0); % 原始PAPR的CDF
[cdf2, PAPR2] = ecdf(papr_slm(1,:)); % SLM N=2的PAPR CDF
174

　　

4.算法理论概述

       在正交频分复用（Orthogonal Frequency Division Multiplexing, OFDM）系统中，高峰均功率比（Peak-to-Average Power Ratio, PAPR）是一个关键问题，因为它会导致功率放大器非线性失真、增加发射机功耗等问题。为了降低PAPR，研究人员提出了多种算法，其中包括选择映射（Selected Mapping, SLM）、相位截断星座图（Partial Transmit Sequences, PTS）等技术。

 

4.1、选择映射（SLM）

        选择映射（SLM）算法通过生成多个相位旋转的子载波数据，并选择具有最低PAPR的信号进行传输。假设原始信号为x，则生成N个相位旋转的信号xi​，其中 i=1,2,…,N。

 

 

 

4.2 相位截断星座图（PTS）

        PTS方法通过对部分子载波施加相位旋转来降低PAPR。假设将 K 个子载波分为 V 个组，每组内的子载波可以独立地施加相位旋转。