基于1bitDAC的MU-MIMO的非线性预编码算法matlab性能仿真
1.算法运行效果图预览
(完整程序运行后无水印)
2.算法运行软件版本
matlab2022a
3.部分核心程序
(完整版代码包含详细中文注释和操作步骤视频)
% 计算符号能量,归一化,以及其他参数
Energy = sqrt(mean(abs(Maps).^2));
Maps = Maps/Energy;
Lmaps = length(Maps);
bps = log2(Lmaps);
bits = de2bi(0:Lmaps-1,bps,'left-msb');
% 生成随机比特序列,映射到符号,添加噪声,构建信道矩阵等
Xbits = randi([0 1],Us,bps);
Ybits = bi2de(Xbits,'left-msb')+1;
Zmod = Maps(Ybits).';
Noise = (randn(Us,1)+1i*randn(Us,1))/sqrt(2);
H = (randn(Us,Ns)+1i*randn(Us,Ns))/sqrt(2);
H1 = sqrt(1 - Herr)*H + sqrt(Herr)*(randn(Us,Ns)+1i*randn(Us,Ns));
% 遍历预编码器类型
for j3=1:length(Pcd_sel)
% 遍历每个SNR值
for k=1:length(SNRs)
N0 = 10.^(-SNRs(k)/10);
if strcmp(Pcd_sel{j3},'ZF')==1
[x,beta] = func_zf(Zmod,H1);
end
if strcmp(Pcd_sel{j3},'WF')==1
[x, beta, ~] = func_WF(Zmod,H1,N0);
end
if strcmp(Pcd_sel{j3},'MRT')==1
[x, beta, ~] = func_MRT(Zmod,H1);
end
if strcmp(Pcd_sel{j3},'ADMM')==1
wb = 1;
[x, beta, vr] = func_ADMM(Zmod,H1,N0);
Vr_sets = [Vr_sets vr];
end
y = H*x + sqrt(N0)*Noise;
Y_ = beta*y;
[~,Iidx] = min(abs(Y_*ones(1,length(Maps))-ones(Us,1)*Maps).^2,[],2);
bhat = bits(Iidx,:);
err = (Ybits~=Iidx);
BER(m,j3,k) = BER(m,j3,k) + sum(sum(Xbits~=bhat))/(Us*bps);
end
end
end
154
4.算法理论概述
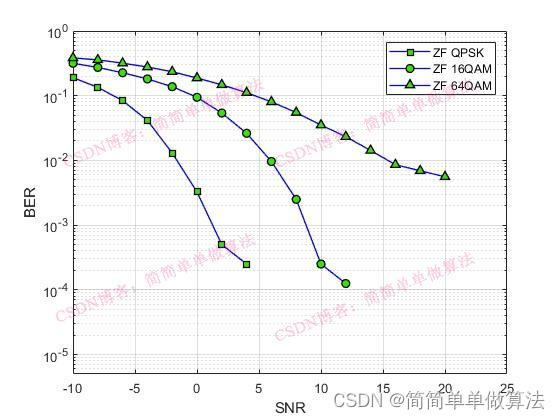
在现代无线通信系统中,多用户多输入多输出(MU-MIMO, Multi-User Multiple-Input Multiple-Output)技术是提高频谱效率和数据传输速率的关键。然而,高精度的数字模拟转换器(DAC)在大规模MIMO系统中成本高昂,能耗巨大,因此基于1-bit DAC的预编码技术应运而生,它通过仅使用1-bit的量化来显著降低硬件复杂度和功耗。本文将深入探讨基于1-bit DAC的MU-MIMO系统中的非线性预编码算法,并与传统线性预编码技术,如ZF(Zero-Forcing)、WF(Water-Filling)、MRT(Maximum Ratio Transmission)以及较为先进的ADMM(Alternating Direction Method of Multipliers)算法进行对比。
4.1 基于1-bit DAC的非线性预编码背景
在MU-MIMO系统中,预编码的目的是将多路信号映射到天线阵列上,以在接收端实现用户间的干扰消除或最小化。当使用1-bit DAC时,信号只能被量化为+1或-1,这导致预编码过程变得非常具有挑战性,因为它本质上是非线性的,需要设计特定的算法来逼近理想线性预编码的性能。
信号量化可表示为:

其中,sk是原始的复数预编码信号,s^k是量化后的信号,sign(⋅)sign(⋅)函数根据信号的实部和虚部确定量化结果。
一种常见的非线性预编码方法是基于符号最大化准则,即寻找一组预编码向量,最大化各个用户信号经过量化后的能量,同时考虑相互间的干扰。对于一个基站天线数为N,服务用户数为K的系统,接收信号模型可表示为:
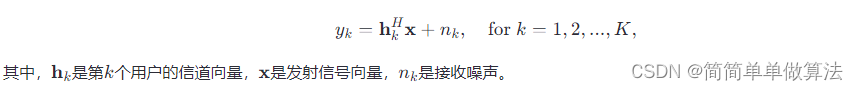
4.2 ZF(Zero-Forcing)
ZF预编码的目的是完全消除用户间的干扰,其预编码矩阵WZF满足:

其中,H是所有用户信道矩阵,H∗是H的共轭转置。
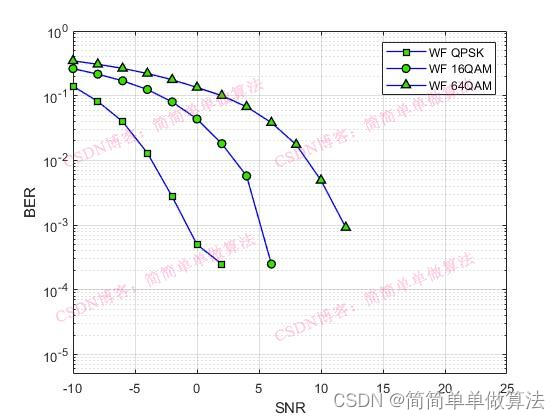
4.3 WF(Water-Filling)
WF算法是一种功率分配策略,用于优化每个子载波的发射功率,以最大化系统总吞吐量。其目标是解决如下优化问题:
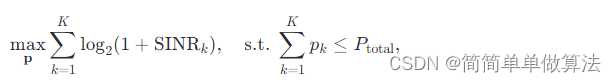
其中,p是功率分配向量,Ptotal是总功率预算,SINRk是第k个用户的信噪比。
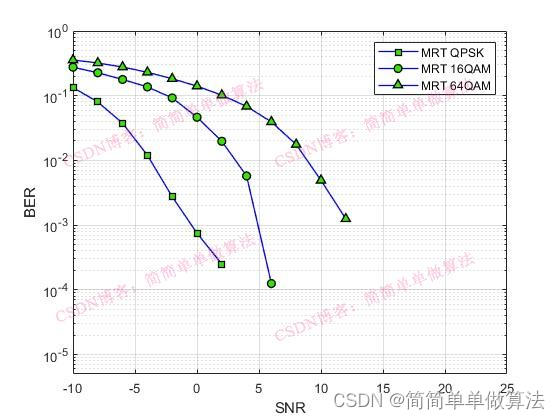
4.3 MRT(Maximum Ratio Transmission)
MRT预编码是基于信道增益的,目的是最大化信号能量与干扰加噪声比,其预编码向量为:

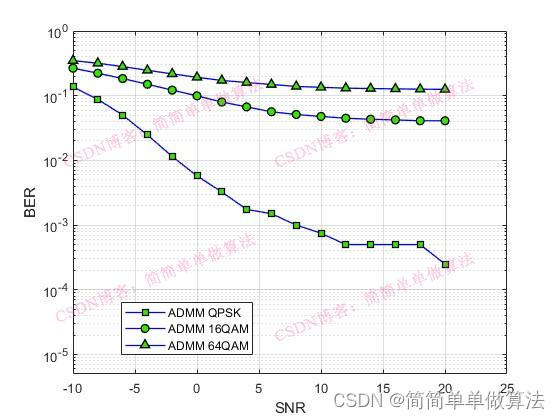
4.4ADMM(Alternating Direction Method of Multipliers)
ADMM是一种迭代优化算法,被用于解决带约束的优化问题,如在MU-MIMO系统中结合功率约束优化预编码矩阵。ADMM通过交替优化原始问题的不同子问题,达到全局最优解或近似最优解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号