基于PSO粒子群优化的CNN-LSTM的时间序列回归预测matlab仿真

1.算法运行效果图预览

 

 

2.算法运行软件版本

matlab2022a

 

3.部分核心程序

for i=1:Iter
    i
    for j=1:Npeop
        rng(i+j)
        if func_obj(x1(j,:))<pbest1(j)
           p1(j,:)   = x1(j,:);%变量
           pbest1(j) = func_obj(x1(j,:));
        end
        if pbest1(j)<gbest1
           g1     = p1(j,:);%变量
           gbest1 = pbest1(j);
        end
        
        v1(j,:) = 0.8*v1(j,:)+c1*rand*(p1(j,:)-x1(j,:))+c2*rand*(g1-x1(j,:));
        x1(j,:) = x1(j,:)+v1(j,:); 
         
        for k=1:dims
            if x1(j,k) >= tmps(2,k)
               x1(j,k) = tmps(2,k);
            end
            if x1(j,k) <= tmps(1,k)
               x1(j,k) = tmps(1,k);
            end
        end
 
        for k=1:dims
            if v1(j,k) >= tmps(2,k)/2
               v1(j,k) =  tmps(2,k)/2;
            end
            if v1(j,k) <= tmps(1,k)/2
               v1(j,k) =  tmps(1,k)/2;
            end
        end
 
    end
    gb1(i)=gbest1 
end
 
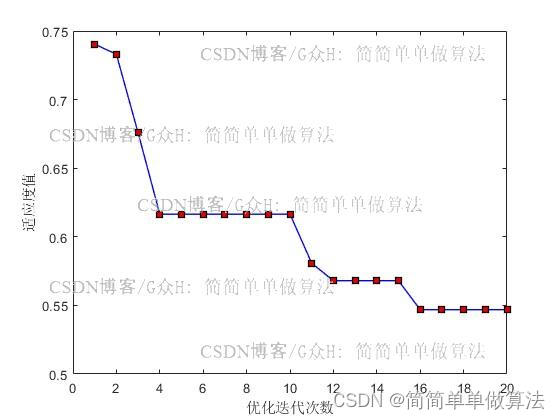
figure;
plot(gb1,'-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
 
xlabel('优化迭代次数');
ylabel('适应度值');
.....................................................
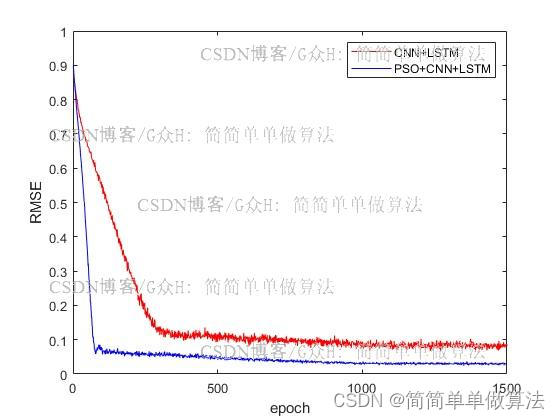
figure;
plot(IT(1:1:end),Accuracy(1:1:end));
xlabel('epoch');
ylabel('RMSE');
%数据预测
Dpre1 = predict(Net, Nsp_train2);
Dpre2 = predict(Net, Nsp_test2);
 
%归一化还原
T_sim1=Dpre1*Vmax2;
T_sim2=Dpre2*Vmax2;
 
 
%网络结构
analyzeNetwork(Net)
 
 
figure
subplot(211);
plot(1: Num1, Tat_train,'-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
plot(1: Num1, T_sim1,'g',...
    'LineWidth',2,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
 
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
grid on
 
subplot(212);
plot(1: Num1, Tat_train-T_sim1','-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
 
xlabel('预测样本')
ylabel('预测误差')
grid on
ylim([-50,50]);
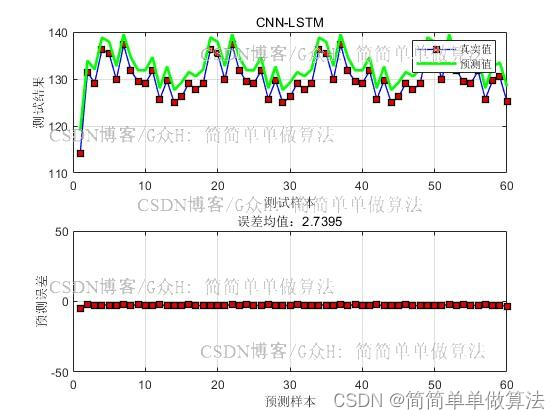
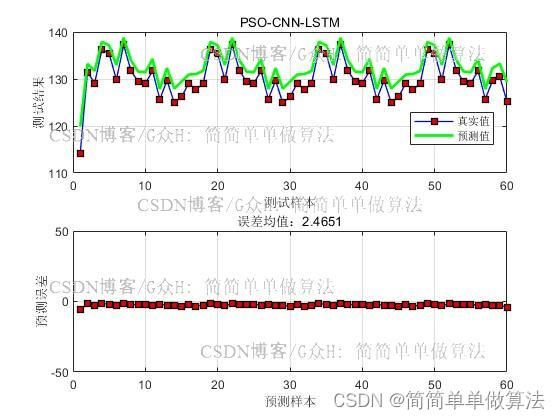
figure
subplot(211);
plot(1: Num2, Tat_test,'-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
plot(1: Num2, T_sim2,'g',...
    'LineWidth',2,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
legend('真实值', '预测值')
xlabel('测试样本')
ylabel('测试结果')
grid on
subplot(212);
plot(1: Num2, Tat_test-T_sim2','-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
 
xlabel('预测样本')
ylabel('预测误差')
grid on
ylim([-50,50]);
 
 
save R2.mat Num2 Tat_test T_sim2 gb1 Accuracy

　　

4.算法理论概述

        基于粒子群优化（Particle Swarm Optimization, PSO）的卷积神经网络-长短期记忆网络（Convolutional Neural Network - Long Short-Term Memory, CNN-LSTM）模型在时间序列回归预测中，结合了深度学习的强大表达能力和优化算法的高效搜索能力，为复杂时间序列数据的预测提供了一种强有力的解决方案。

 

4.1 卷积神经网络（CNN）

        CNN以其在图像识别领域的卓越表现而闻名，但其在时间序列分析中也显示出了强大的潜力。CNN通过局部连接和权值共享减少参数数量，利用卷积层捕获输入数据的空间特征。

 

 

 

4.2 长短期记忆网络（LSTM）

       LSTM是RNN的一种变体，特别擅长处理长序列依赖问题。它通过门控机制控制信息的遗忘、更新和输出，有效缓解了梯度消失/爆炸问题。

 

 

 

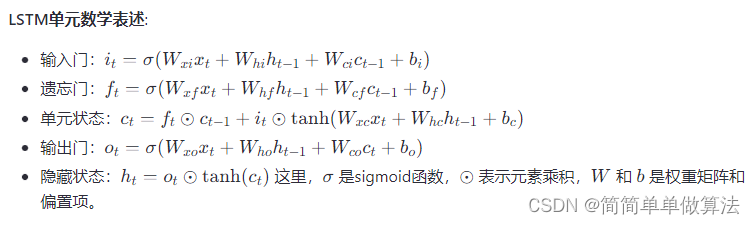
4.3 CNN-LSTM结合PSO的时间序列预测

       在时间序列预测任务中，首先使用CNN对输入序列进行特征提取，然后将提取到的特征作为LSTM的输入，进一步捕捉序列中的时序依赖关系。整个网络的参数（包括CNN的卷积核权重、LSTM的门控参数等）构成了PSO算法的搜索空间。

 

结合PSO的过程:

 

初始化一组粒子，每个粒子代表一组CNN-LSTM模型的参数。

对于每个粒子，构建相应的CNN-LSTM模型并训练，评估其在验证集上的预测性能（如均方误差MSE）作为适应度函数。

根据PSO算法更新粒子的位置和速度，不断寻找更优的模型参数配置。

迭代此过程直至满足停止条件（如达到最大迭代次数或找到足够好的解）。