基于FPGA的图像一维FFT变换IFFT逆变换verilog实现,包含tb测试文件和MATLAB辅助验证

1.算法运行效果图预览

fpga仿真结果

 

 

 

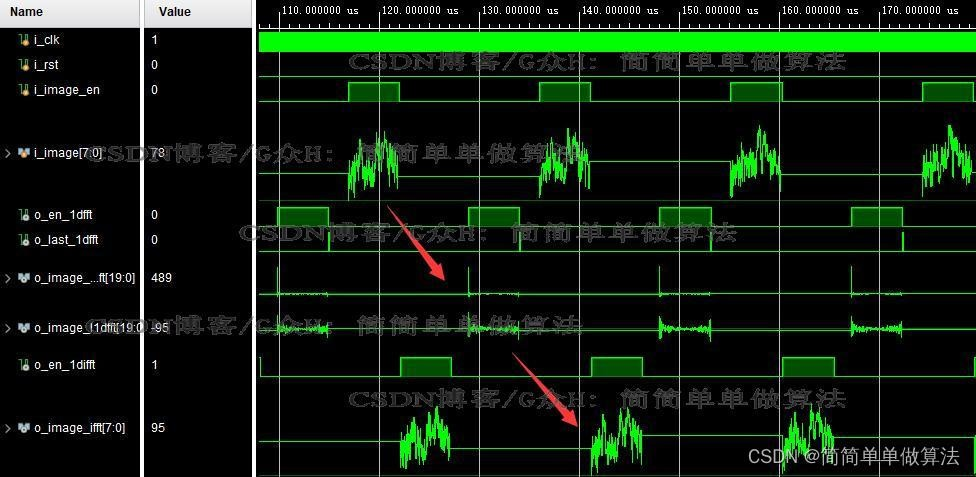
matlab调用FPGA的仿真结果进行图像显示

 

 

 

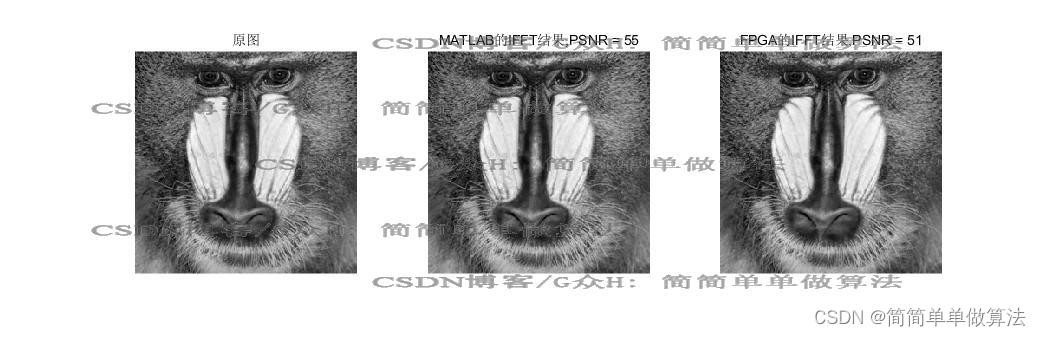
2.算法运行软件版本

vivado2019.2

 

matlab2022a

 

3.部分核心程序

 

 

module test_image;
//图片大小
parameter RR=256;
parameter CC=256;
 
reg i_clk;		 
reg i_rst; 
 
reg i_image_en;
reg[7:0] i_image;
			
wire o_en_1dfft;
wire o_last_1dfft;
wire[19:0] o_image_R1dfft;
wire[19:0] o_image_I1dfft;		
			
			
			
Image_1Dfft Image_1Dfft_u(		
		 .i_clk					(i_clk),
		 .i_rst					(i_rst),
		 .i_image_en		    (i_image_en),
		 .i_image		        (i_image),
		 
		 .o_en_1dfft      		(o_en_1dfft),
		 .o_last_1dfft    		(o_last_1dfft),
		 .o_image_R1dfft        (o_image_R1dfft), 
		 .o_image_I1dfft        (o_image_I1dfft) 
		 );		
		 
		 
wire o_en_1difft;
wire[7:0] o_image_ifft;	
 
Image_1Difft Image_1Difft_u(		
		 .i_clk					(i_clk),
		 .i_rst					(i_rst),
		 .i_image_en		    (o_en_1dfft),
		 .i_Rimage		        (o_image_R1dfft),
		 .i_Iimage		        (o_image_I1dfft),
		 .o_en_1difft      		(o_en_1difft),
		 .o_image_ifft          (o_image_ifft)
		 );
 
		
		
		
initial begin
i_clk  = 1;
i_rst  = 1;
#1000;
i_rst = 0;
end
always #10 i_clk = ~i_clk;	
 
 
//读取图片数据
integer i,j;
reg[15:0]Men_images [(RR*CC-1):0];
initial #500 $readmemh("D:/FPGA_Proj/FPGAtest/codepz/FPGA_image_input.txt",  Men_images);	
 
//将数据保存到txt，用来matlab调用
integer Ifout1;
integer fout2;
initial begin
 Ifout1 = $fopen("EN2.txt","w");
 fout2 = $fopen("IiFFT.txt","w");
end
 
always @ (posedge i_clk)
 begin
 
	
	
   if(o_en_1difft)
	$fwrite(Ifout1,"%d\n",o_en_1difft);
	else
	$fwrite(Ifout1,"%d\n",0);
	
   if(o_en_1difft)
	$fwrite(fout2,"%d\n",o_image_ifft);
	else
	$fwrite(fout2,"%d\n",0);
	
end
endmodule
0X_037m

　　

 

 

 

4.算法理论概述

        基于现场可编程门阵列（Field-Programmable Gate Array, FPGA）实现的图像一维快速傅里叶变换（Fast Fourier Transform, FFT）和逆快速傅里叶变换（Inverse Fast Fourier Transform, IFFT）是数字信号处理领域的重要技术，特别是在图像处理、通信和信号分析等方面有着广泛的应用。

 

 

 

 

 

 

       基于 FPGA 的一维 FFT 和 IFFT 实现，通过高效算法的硬件化，不仅大幅提高了计算速度，而且在功耗和实时性方面展现出优势，特别适合于对计算密集型和实时性要求高的图像处理应用，如图像压缩、图像滤波、图像识别等。