基于BP神经网络的64QAM解调算法matlab性能仿真

1.算法运行效果图预览

 

 

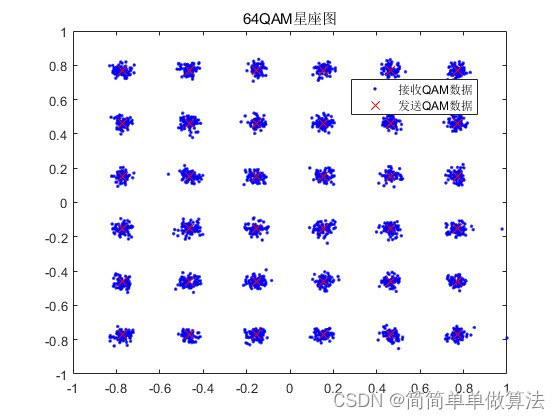
2.算法运行软件版本

MATLAB2022A

 

3.部分核心程序

?

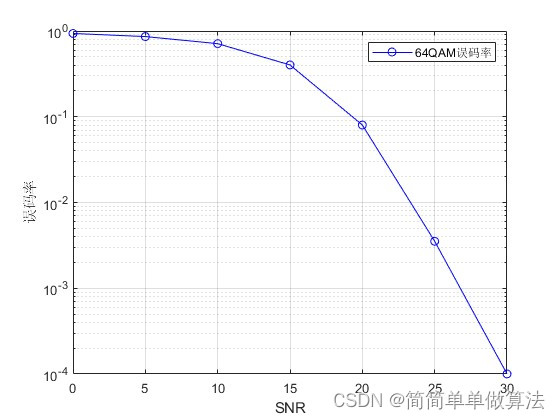
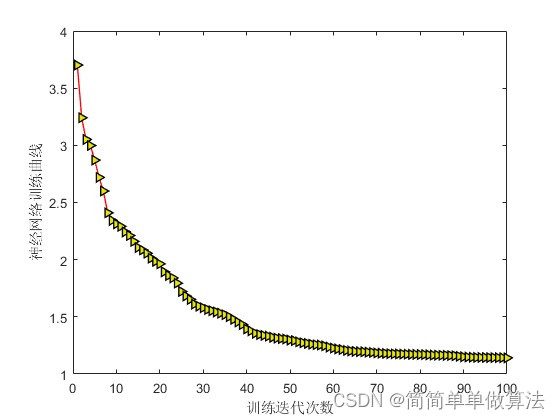
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51

% 第一部分：加载并可视化数据 % load data.mat real1 = [-7 -7 -7 -7 -7 -7 -7 -7 -5 -5 -5 -5 -5 -5 -5 -5 ...          -1 -1 -1 -1 -1 -1 -1 -1 -3 -3 -3 -3 -3 -3 -3 -3 ...          +7 +7 +7 +7 +7 +7 +7 +7 +5 +5 +5 +5 +5 +5 +5 +5 ...          +1 +1 +1 +1 +1 +1 +1 +1 +3 +3 +3 +3 +3 +3 +3 +3 ]./sqrt(42);       imag1 = [-7 -5 -1 -3 +7 +5 +1 +3 -7 -5 -1 -3 +7 +5 +1 +3 ...          -7 -5 -1 -3 +7 +5 +1 +3 -7 -5 -1 -3 +7 +5 +1 +3 ...          -7 -5 -1 -3 +7 +5 +1 +3 -7 -5 -1 -3 +7 +5 +1 +3 ...          -7 -5 -1 -3 +7 +5 +1 +3 -7 -5 -1 -3 +7 +5 +1 +3 ]./sqrt(42);    IQmap = real1'+sqrt(-1)*imag1';    for ij = 1:length(SNR)     ij     for j = 1:20 .......................................................         % 数据划分比例         divT = 0.05; % 训练数据占全部数据的20%         divV = 0.2; % 验证数据占全部数据的10%         % 分割训练集和验证集         SrxT = Srx(1,1:floor(divT*length(Srx)));% 训练集信号         StxT = Stx(1,1:floor(divT*length(Stx)));% 训练集期望结果         SrxV = Srx(1  ,floor(divT*length(Srx))+1:floor((divT+divV)*length(Srx)));% 验证集信号         StxV = Stx(1  ,floor(divT*length(Stx))+1:floor((divT+divV)*length(Stx)));% 验证集期望结果                   [accuracy,yfit] = func_ANN_QAM(Si, Sh, Nlabel, lambda, IQmap, SrxT, StxT, SrxV, StxV);         err(ij,j)=1-accuracy/100;     end end    func_constellation(Srx,Stx,0.5)     figure; semilogy(SNR,mean(err,2),'b-o'); grid on xlabel('SNR'); ylabel('误码率'); legend('64QAM误码率');       figure plot(yfit,'-r>',...     'LineWidth',1,...     'MarkerSize',6,...     'MarkerEdgeColor','k',...     'MarkerFaceColor',[0.9,0.9,0.0]); xlabel('训练迭代次数'); ylabel('神经网络训练曲线'); 143

　　

 

4.算法理论概述

       64QAM是一种高效的数字调制技术，它通过将6个比特映射到64个不同的复数符号上，以实现高数据传输速率。然而，在通信中，由于信道噪声和多径效应，需要解调器恢复原始的比特序列。基于BP（Backpropagation）神经网络的64QAM解调算法，是一种利用神经网络的非线性映射和学习能力，从失真的接收信号中得到原始信号的技术。

 

 

 

      BP神经网络是一种多层前馈网络，通过反向传播算法进行学习和优化。在64QAM解调应用中，神经网络的目标是学习从接收到的失真信号到原始比特序列的映射关系。

 

 

 

       基于BP神经网络的64QAM解调算法，通过神经网络的学习能力，能够有效地从受噪声影响的接收信号中恢复出原始的比特信息，相较于传统的解调方法，它在处理非线性失真和复杂信道条件时表现出了更强的适应性和鲁棒性。