基于CNN+LSTM深度学习网络的时间序列预测matlab仿真,并对比CNN+GRU网络

1.算法运行效果图预览

 

 

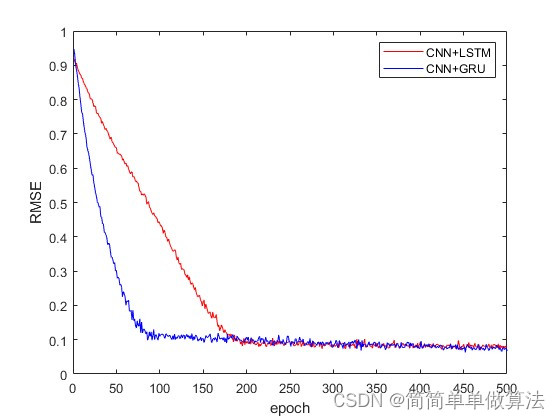
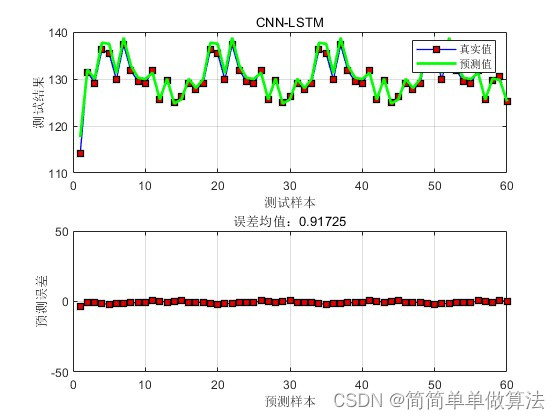
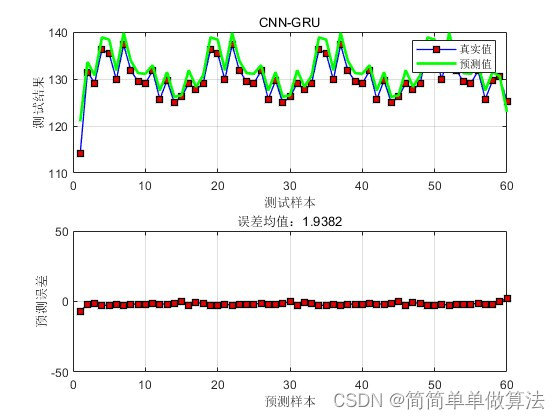
2.算法运行软件版本

MATLAB2022A

 

 

3.算法理论概述

       时间序列预测是数据分析中的一个重要分支，它涉及到对未来事件的预测，基于历史数据中的模式和趋势。在深度学习领域，卷积神经网络（CNN）和循环神经网络（RNN）的组合，特别是结合长短时记忆单元（LSTM）或门控循环单元（GRU），已成为处理时间序列数据的强大工具。

 

3.1 CNN基础

       卷积神经网络（CNN）最初设计用于图像识别，但其强大的特征提取能力同样适用于时间序列数据。CNN通过卷积层捕获局部特征，池化层降低数据维度，从而提取时间序列中的模式。对于一维时间序列数据，卷积操作定义为：

 

 

 

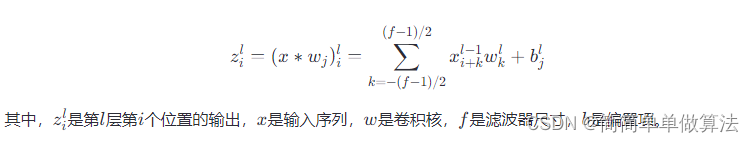
3.2 LSTM原理

        长短时记忆网络（LSTM）是RNN的一种特殊类型，特别擅长处理长序列数据，通过其独特的门机制（输入门、遗忘门、输出门和细胞状态）来控制信息的流动，从而解决了传统RNN中长期依赖问题。LSTM单元的更新可以表示为：

 

 

 

3.3 GRU原理

       门控循环单元（GRU）是LSTM的一个简化版本，它合并了输入门和遗忘门为单一的更新门，同时合并了细胞状态和隐藏状态，减少了模型的复杂性，但仍然能够有效处理长序列数据。GRU的更新公式为：

 

 

 

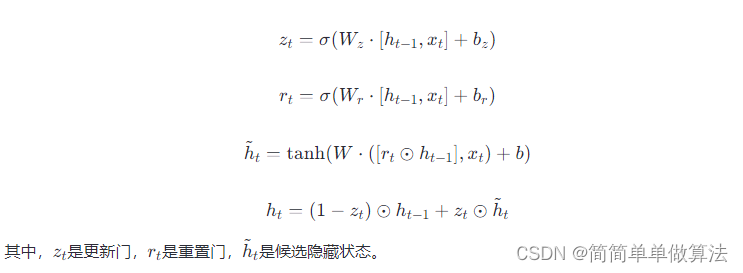
3.4 CNN+LSTM与CNN+GRU对比

共同点：

 

两者的结合都是先通过CNN提取时间序列的局部特征，然后利用RNN（LSTM或GRU）处理序列特征，捕捉长时依赖。

在时间序列预测中，CNN通常用于降维和特征提取，RNN则用于序列建模。

差异：

 

复杂性与计算效率：GRU结构相对简单，参数较少，计算速度较快，适合资源有限的场景。LSTM虽然复杂，但理论上能更好地处理长期依赖问题。

记忆机制：LSTM通过独立的输入门、遗忘门和输出门精细控制信息流动，而GRU通过更新门和重置门合并了这些功能，牺牲了一定的控制精细度，换取了模型的简洁。

应用场景：对于需要细致控制信息遗忘和存储的复杂序列预测任务，LSTM可能更优；而对于追求效率和较简单序列模式识别，GRU可能是更好的选择。

 

 

4.部分核心程序

IT  =[1:length(INFO.TrainingLoss)];
LOSS=INFO.TrainingLoss;
Accuracy=INFO.TrainingRMSE;
 
figure;
plot(IT(1:1:end),LOSS(1:1:end));
xlabel('epoch');
ylabel('LOSS');
 
 
figure;
plot(IT(1:1:end),Accuracy(1:1:end));
xlabel('epoch');
ylabel('RMSE');
 
 
%数据预测
Dpre1 = predict(Net, Nsp_train2);
Dpre2 = predict(Net, Nsp_test2);
 
%归一化还原
T_sim1=Dpre1*Vmax2;
T_sim2=Dpre2*Vmax2;
 
 
figure
subplot(211);
plot(1: Num1, Tat_train,'-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.99,0.4,0.0]);
hold on
plot(1: Num1, T_sim1,'g',...
    'LineWidth',2,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
 
legend('训练样本真实值', '训练样本预测值')
xlabel('预测样本')
ylabel('预测结果')
grid on
 
subplot(212);
plot(1: Num1, Tat_train-T_sim1','-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
 
xlabel('训练样本预测样本')
ylabel('训练样本预测误差')
grid on
ylim([-50,50]);
ERR1=mean(abs(Tat_train-T_sim1'));
title(['误差均值：',num2str(ERR1)]);
figure
subplot(211);
plot(1: Num2, Tat_test,'-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.99,0.4,0.0]);
hold on
plot(1: Num2, T_sim2,'g',...
    'LineWidth',2,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
legend('测试样本真实值', '测试样本预测值')
xlabel('测试样本')
ylabel('测试结果')
grid on
 
subplot(212);
plot(1: Num2, Tat_test-T_sim2','-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
 
xlabel('测试样本预测样本')
ylabel('测试样本预测误差')
grid on
ylim([-50,50]);
ERR2=mean(abs(Tat_test-T_sim2'));
title(['误差均值：',num2str(ERR2)]);
 
save R1.mat