基于BP神经网络的32QAM解调算法matlab性能仿真

1.算法运行效果图预览

 

 

 

2.算法运行软件版本

matlab2022a

 

3.算法理论概述

        32QAM（Quadrature Amplitude Modulation，四相幅度调制）是一种高效的数字调制技术，能够在一个信道内同时传输多比特信息。基于BP（Backpropagation）神经网络的32QAM解调算法，利用神经网络的强大非线性映射能力，直接从接收到的复数信号中估计出原始的调制符号，从而恢复数据。这种方法尤其适用于处理含有噪声、干扰和失真的复杂通信环境。

 

       BP神经网络是一种多层前馈网络，主要包括输入层、隐藏层和输出层。在32QAM解调应用中，网络架构可以如下设计：

 

 

 

        BP神经网络的训练基于梯度下降法，通过最小化损失函数（如交叉熵损失）来更新权重和偏置。训练过程包括以下步骤：

 

 

 

在训练完成后，解调过程简化为前向传播过程：

 

 

 

4.部分核心程序

% 第一部分：加载并可视化数据
real1 = [ 5,-5,5,-5 ,3,-3, 3,-3,...
            5,-5,5,-5, 3,-3, 3,-3,...
            3,-3,3,-3, 1,-1, 1,-1,...
            1,-1,1,-1, 1,-1, 1,-1
]./sqrt(30);
    
 imag1= 1*[-3,-3,3, 3,-3,-3,-5,-5,...
           -1,-1,1, 1,-1,-1, 1, 1,...
            5,5 ,3, 3,-3,-3,-5,-5,...
            5,5, 3, 3,-1,-1, 1, 1
 ]./sqrt(30);  
 
IQmap = real1'+sqrt(-1)*imag1';
 
for ij = 1:length(SNR)
    ij
    for j = 1:20
        
        %为每个神经网络寻找最佳超参数组合
        [accuracy,yfit] = func_ANN_qpsk(Si, Sh, Nlabel, lambda, IQmap, SrxT, StxT, SrxV, StxV);
        err(ij,j)=1-accuracy/100;
    end
end
 
 
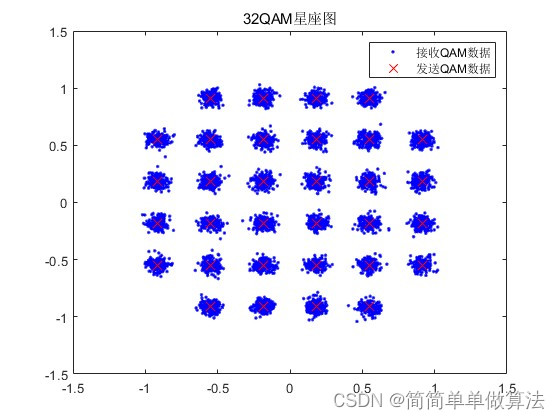
% 调用函数绘制星座图，展示数据的10%
func_constellation(Srx,Stx,0.5)  
 
figure;
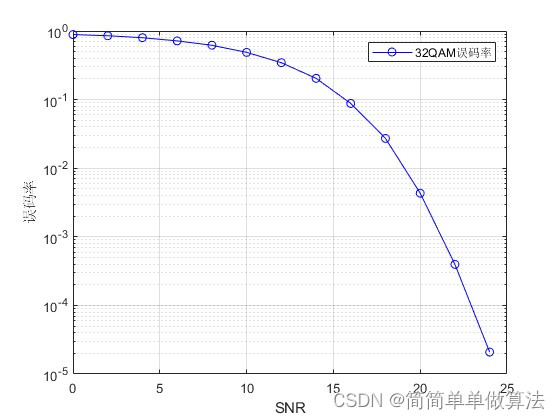
semilogy(SNR,mean(err,2),'b-o');
grid on
xlabel('SNR');
ylabel('误码率');
legend('32QAM误码率');
 
 
figure
plot(yfit,'-r>',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
xlabel('训练迭代次数');
ylabel('神经网络训练曲线');