基于BP神经网络的QPSK解调算法matlab性能仿真

1.算法运行效果图预览

 

 

2.算法运行软件版本

matlab2022a

 

3.算法理论概述

        QPSK（Quadrature Phase Shift Keying）是一种常见的数字调制方式，通过载波的四种相位状态来传输两比特信息。在接收端，准确解调出原始数据成为关键任务。传统的方法如相干解调虽有效但对同步要求较高，而基于BP（Back Propagation）神经网络的解调算法提供了一种自适应、非线性处理手段，尤其适用于复杂信道条件下的解调。

 

       QPSK信号在经过信道传输后，会受到噪声干扰、多径效应等影响，导致星座点偏移或失真，增加了传统解调方法的误码率。BP神经网络以其强大的非线性拟合能力和自适应学习能力，能够学习并补偿这些失真，从而实现更稳健的解调。

 

       假设接收到的QPSK信号为s(t)，经过匹配滤波器后得到基带信号r(t)，通过采样得到离散信号{r[n]}，作为BP神经网络的输入。网络的输出层设计为四个神经元，分别对应QPSK的四种相位状态，输出概率最大的神经元所对应的相位即为解调结果。

 

       设输入层节点数为NI​，隐藏层节点数为NH​，输出层节点数为NO​=4（对应QPSK的四个相位）。网络权重矩阵分别为W(1)（输入到隐藏层）和W(2)（隐藏层到输出层），偏置向量为b(1)和b(2)。

 

       对于输入向量x，第j个隐藏层神经元的激活值aj(1)​计算如下：

 

 

 

       利用已知的QPSK信号样本集对网络进行训练，不断迭代上述过程直至收敛。训练完成后，使用测试集验证网络性能，通过比较解调出的比特序列与原序列的差异来评估误码率(BER)。

 

 

 

 

4.部分核心程序

for ij = 1:length(SNR)
    ij
    for j = 1:20
        % 数据划分比例
        divT = 0.05; % 训练数据占全部数据的20%
        divV = 0.2; % 验证数据占全部数据的10%
        % 分割训练集和验证集
        SrxT = Srx(1,1:floor(divT*length(Srx)));% 训练集信号
        StxT = Stx(1,1:floor(divT*length(Stx)));% 训练集期望结果
        SrxV = Srx(1  ,floor(divT*length(Srx))+1:floor((divT+divV)*length(Srx)));% 验证集信号
        StxV = Stx(1  ,floor(divT*length(Stx))+1:floor((divT+divV)*length(Stx)));% 验证集期望结果
        
        %为每个神经网络寻找最佳超参数组合
        [accuracy,yfit] = func_ANN_qpsk(Si, Sh, Nlabel, lambda, IQmap, SrxT, StxT, SrxV, StxV);
        err(ij,j)=1-accuracy/100;
    end
end
 
 
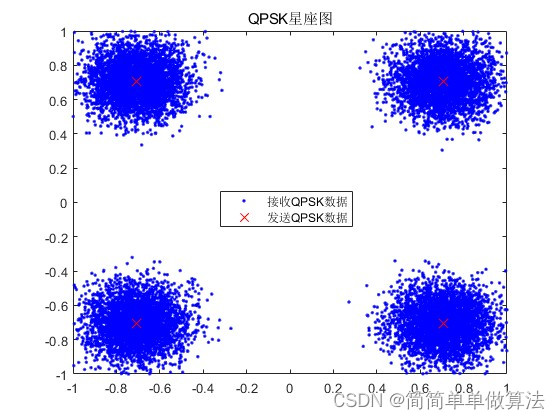
% 调用函数绘制星座图，展示数据的10%
func_constellation(Srx,Stx,0.5)  
 
figure;
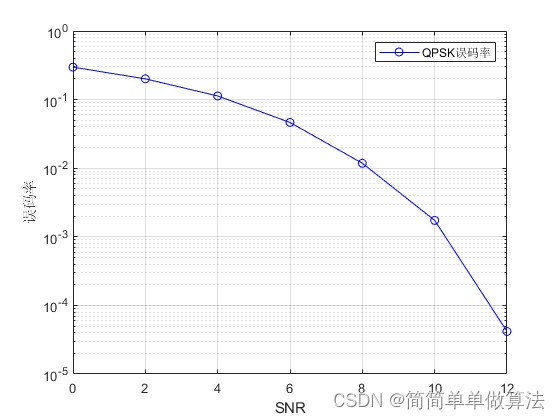
semilogy(SNR,mean(err,2),'b-o');
grid on
xlabel('SNR');
ylabel('误码率');
legend('QPSK误码率');
 
 
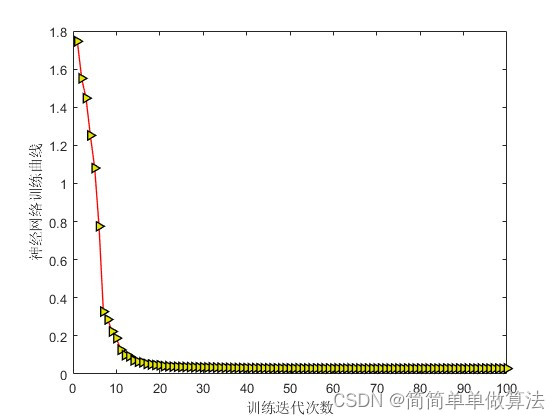
figure
plot(yfit,'-r>',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
xlabel('训练迭代次数');
ylabel('神经网络训练曲线');