基于GWO灰狼优化的CNN-LSTM-Attention的时间序列回归预测matlab仿真
1.算法运行效果图预览
优化前
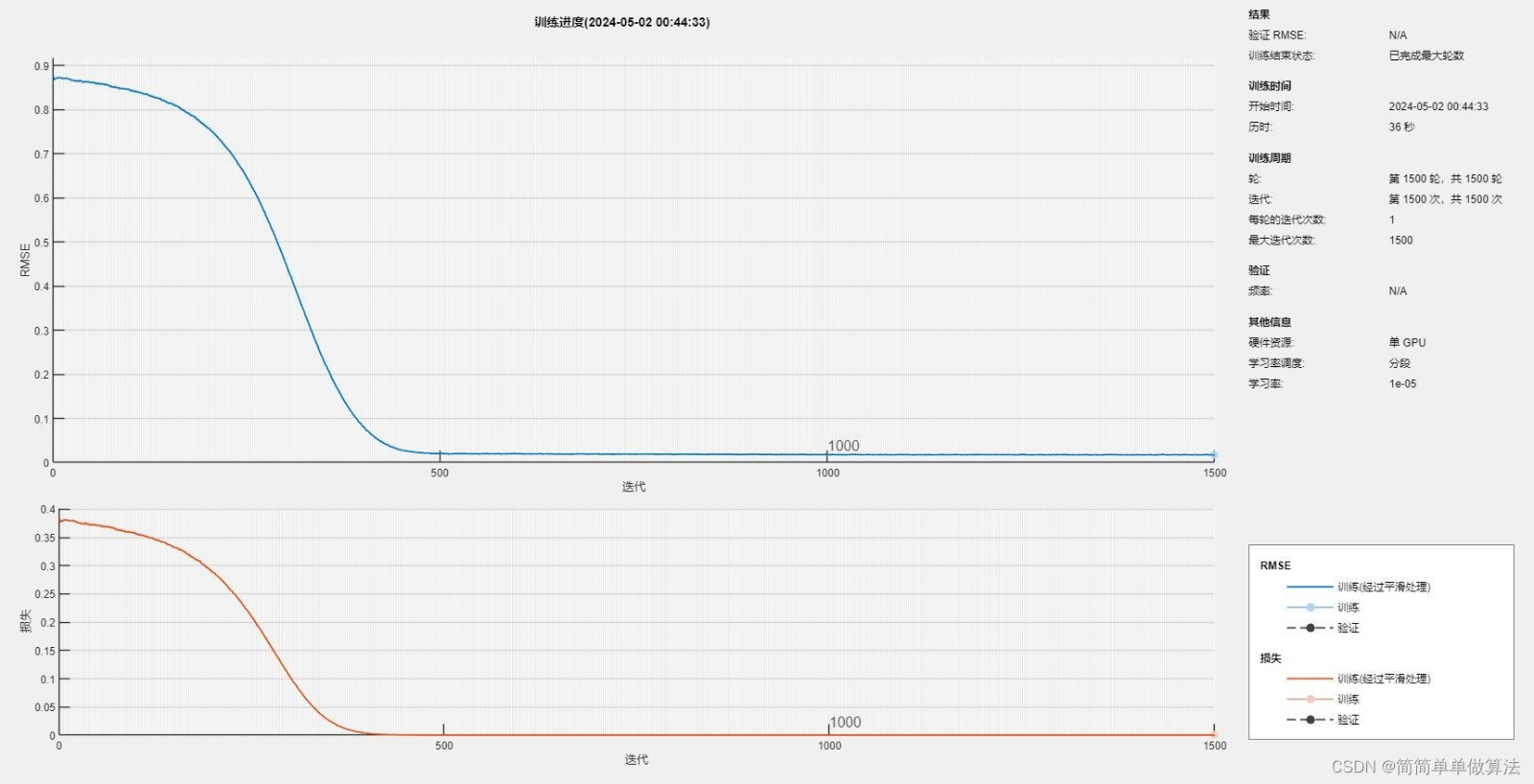
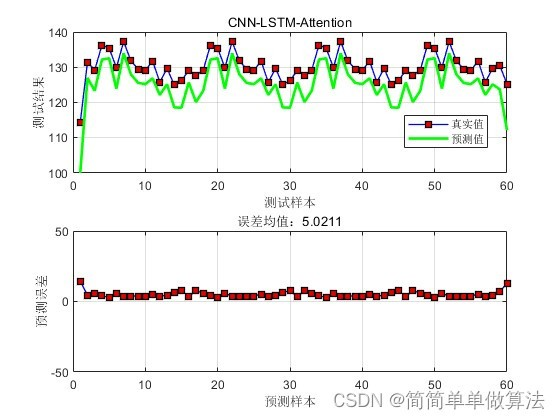
优化后
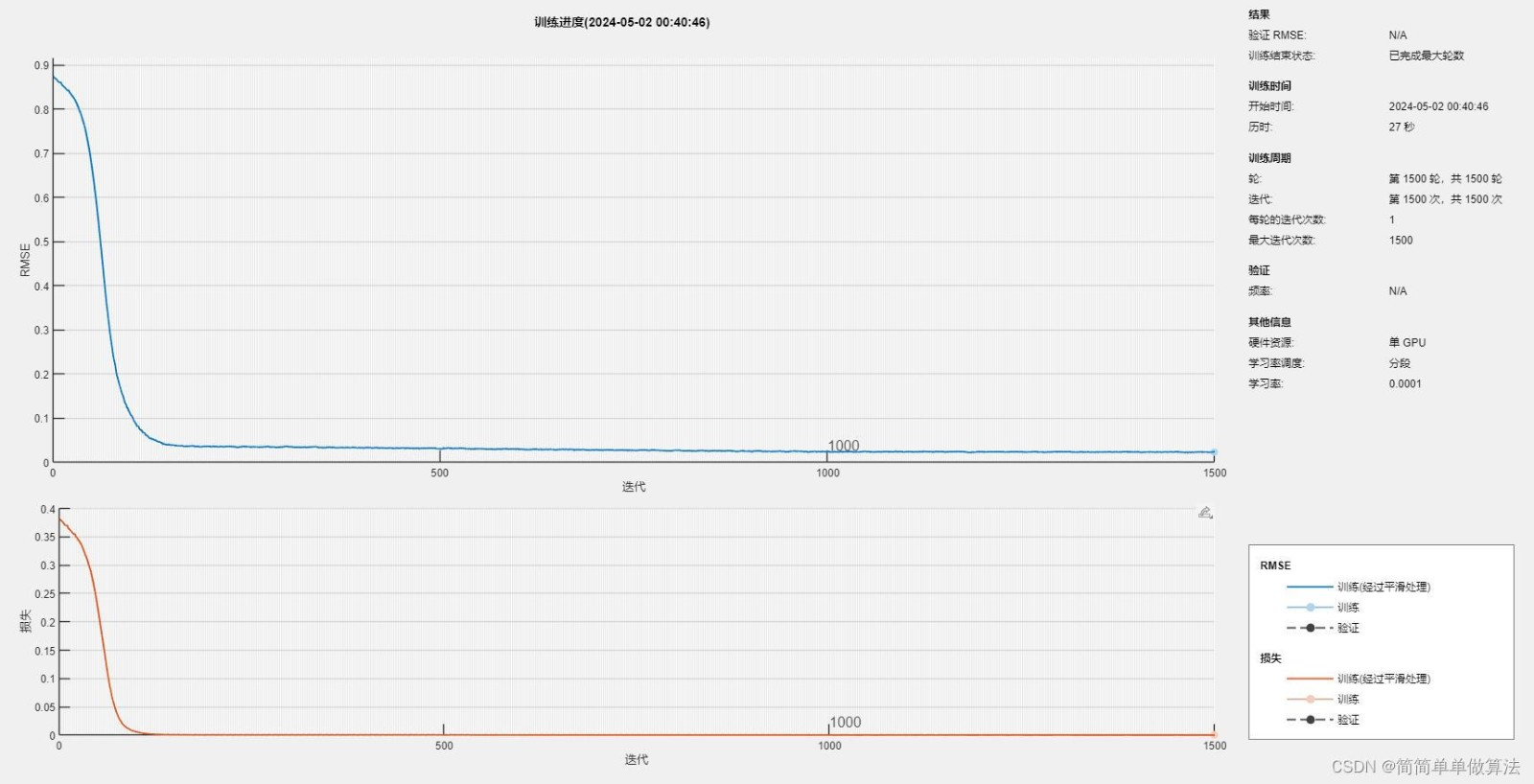
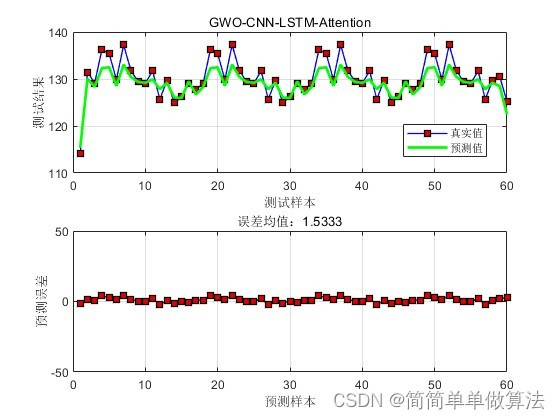
2.算法运行软件版本
matlab2022a
3.算法理论概述
时间序列回归预测是数据分析的重要领域,旨在根据历史数据预测未来时刻的数值。近年来,深度学习模型如卷积神经网络(Convolutional Neural Network, CNN)、长短时记忆网络(Long Short-Term Memory, LSTM)以及注意力机制(Attention Mechanism)在时间序列预测中展现出显著优势。然而,模型参数的有效设置对预测性能至关重要。灰狼优化(GWO)作为一种高效的全局优化算法,被引入用于优化深度学习模型的超参数。
3.1卷积神经网络(CNN)在时间序列中的应用
在时间序列数据中,CNN用于提取局部特征和模式。对于一个长度为T的时间序列数据X = [x_1, x_2, ..., x_T],通过卷积层可以生成一组特征映射:

CNN通过多个卷积层和池化层的堆叠来提取输入数据的特征。每个卷积层都包含多个卷积核,用于捕捉不同的特征。池化层则用于降低数据的维度,减少计算量并增强模型的鲁棒性。
3.2 长短时记忆网络(LSTM)处理序列依赖关系
LSTM单元能够有效捕捉时间序列中的长期依赖关系。在一个时间步t,LSTM的内部状态h_t和隐藏状态c_t更新如下:

长短时记忆网络是一种特殊的循环神经网络(RNN),设计用于解决长序列依赖问题。在时间序列预测中,LSTM能够有效地捕捉时间序列中的长期依赖关系。
3.3 注意力机制(Attention)
注意力机制是一种让模型能够自动地关注输入数据中重要部分的技术。在时间序列预测中,注意力机制可以帮助模型关注与当前预测最相关的历史信息。
CNN-LSTM-Attention模型结合了CNN、LSTM和Attention三种技术的优势。首先,使用CNN提取时间序列中的局部特征;然后,将提取的特征输入到LSTM中,捕捉时间序列中的长期依赖关系;最后,通过注意力机制对LSTM的输出进行加权,使模型能够关注与当前预测最相关的历史信息。具体来说,模型的流程如下:

3.4 GWO优化
灰狼优化(Grey Wolf Optimizer, GWO)是一种受到灰狼社群行为启发的全球优化算法,由Seyedali Mirjalili等于2014年提出。它模仿了灰狼在自然界中的领导层次结构、狩猎策略以及社会共存机制,以解决各种复杂的优化问题。与遗传算法类似,GWO也是基于种群的优化技术,但其独特的搜索策略和更新规则使其在处理某些类型的问题时展现出不同的优势。
在GWO算法中,灰狼被分为四类:α(领头狼)、β(第二领导者)、δ(第三领导者)以及普通狼(Ω)。在每次迭代中,这些角色对应于当前种群中适应度最好的三个解以及其余的解。通过模拟这些狼在捕食过程中的协作与竞争,算法逐步向全局最优解靠近。
4.部分核心程序
a=2*(1-(t/Iters));
for i=1:Num
for j=1:dim
r1 = rand;
r2 = rand;
A1 = 2*a*r1-a;%
C1 = 2*r2; %
D_alpha = abs(C1*Alpx(j)-xpos(i,j));%
X1 = Alpx(j)-A1*D_alpha; %
r1 = rand;
r2 = rand;
A2 = 2*a*r1-a; %
C2 = 2*r2; %
D_beta = abs(C2*btx(j)-xpos(i,j)); %
X2 = btx(j)-A2*D_beta; %
r1 = rand;
r2 = rand;
A3 = 2*a*r1-a; %
C3 = 2*r2; %
D_delta = abs(C3*dltx(j)-xpos(i,j)); %
X3 = dltx(j)-A3*D_delta; %
xpos(i,j) = (X1+X2+X3)/3;%
if xpos(i,j)>=Lmax(j)
xpos(i,j)=Lmax(j);
end
if xpos(i,j)<=Lmin(j)
xpos(i,j)=Lmin(j);
end
end
end
end
LR = Alpx(1)
numHiddenUnits = floor(Alpx(2))+1
........................................................................
%数据预测
Dpre1 = predict(Net, Nsp_train2);
Dpre2 = predict(Net, Nsp_test2);
%归一化还原
T_sim1=Dpre1*Vmax2;
T_sim2=Dpre2*Vmax2;
%网络结构
analyzeNetwork(Net)
figure
subplot(211);
plot(1: Num1, Tat_train,'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
plot(1: Num1, T_sim1,'g',...
'LineWidth',2,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
grid on
subplot(212);
plot(1: Num1, Tat_train-T_sim1','-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
xlabel('预测样本')
ylabel('预测误差')
grid on
ylim([-50,50]);
figure
subplot(211);
plot(1: Num2, Tat_test,'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
plot(1: Num2, T_sim2,'g',...
'LineWidth',2,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
legend('真实值', '预测值')
xlabel('测试样本')
ylabel('测试结果')
grid on
subplot(212);
plot(1: Num2, Tat_test-T_sim2','-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
xlabel('预测样本')
ylabel('预测误差')
grid on
ylim([-50,50]);
save R2.mat Num2 Tat_test T_sim2



 浙公网安备 33010602011771号
浙公网安备 33010602011771号