基于混沌序列的图像加解密算法matlab仿真,并输出加解密之后的直方图

1.算法运行效果图预览

 

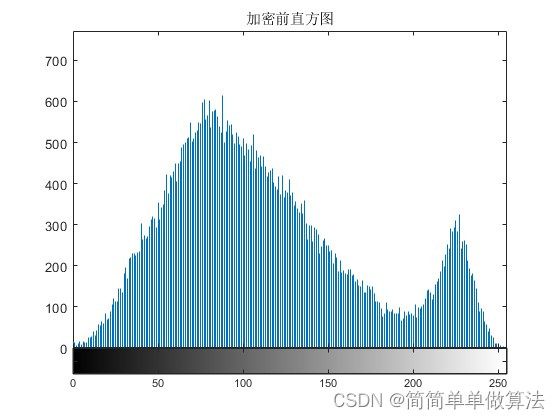
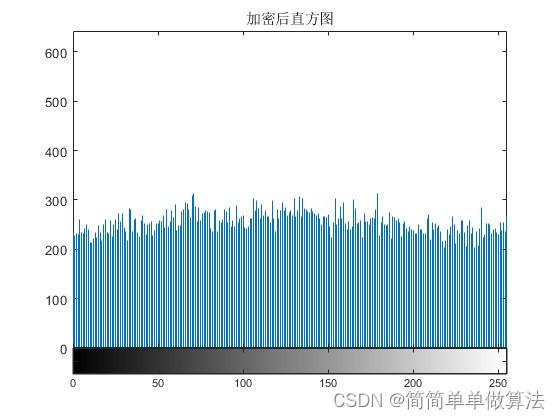
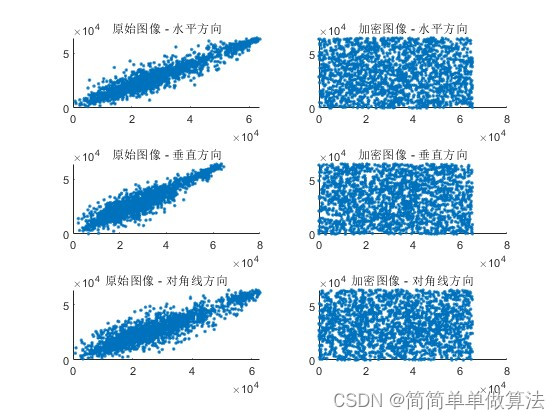
2.算法运行软件版本

matlab2022a

 

3.算法理论概述

3.1 混沌系统特性

        混沌系统是一类具有确定性、非线性、初值敏感性、遍历性和伪随机性等特性的动力学系统。其主要特性包括：

 

确定性：混沌系统由一组确定性微分方程或差分方程描述，不存在随机成分。

 

非线性：混沌系统中至少存在一个非线性项，这是产生混沌现象的必要条件。

 

初值敏感性：混沌系统对初始条件极其敏感，微小的初值变化会导致长期行为的巨大差异，即著名的“蝴蝶效应”。

 

遍历性：在一定条件下，混沌系统的状态将在其相空间中遍历几乎所有的点，具有类似于随机过程的统计特性。

 

伪随机性：混沌序列在统计特性上与真随机序列难以区分，可作为高质量的伪随机数生成器。

 

3.2混沌序列生成

       常用的混沌系统模型包括Logistic映射、Henon映射、Lorenz系统、Chen系统等。以Logistic映射为例，其迭代方程为：

 

 

 

其中xn​ 是第 n 时刻的系统状态，μ 是控制参数。对于适当的 μ 值（如3.57<μ<4），Logistic映射会产生混沌序列。

 

3.3图像加解密流程

基于混沌序列的图像加解密算法一般包括以下几个步骤：

 

图像预处理：将待加密的图像转换为适合处理的数据格式，如灰度图像、二维矩阵等。

 

混沌序列生成：利用选定的混沌系统模型生成足够长度的混沌序列。

 

图像数据混淆：使用混沌序列对图像数据进行重新排列，实现像素位置的随机化，以破坏图像的空间结构信息。常见的混淆方法包括使用混沌序列对像素索引进行排序、轮换等操作。

 

图像数据扩散：利用混沌序列对图像数据进行数值变换，实现像素值的随机化，以破坏图像的统计特性。常见的扩散方法包括混沌序列与图像像素值进行异或、模加、逻辑运算等。

 

密钥生成与管理：混沌系统的参数（如Logistic映射中的μ）和初值共同构成加密密钥。在实际应用中，需要对密钥进行妥善管理和分发，以确保加解密过程的一致性。

 

3.4 加解密算法设计

 

 

4.部分核心程序

% 开始混淆过程
timg = timg(:); % 将图像数据转置为一维向量
for m = 1:size(timg,1)
    t1           = timg(m);
    timg(m)      = timg(idx(m)); % 使用排序索引来重新排列图像像素
    timg(idx(m)) = t1;
end% 结束混淆过程
 
% 创建扩散密钥
p    = 3.628;
k(1) = 0.632;
for n=1:s-1
    k(n+1) = cos(p*acos(k(n))); % 生成混沌序列
end
 
% 将混沌序列量化为整数，并限制在 [0,255] 范围内
k     = abs(round(k*255));
% 将混沌序列转化为二进制形式
k_tmp = de2bi(k);
% 对二进制序列进行循环位移操作
k_tmp = circshift(k_tmp,1);
% 将位移后的二进制序列转回十进制形式，并转置
k_tmp = bi2de(k_tmp)';
% 计算异或密钥
key   = bitxor(k,k_tmp);
% 结束扩散密钥的创建
% 开始最终加密过程
timg  = timg'; % 将图像数据转置回二维矩阵形式
timg  = bitxor(uint8(key),uint8(timg)); % 对图像像素与密钥进行异或操作
himg  = reshape(timg,[RR CC]); % 重塑加密后的图像数据为原图像尺寸