基于EKF扩展卡尔曼滤波的传感器网络目标跟踪matlab仿真

1.算法运行效果图预览

 

 

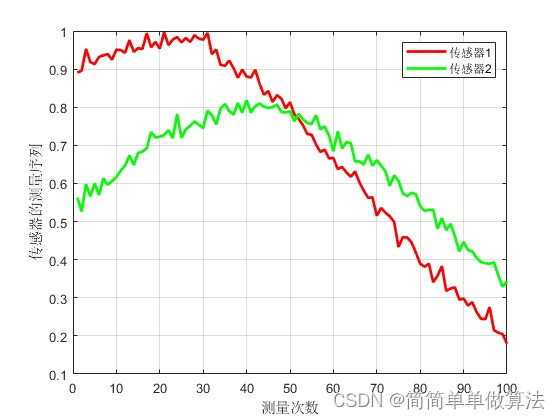
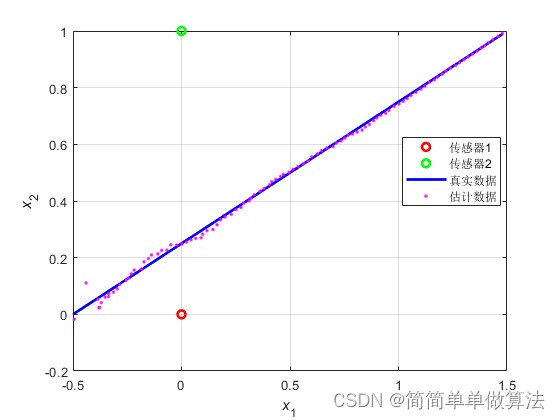
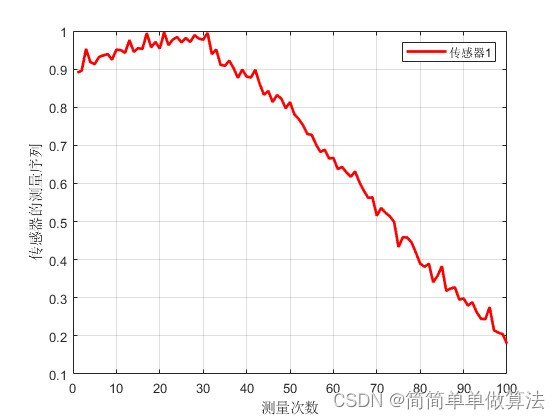
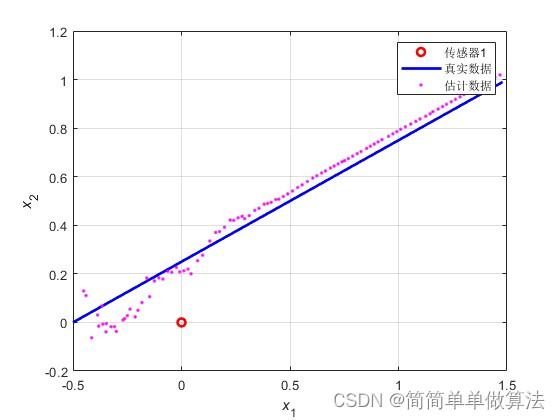
2.算法运行软件版本

MATLAB2022a

 

3.算法理论概述

        随着传感器网络技术的不断发展，目标跟踪作为其核心应用之一，在军事、民用等领域中得到了广泛的关注。扩展卡尔曼滤波（EKF）作为一种有效的非线性滤波方法，被广泛应用于传感器网络的目标跟踪中。

 

       传感器网络是由分布在空间中的多个传感器节点组成，这些节点通过无线通信方式相互连接，共同协作完成对环境信息的感知、处理和传输。目标跟踪是指利用传感器网络获取的目标状态信息（如位置、速度等），通过一定的算法估计目标的运动状态，并实现对目标未来运动状态的预测。

 

       在传感器网络目标跟踪中，由于传感器节点的观测数据通常受到噪声干扰和非线性因素的影响，因此需要采用有效的滤波算法对观测数据进行处理，以提高目标跟踪的精度和鲁棒性。扩展卡尔曼滤波（EKF）正是一种适用于非线性系统的滤波方法，它通过对非线性系统进行线性化近似处理，再利用标准卡尔曼滤波框架进行状态估计和预测。

 

        扩展卡尔曼滤波是一种处理非线性系统状态估计的方法，它通过线性化非线性过程和测量模型，在每次迭代中利用高斯分布的性质进行最优估计。

 

 

 

 

 

 

       在多传感器网络环境下，每个传感器可能提供关于目标的不同视角或不同属性的观测数据。每个传感器节点都独立运行一个EKF，然后通过数据融合技术（如卡尔曼融合或分布式卡尔曼滤波）整合所有传感器的信息来获取更准确的目标状态估计。

 

 

 

 

4.部分核心程序

% 定义初始位置的均值和标准差  
Xreal0 = [-0.5; 0];
sgm0   = sqrt(0.05);
% 初始化估计位置，加入随机噪声 
XNreal0= Xreal0 + sgm0 * randn(2, 1); % posicion inicial estimada
% 初始化估计位置矩阵  
Xst    = zeros(2, MTKL);
Xst(:, 1) = XNreal0; 
% 初始化位置协方差矩阵  
P_t       = sgm0^2 * eye(size(Xst, 1)); 
% 定义u的协方差矩阵 
Q         = 0; 
% 定义测量噪声的协方差矩阵  
R         = sgm^2 * eye(size(Pxy, 2));  
% 初始化f向量 
f         = zeros(size(Pxy, 2), 1);
% Kalman 滤波循环  
for t = 2 : MTKL 
    % 预测步骤  
    Xst1 = A * Xst(:, t - 1) + u;  % 预测位置
    Pst1 = Q + A * P_t * A';% 预测协方差  
    
    % 更新步骤
    J   = func_jacob(Xst1, Pxy);% 计算雅可比矩阵  
    K_t = Pst1 * J'/(J * Pst1 * J' + R);    % 计算Kalman增益 
    for i = 1 : length(f)
        f(i) = exp(-0.5 * norm(Xst1 - Pxy(:, i))^2);% 计算预测的测量值  
    end
    % 更新估计位置  
    Xst(:, t) = Xst1 + K_t * (Yr(:, t) - f);
    % 更新协方差
    P_t       = Pst1 - K_t * (J * Pst1 * J') * K_t';
end
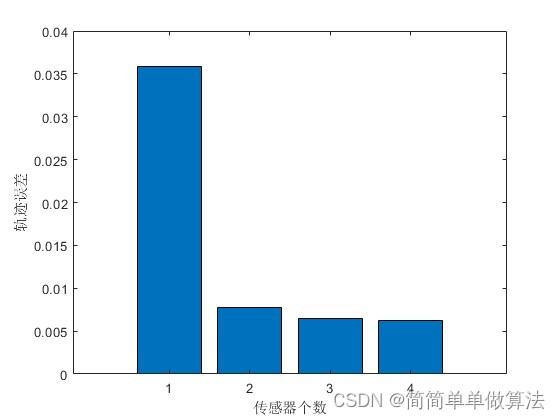
err= mean2(abs(Xr0-Xst))
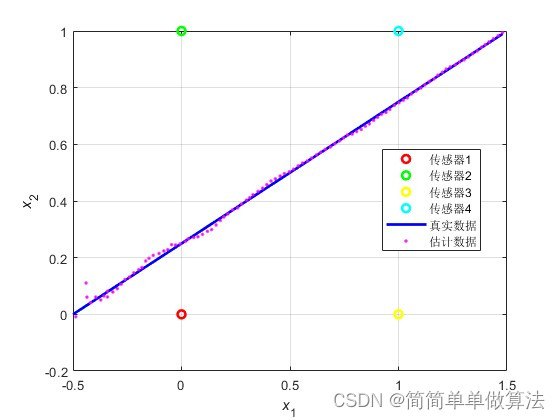
% 绘制传感器位置、真实轨迹和估计轨迹 
figure
plot(Pos1(1), Pos1(2), 'ro', 'LineWidth', 2);
hold on
plot(Pos2(1), Pos2(2), 'go', 'LineWidth', 2);
hold on
plot(Pos3(1), Pos3(2), 'yo', 'LineWidth', 2);
hold on
plot(Pos4(1), Pos4(2), 'co', 'LineWidth', 2);
hold on
plot(Xr0(1, :), Xr0(2, :), 'b', 'LineWidth', 2);
hold on
plot(Xst(1, :), Xst(2, :), 'm.', 'LineWidth', 1);
xlabel('{\itx}_{1}'), 
ylabel('{\itx}_{2}');
legend('传感器1', '传感器2', '传感器3', '传感器4', '真实数据', '估计数据');
grid;
save R1.mat err