基于Mamdani模糊神经网络的调速控制系统simulink建模与仿真

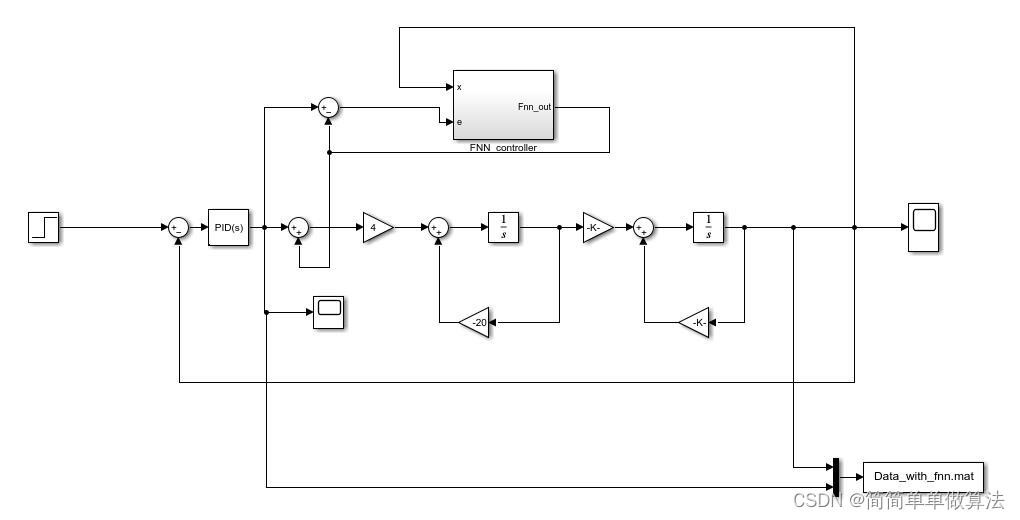
1.算法运行效果图预览

 

 

 

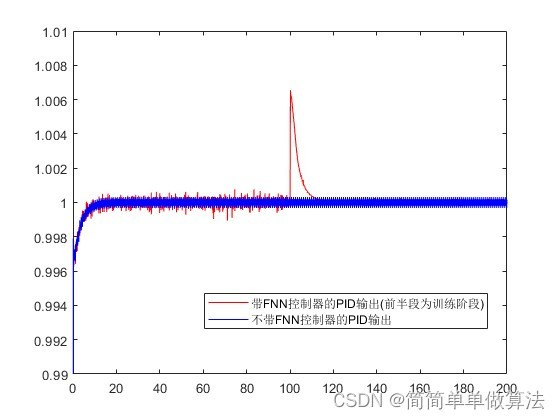
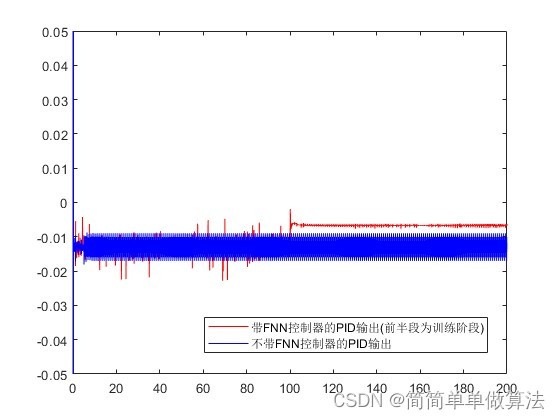
2.算法运行软件版本

matlab2022a

 

3.算法理论概述

       基于Mamdani模糊神经网络的调速控制系统是一种结合模糊逻辑与神经网络技术的智能控制方法，旨在提高调速系统的性能。随着工业技术的不断发展，对调速控制系统的性能要求也越来越高。传统的控制方法往往难以处理非线性、时变和不确定性等问题。而基于Mamdani模糊神经网络的调速控制系统通过结合模糊逻辑和神经网络的优点，能够有效地解决这些问题，提高调速系统的稳定性和动态性能。

 

3.1 模糊神经网络控制器概述

        模糊逻辑是一种处理不确定性和模糊性的数学工具，它允许变量在0和1之间取任意值，表示属于某个集合的程度。在调速控制系统中，模糊逻辑可以用来描述电机转速的模糊状态，如“低速”、“中速”和“高速”等。模糊集合是模糊逻辑的基本概念，它表示一个对象属于某个集合的程度。隶属度函数用来描述对象属于模糊集合的程度，通常表示为μ(x)，其中x为对象，μ(x)为隶属度，取值范围为[0,1]。

       模糊推理是根据模糊规则进行推理的过程。在调速控制系统中，模糊规则可以表示为“如果电机转速为低速，则增加电机电压”，其中“低速”和“增加电机电压”都是模糊概念。通过模糊推理，可以得到控制量的模糊值。

 

       神经网络是一种模拟人脑神经元连接方式的计算模型，具有强大的自学习和自适应能力。在调速控制系统中，神经网络可以用来逼近非线性函数和优化控制参数。神经网络由多个神经元组成，通常分为输入层、隐藏层和输出层。在调速控制系统中，输入层接收电机转速等状态变量，输出层产生控制量，隐藏层用来逼近非线性函数。

 

       基于Mamdani模糊神经网络的调速控制系统结合了模糊逻辑和神经网络的优点，既能处理模糊性和不确定性问题，又具有自学习和自适应能力。该系统主要由以下几个部分组成：

 

输入变量模糊化：将电机转速等输入变量通过隶属度函数转换为模糊变量。

模糊推理：根据预先设定的模糊规则进行推理，得到控制量的模糊值。

神经网络逼近：利用神经网络逼近非线性函数，优化控制参数。

去模糊化：将模糊控制量通过去模糊化方法转换为实际的控制量。

控制执行：将实际的控制量作用于电机，实现调速控制。

 

3.2 模糊神经网络控制器基本原理

       由于模糊控制是建立在专家经验的基础之上的，但这有很大的局限性，而人工神经网络可以充分逼近任意复杂的时变非线性系统，采用并行分布处理方法，可学习和自适应不确定系统。利用神经网络可以帮助模糊控制器进行学习，模糊逻辑可以帮助神经网络初始化及加快学习过程。

 

       通常神经网络的基本构架如下所示：

 

 

 

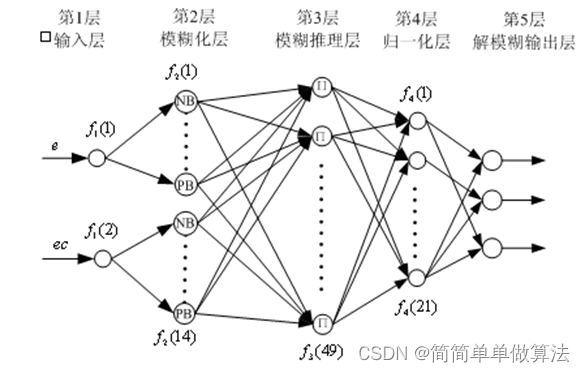
第一层为输入层，其主要包括两个节点，所以第一层神经网络的输入输出可以用如下的式子表示：

 

 

 

第二层为输入变量的语言变量值，通常是模糊集中的n个变量，它的作用是计算各输入分量属于各语言变量值模糊集合的隶属度。用来确定输入在不同的模糊语言值对应的隶属度，以便进行模糊推理，如果隶属函数为高斯函数，那么其表达式为：

 

 

 

第三层是比较关键的一层，即模糊推理层，这一层的每个节点代表一条模糊规则，其每个节点的输出值表示每条模糊规则的激励强度。该节点的表达式可用如下的式子表示：

 

 

 

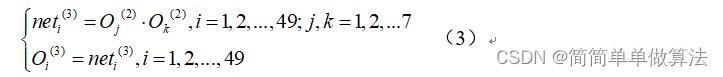
第四层为归一化层，其输出是采用了Madmdani模糊规则，该层的表达式为：

 

 

 

第五层是模糊神经网络的解模糊层，即模糊神经网络的清晰化.

 

 

 

 

4.部分核心程序

 

Feedfor_phase;
%定义整个模糊神经网络的各个层的数据状态
%第一层
x       = u(1:Number_inport);
In1     = x*ones(1,Number_Fuzzy_rules);%第一层的输入
Out1    = 1./(1 + (abs((In1-mean1)./sigma1)).^(2*b1));%第一层的输出，这里，这个神经网络的输入输出函数可以修改
%第一层
precond = Out1'; 
Out2    = prod(Out1)';
S_2     = sum(Out2);%计算和
%第三层
if S_2~=0
   Out3 = Out2'./S_2;
else
   Out3 = zeros(1,NumRules);%为了在模糊控制的时候方便系统的运算，需要对系统进行归一化处理
end
%第四层
Aux1    = [x; 1]*Out3;
a       = reshape(Aux1,(Number_signal_in+1)*NumRules,1);%控制输出
%第五层，最后结果输出
outact  = a'*ThetaL4;
%最后的出处结果
out     = [outact;Xt];             
else
out     = [];
end