通信系统中ZF,ML,MRC以及MMSE四种信号检测算法误码率matlab对比仿真

1.算法运行效果图预览

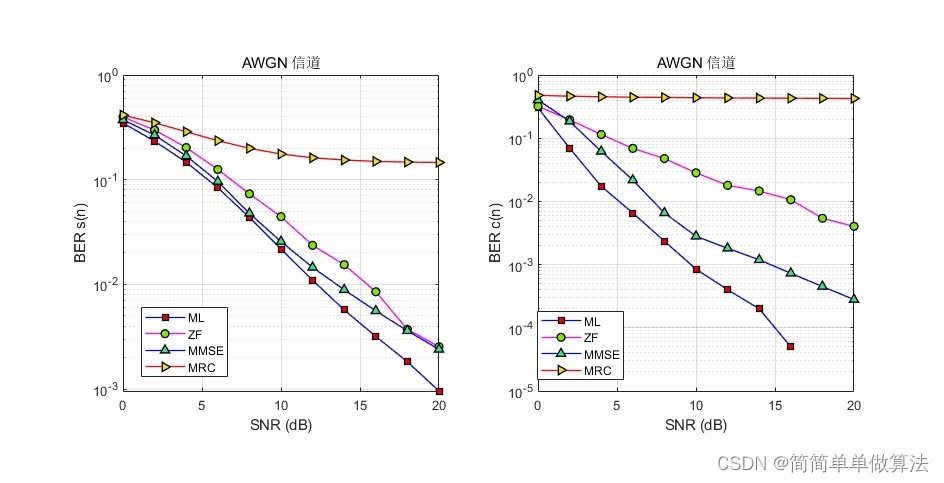
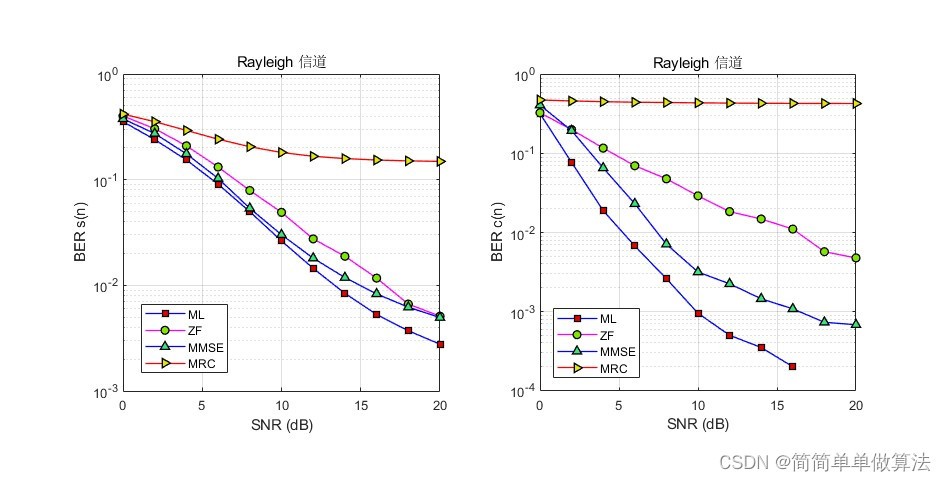
2.算法运行软件版本

matlab2022a

3.算法理论概述

通信系统中ZF（Zero Forcing，零迫）、ML（Maximum Likelihood，最大似然）、MRC（Maximum Ratio Combining，最大比合并）和MMSE（Minimum Mean Square Error，最小均方误差）是四种常见的信号检测算法。这些算法在通信系统中用于从接收信号中恢复出原始发送信号。

3.1、ZF（零迫）算法

ZF算法是一种简单的信号检测算法，它的目标是在接收端完全消除干扰和噪声，从而恢复出原始的发送信号。ZF算法通过迫零接收端的干扰和噪声，使得接收信号只包含所需的信号分量。

假设接收信号为y，发送信号为s，信道矩阵为H，噪声为n，则接收信号可以表示为：

y = Hs + n

ZF算法通过左乘信道矩阵的逆矩阵H^(-1)，得到：

s = H^(-1) * y

这样，就可以恢复出原始的发送信号s。

3.2、ML（最大似然）算法

ML算法是一种基于统计学的信号检测算法，它的目标是在所有可能的发送信号中，找到最有可能的那一个。ML算法通过比较接收信号与所有可能的发送信号的似然度，选择似然度最大的那个作为最终的检测结果。

假设发送信号有M种可能，每种可能的概率为p(s|y)，则ML算法的目标是找到使得p(s|y)最大的s。具体的数学表达式为：

s_ML = arg max p(s|y)

3.3、MRC（最大比合并）算法

MRC算法是一种多天线技术中的信号检测算法，它的目标是通过合并多个接收天线的信号，提高接收信号的信噪比。MRC算法通过对每个接收天线的信号进行加权合并，使得合并后的信号信噪比最大化。

假设有N个接收天线，每个天线的接收信号为y_n，信道为h_n，噪声为n_n，则MRC算法的输出可以表示为：

y_MRC = Σ (h_n^* * y_n) / Σ |h_n|^2

其中，*表示共轭运算。

3.4、MMSE（最小均方误差）算法

MMSE算法是一种考虑噪声和干扰的信号检测算法，它的目标是在抑制噪声和干扰的同时，尽可能地减小误差。MMSE算法通过最小化均方误差来衡量检测性能的优劣。

假设接收信号为y，发送信号为s，信道矩阵为H，噪声为n，则MMSE算法的输出可以表示为：

s_MMSE = (H^H * H + σ^2 * I)^(-1) * H^H * y

其中，σ^2是噪声的方差，I是单位矩阵。

以上是ZF、ML、MRC和MMSE四种信号检测算法的原理和数学公式。这些算法在通信系统中有着广泛的应用，可以提高通信系统的性能和稳定性。

4.部分核心程序

N              = 100;                            %Tc/TS the ratio between symbol period
num_Source_bit = 2e6;          %1000000
num_Tag_bit    = num_Source_bit/N;%10000
num_Channel    = num_Source_bit/f_s;%100
  
s_Alphabet     = 1/sqrt(2)* [1+1j;-1+1j ;-1-1j ;1-1j];%4x1
c_Alphabet     = [1;-1];                              %2x1
  
s_Matrix       = exp(j*(randi([0 3],num_Channel,f_s)*pi/2+pi/4));      %ambient signal (QPSK)             %100x10000
c_Matrix       = 2*(randi([0 1],num_Channel,f_s/N))-1;                     %backscattered signal (BPSK)   %100x100
noise_Matrix   = 1/sqrt(2)* (normrnd(0,sqrt(varNoise),num_Channel,f_s) + 1i*normrnd(0,sqrt(varNoise),num_Channel,f_s));%100x10000
  
%% AWGN
for kChannel = 1:num_Channel%100
    kChannel
    h = 1/sqrt(2)*(normrnd(0,1) + 1i*normrnd(0,1));         %normalized direct-link channel
    f = 1/sqrt(2)*(normrnd(0,1) + 1i*normrnd(0,1));          %normalized TX-Tag channel
    g = sqrt(0.5);                                                             %fixed Tag-C-RX channel
    s = s_Matrix(kChannel,:);%%S-matrix:100x10000 ; S：1x10000                                           
    c = c_Matrix(kChannel,:);%c-matrix:100x100 ; c：1x100
    noise = noise_Matrix(kChannel,:);%noise:1x10000
    c_sample = reshape(repmat(c,N,1),1,f_s);%fs=1e4 thus,repmat(c,N,1)：100x100;c-sample：1x10000
     
    for kSNR = 1:length(SNR_dB)%length=11
        p     = P(kSNR);
        y     = sqrt(p)*h*s + sqrt(p)*f*alpha*g*s.*c_sample; %1x10000 received signal
        y_std = sqrt(p)*h*s;
        y     = awgn(y,SNR_dB(kSNR),'measured');
        y_std = awgn(y_std,SNR_dB(kSNR),'measured');
         
        %%ML detection 
        %%fixed c=-1
        s_detection_c1     = abs( repmat(y,4,1)- sqrt(p)*(h -  alpha * g * f)* repmat(s_Alphabet,1,f_s));
        [~,s_Est_c1_index] = min(s_detection_c1);
        s_Est_c1           = exp(j*(mod(s_Est_c1_index-1,4)*pi/2+pi/4));
        %%fixed c=1
        s_detection_c2     = abs( repmat(y,4,1)- sqrt(p)*(h +  alpha * g * f)* repmat(s_Alphabet,1,f_s));
        [~,s_Est_c2_index] = min(s_detection_c2);
        s_Est_c2           = exp(j*(mod(s_Est_c2_index-1,4)*pi/2+pi/4));
         
         
        c_detection        = abs([y-sqrt(p)*(h-alpha * g * f)*s_Est_c1; y-sqrt(p)*(h+ alpha * g * f)*s_Est_c2]).^2;
        c_est_block1       = sqrt(sum(reshape(c_detection(1,:),N,f_s/N)));
        c_est_block2       = sqrt(sum(reshape(c_detection(2,:),N,f_s/N)));
         
        [~,c_Est_index]    = min([c_est_block1;c_est_block2]);
        c_Est              = (c_Est_index-1)*2-1;
         
         
        c_Est_sample       = reshape(repmat(c_Est,N,1),1,f_s);%1x10000
        s_detection        = abs( repmat(y,4,1)- sqrt(p)*(h*repmat(s_Alphabet,1,f_s) + s_Alphabet*alpha * g * f*c_Est_sample));
         
        [~,s_Est_index]    = min(s_detection);
        s_Est              = exp(j*(mod(s_Est_index-1,4)*pi/2+pi/4));
  
         
        Num_BER_s(kChannel,kSNR)     = length(find(s-s_Est~=0)); 
        Num_BER_c(kChannel,kSNR)     = length(find(c-c_Est~=0)); 
    end
end
  
num_BER_s     = sum(Num_BER_s);
num_BER_c     = sum(Num_BER_c);
  
  
BER_s     = num_BER_s/num_Source_bit;
BER_c     = num_BER_c/num_Tag_bit;
  
  
figure;
semilogy(SNR_dB,BER_s,'b-o')
hold on
semilogy(SNR_dB,BER_c,'r-s')            
grid on
xlabel('SNR (dB)')
ylabel('BER')
  
legend('s(n)','c(n)')
  
save ML_Awgn.mat SNR_dB BER_s BER_c