基于OFDM+QPSK的通信系统误码率matlab仿真,对比不同同步误差对系统误码率的影响

1.算法运行效果图预览

 

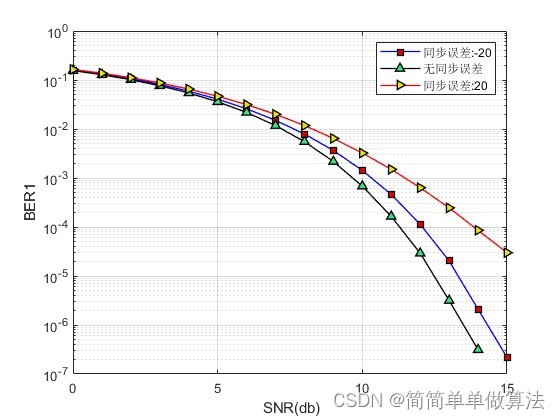
2.算法运行软件版本

MATLAB2022A

 

3.算法理论概述

1.1 OFDM 原理

         OFDM 是一种多载波调制技术，将高速数据流分成多个低速数据流，每个低速数据流用不同的正交子载波传输，从而提高了频谱利用率和抗多径衰落的能力。

 

1.2 QPSK 原理

        QPSK 是一种基于相位的调制方式，将每两个连续的比特映射到不同的相位状态，实现数据的传输。

 

1.3 同步误差对系统性能的影响

        同步误差是指接收端时钟与发送端时钟之间的时间偏移，它可能由于时钟漂移、频率偏差、采样时刻的不准确等原因引起。在 OFDM 系统中，同步误差会导致接收端无法准确地解析每个子载波的相位和幅度，从而影响信号的解调和数据的正确解析。

 

       同步误差会导致解调时的相位和幅度失配，从而增加信号的误码率。特别是在高信噪比条件下，同步误差对误码率的影响更为显著，因为此时信号的主要误差源来自同步误差。

 

        同步误差引起的频偏和相位失配会导致解调后的信号失真。失真的信号可能无法正确解析，甚至无法通过信号解析器，从而造成严重的通信质量问题。

 

 

4.部分核心程序

 for ij3=[-20,0,20]  % 同步误差
    
        if Pilot_OFDM(1) == -1 
           H = exp(1i*2*pi*[1:NFFT]*ij3/NFFT);
           HInv = 1./H;
        end
 
        for snr = SNRs
 
            Rdata = awgn(Subframe,snr,'measured'); % 添加 AWGN 噪声
 
             for ij4 = 0:NSymbol-1
                 OFDMSymbol     =  Rdata(ij4*(OFDMSymLen)+1: (ij4+1)*OFDMSymLen);     
                 if ij3 <= 0  
                    OFDM_Sym_cp = OFDMSymbol(CPLen+1+ij3:OFDMSymLen+ij3); 
                 else 
                    OFDM_Sym_cp =[OFDMSymbol(CPLen+1+ij3:OFDMSymLen) zeros(1,ij3)];
                 end
                 QPSK_Sym = (fft(OFDM_Sym_cp,NFFT)/sqrt(NFFT));
                 %信道估计使用导频符号
                 if sum(ij4 == Pilot_OFDM) && Pilot_OFDM(1) ~= -1
                    H             = zeros(1,NFFT);
                    H(Loc_Pilot)  = (QPSK_Sym(Loc_Pilot)/PilotSymbol);
                    H(find(H==0)) = interp1(Loc_Pilot,H(Loc_Pilot),find(H==0));
                    HInv          = 1./H;
                 end
                
                 QPSK_Sym = HInv.*QPSK_Sym ./ (abs(HInv));
                 if sum(ij4 == Pilot_OFDM)&& Pilot_OFDM(1) ~= -1 
                    QPSK_Sym2 = QPSK_Sym(Loc_Carriers);
                 else
                    QPSK_Sym2 = QPSK_Sym(Data_Carriers);
                 end
        end
        Index = 1;
        BER2    = [BER2;BER1 ];
        plotIdx = plotIdx+1;
    end
    BER3= BER3+BER2;   
end
 
figure;
semilogy(SNRs,BER3(1,:)/1000,'-bs',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
semilogy(SNRs,BER3(2,:)/1000,'k-^',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.2,0.9,0.5]);
hold on
semilogy(SNRs,BER3(3,:)/1000,'-r>',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
hold on
xlabel(' SNR(db)');
ylabel(' BER1 ');
legend('同步误差:-20','无同步误差','同步误差:20');
grid on