基于Fringe-Projection环形投影技术的人脸三维形状提取算法matlab仿真
1.算法运行效果图预览


2.算法运行软件版本
matlab2022a
3.算法理论概述
人脸三维形状提取是计算机视觉和人工智能领域中的重要研究方向。它通过对人脸进行深度信息的获取和分析,得到人脸在三维空间中的几何形状。其中,基于Fringe-Projection环形投影技术的人脸三维形状提取算法是一种常用的非接触式三维扫描方法。
1、数学原理:
Fringe-Projection环形投影技术:
Fringe-Projection环形投影技术是一种基于结构光原理的三维扫描方法。该方法利用投影仪投射环形光条(条纹)到目标物体表面,通过相机捕获投影物体的图像,然后根据条纹的形变信息来计算物体表面的深度信息。
投影仪和相机的相对位置和参数需要进行标定,以便准确地获取三维形状信息。通过计算相机图像中每个像素对应的相位差,可以推导出每个像素点在三维空间中的坐标,从而获得目标物体的三维形状。
相位差计算:
在Fringe-Projection环形投影技术中,相机捕获的图像包含了环形光条在目标物体表面上的形变信息。这些形变信息可以通过计算像素点的相位差来得到。
设环形光条的波长为λ,投影到物体表面的光条对应的相位为φ(x, y),则像素点(x, y)处的相位差Δφ(x, y)可以通过以下公式计算:
Δφ(x, y) = φ(x, y) mod 2π
其中,mod表示取模运算。通常情况下,相位差的范围在[0, 2π]之间。
相位展开:
由于相位差Δφ(x, y)的范围在[0, 2π]之间,当物体表面的形状发生高度变化时,相位差可能会发生突变,导致相位计算的不连续性。为了解决这个问题,需要对相位进行展开处理。
相位展开的目标是找到一个合适的整数k(x, y),使得展开后的相位Unwrapped_Δφ(x, y)满足以下条件:
Unwrapped_Δφ(x, y) = Δφ(x, y) + 2π * k(x, y)
展开后的相位Unwrapped_Δφ(x, y)是连续的,可以更准确地表示物体表面的高度信息。
2、实现过程:
基于Fringe-Projection环形投影技术的人脸三维形状提取算法主要分为以下步骤:投影和图像捕获、相位计算、相位展开和三维坐标计算。下面将详细介绍每个步骤:
投影和图像捕获:
首先,使用投影仪投射环形光条到目标人脸表面。投影光条会在人脸表面产生形变。然后,通过相机捕获人脸表面的图像,图像中包含了环形光条的形变信息。
相位计算:
根据相机捕获的图像,计算每个像素点的相位差Δφ(x, y)。这个步骤需要对图像进行预处理,例如去噪、边缘检测和相位提取等。
相位展开:
对相位差Δφ(x, y)进行展开处理,找到合适的整数k(x, y),得到展开后的相位Unwrapped_Δφ(x, y)。展开的过程可以采用基于像素点相邻性的算法,例如四连通或八连通算法。
三维坐标计算:
根据展开后的相位Unwrapped_Δφ(x, y)和已知的相机投影参数,计算每个像素点在三维空间中的坐标。这个过程需要进行相机标定和坐标转换,得到最终的人脸三维形状信息。
3、应用领域:
基于Fringe-Projection环形投影技术的人脸三维形状提取算法在计算机视觉和人工智能领域有着广泛的应用。其中一些典型的应用包括:
人脸识别和认证:通过获取人脸的三维形状信息,可以提高人脸识别和认证系统的准确性和安全性。
人脸表情分析:人脸的三维形状信息可以用于表情分析和情感识别,帮助理解人脸表情背后的情感状态。
视觉效果和增强现实:人脸的三维形状信息可以应用于视觉效果和增强现实技术,为用户提供更加真实和沉浸式的体验。
医学和生物识别:在医学领域,人脸的三维形状信息可以用于面部重建和面部手术模拟。在生物识别领域,它可以用于年龄估计和性别识别等应用。
基于Fringe-Projection环形投影技术的人脸三维形状提取算法是一种非接触式的三维扫描方法,通过投影和相机捕获来获取人脸的深度信息。该算法的实现过程包括投影和图像捕获、相位计算、相位展开和三维坐标计算。它在人脸识别、表情分析、视觉效果、医学和生物识别等领域有着广泛的应用前景。然而,在实际应用中,还需要考虑算法的精度、速度和适用场景等因素,以满足不同应用场景的需求。
4.部分核心程序
figure;
imshow(Images);
title('原图');
%显示原始图像
% 变量 bw 设置为 12,作为 face2 图像的标志
bw = 10;
%傅里叶域处理
Images_fft = fftshift(fft2(Images));% 对图像进行傅里叶变换,并将零频率移到图像中心
figure;
subplot(131);
imagesc(log(abs(Images_fft)));
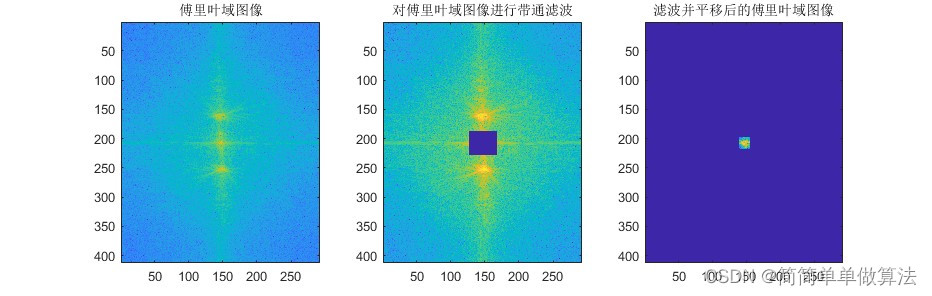
title('傅里叶域图像');% 显示傅里叶域图像
bandf = zeros(size(Images_fft)); % 创建与傅里叶域图像大小相同的全零矩阵 bandf
% 找到傅里叶域图像中的最大值对应的坐标
[cent_x,cent_y] = find(abs(Images_fft)==max(max(abs(Images_fft))));
% 设置中心点附近的频率分量为零,以去除低频信息
Images_fft(cent_x-20:cent_x+20,cent_y-20:cent_y+20) = 0;
subplot(132);
imagesc(log(abs(Images_fft)));
title('对傅里叶域图像进行带通滤波');% 显示傅里叶域图像
% 对傅里叶域图像进行带通滤波,保留高频信息
Images_fft_bp=Images_fft.*bandf;
% 对滤波后的傅里叶域图像进行平移,使零频率恢复到图像中心
shift_x = cent_x - side_max_x;
shift_y = cent_y - side_max_y;
Images_fft_bp = circshift(Images_fft_bp,[shift_x shift_y]);
subplot(133);
imagesc(log(abs(Images_fft_bp)));
title('滤波并平移后的傅里叶域图像');


 浙公网安备 33010602011771号
浙公网安备 33010602011771号