基于LeNet网络的MNIST手写数字训练和识别matlab仿真
1.算法理论概述
基于LeNet网络的MNIST手写数字训练和识别的实现步骤。首先,我们将介绍MNIST数据集的基本信息和LeNet网络的结构及其原理。然后,我们将详细说明数据预处理、LeNet网络的实现过程和训练过程。最后,我们将展示如何使用训练好的LeNet网络对手写数字进行识别,并对实验结果进行分析和总结。
1.1、MNIST数据集和LeNet网络
MNIST数据集是一组手写数字图像数据集,包含训练集和测试集。训练集包含60,000个图像,测试集包含10,000个图像。每个图像都是28x28像素的灰度图像,标注数字为0-9。MNIST数据集被广泛应用于机器学习领域,特别是图像识别领域。LeNet网络是一种经典的卷积神经网络,由Yann LeCun等人于1998年提出。它是第一个成功应用于手写数字识别的深度学习模型,并为后来的深度学习模型奠定了基础。LeNet网络包含两个卷积层和三个全连接层,采用Sigmoid激活函数和平均池化操作。
1.2、数据预处理
在使用MNIST数据集进行训练之前,我们需要对数据进行预处理。首先,我们将每个像素的灰度值从0-255归一化为0-1之间的实数。其次,我们将每个图像展开为一个784维的向量,并将其作为网络的输入。读取MNIST数据集,并将其划分为训练集和测试集。将训练集和测试集中的每个像素的灰度值从0-255归一化为0-1之间的实数。是将训练集和测试集中的每个图像展开为一个784维的向量,并将其作为网络的输入。
1.3、LeNet网络的实现
在数据预处理完成后,我们可以开始实现LeNet网络。
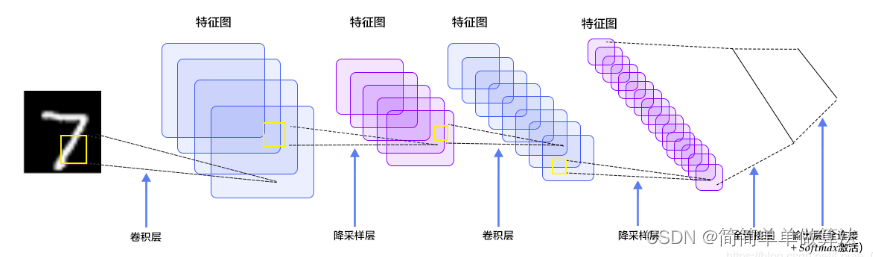
具体的实现过程如下:
初始化网络参数。包括卷积核、偏置项和全连接层的权重和偏置项。
对输入图像进行卷积和Sigmoid激活操作,得到第一个卷积层的特征映射。
对第一个卷积层的特征映射进行平均池化操作,得到第一个池化层的特征映射。
对第一个池化层的特征映射进行卷积和Sigmoid激活操作,得到第二个卷积层的特征映射。
对第二个卷积层的特征映射进行平均池化操作,得到第二个池化层的特征映射。
将第二个池化层的特征映射展开为一个向量,并输入到三个全连接层中,并进行Sigmoid激活操作。
具体的LeNet网络实现过程如下:
初始化网络参数
LeNet网络的初始化包括初始化卷积核和偏置项以及全连接层的权重和偏置项。我们可以使用随机初始化的方法来初始化这些参数,例如从均匀分布或高斯分布中随机抽取参数。
卷积和Sigmoid激活操作

其中,$h^{(p)}{i,j,k}$表示第$p$个池化层的第$k$个特征映射中第$(i,j)$个像素的值,$h^{(p-1)}{i,j,k}$表示第$p-1$个池化层的第$k$个特征映射中第$(i,j)$个像素的值,$p$表示池化窗口的大小。对于LeNet网络的三个全连接层,我们将池化层的输出展开为一维向量,并将其输入到全连接层中:
$$ h^{(fc)}{i} = \sigma(\sum{j=1}^{120} w^{(fc)}{i,j}h^{(4)}{j}
继续
b^{(fc)}_i) $$
其中,$h^{(fc)}{i}$表示第$i$个全连接层的输出,$w^{(fc)}{i,j}$表示第$i$个全连接层的第$j$个神经元的权重,$h^{(4)}_{j}$表示第四个池化层的第$j$个特征映射的值,$b^{(fc)}_i$表示第$i$个全连接层的偏置项。

其中,$w_{i,j}$表示网络中的一个参数,$\alpha$表示学习率,$L$表示损失函数。
我们可以通过多次迭代以上三个步骤,不断优化网络的参数,使得网络的识别准确度不断提高。
1.5、手写数字识别
在完成网络的训练后,我们可以使用训练好的网络对手写数字进行识别。具体的识别过程如下:
读取一张手写数字的图像,并进行预处理。即将图像resize为28x28大小,并将像素值归一化到0-1之间。
将预处理后的图像输入到训练好的LeNet网络中,得到网络的输出结果。
对网络的输出结果进行解码,得到手写数字的识别结果。
具体地,我们找到输出向量中概率值最大的元素的下标,即为识别结果。
2.算法运行软件版本
matlab2022a
3.算法运行效果图预览

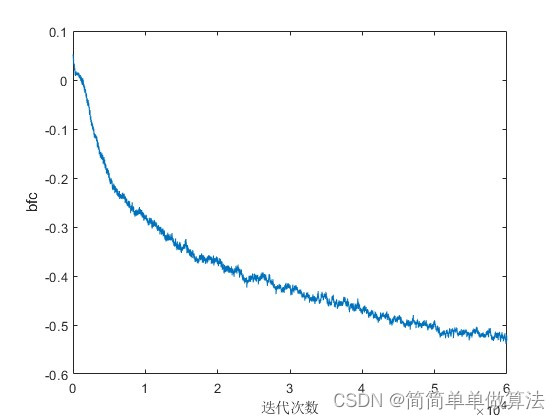
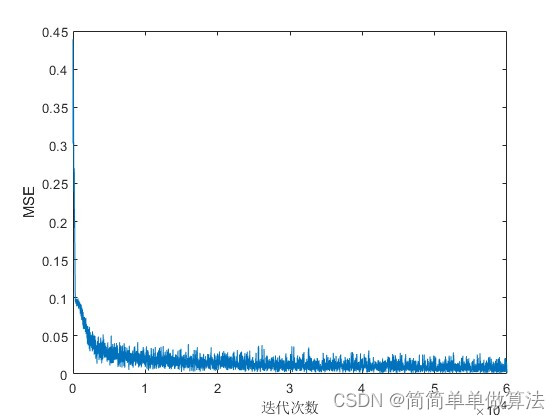
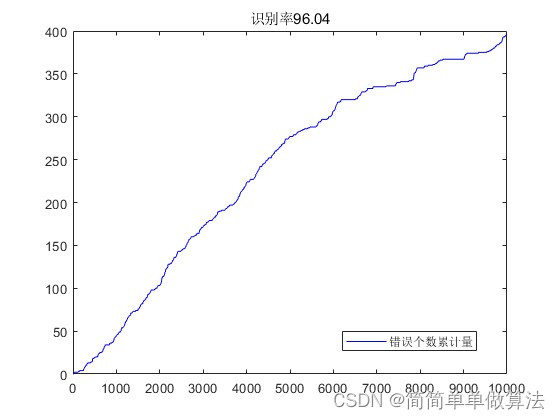
4.部分核心程序
% 通过第二个子采样层反向传播梯度
dE_dH4 = cell(1,12);
dE_dH5 = cell(1,12);
% 将梯度向量转换成矩阵形式
for f=1:12
dE_dH5{f} = reshape(dE_dX{f},4,4);
dE_dH4{f} = zeros(8,8);
for i=1:4
for j=1:4
% 用 0.25 的权重分配到上一层的梯度矩阵中
dE_dH4{f}(i*2-1:i*2,j*2-1:j*2) = dE_dH5{f}(i,j)*0.25;
end
end
end
% 计算第三卷积层权重和偏置的梯度
dH4_dW3 = cell(1,12);
dH4_dB3 = cell(1,12);
for f = 1:12
% 计算第三卷积层的权重和偏置梯度
[dH4_dW3{f},dH4_dB3{f}] = func_grad(H{3}{f},H{4}{f},w);
end
% 根据第三卷积层权重和偏置的梯度计算第三卷积层误差的权重和偏置梯度
dE_dW3 = cell(1,12);
dE_dB3 = cell(1,12);
for f=1:12
% 初始化误差梯度矩阵
dE_dW3{f} = zeros(w);
% 遍历第三卷积层输出的每个位置
for i=1:8
for j=1:8
% 根据链式法则计算误差梯度矩阵
dE_dW3{f} = dE_dW3{f} + dE_dH4{f}(i,j).*dH4_dW3{f}{i,j};
end
end
% 计算第三卷积层误差的偏置梯度
dE_dB3{f} = dE_dH4{f}.*dH4_dB3{f};
end
% 计算反向传播到第一卷积层的梯度
dH4_dH3 = cell(1,12);
for f=1:12
% 根据第三卷积层的权重计算反向传播到第一卷积层的梯度
dH4_dH3{f} = func_gradw(H{3}{f},H{4}{f},Ws{3}{f});
end
% 根据反向传播到第三卷积层的梯度计算反向传播到第一卷积层的梯度
dE_dH3 = cell(1,12);
for f=1:12
dE_dH3{f} = zeros(size(H{3}{f}));
% 遍历第三卷积层输出的每个位置
for i=1:8
for j=1:8
% 根据链式法则计算反向传播到第一卷积层的梯度
dE_dH3{f} = dE_dH3{f} + dE_dH4{f}(i,j).*dH4_dH3{f}{i,j};
end
end
end



 浙公网安备 33010602011771号
浙公网安备 33010602011771号