在matlab中使用模糊编辑器实现模糊控制器的设计详解
目录
一、理论基础
所谓模糊控制技术是指通过模糊集合和模糊逻辑等原理,并且和经典的控制理论相结合,并通过模拟人类的思考方式,对一些难以建模的控制对象进行控制的一种控制策略。模糊控制器的模糊规则的制定是建立在专家经验的基础之上的,即通过具有丰富经验的专家对控制对象进行分析,并基于个人经验建立一套合理的控制机制,通过参数化的方式将这些经验用具体的数学参数和公式进行建模,从而得到一个符合实际情况的控制。这种控制策略通过使用专家经验知识,将专家的经验转换为控制方式,对过程复杂、模型不精确的控制系统进行有效的控制。这种将个人的经验转换为具体的数学公式,并通过模糊数学理论将其转换为模糊控制的过程,就是模糊控制理论。通常情况下,模糊控制器的基本结构如图所示。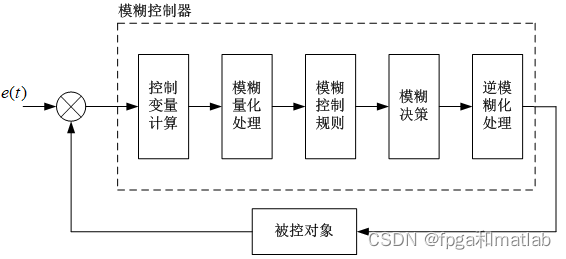
从图的模糊控制器的基本结构图可知,模糊控制器的核心部分包括控制变量计算,模糊量化处理,模糊控制规则,模糊决策以及逆模糊化处理五个模块。整个控制系统通过计算机编程来实现的,将模糊控制器的反馈输出信号和参考输入信号的误差作为整个模糊控制器的输入控制信号,将误差信号转换为模糊量,并通过模糊语言来表示,从而得到的模糊语言集合的一个子集e,然后由子集e和模糊控制规则R,然后根据模糊推理的合成规则进行模糊决策,得到模糊控制量u,u的关系。
一个标准的模糊控制系统和传统的控制方法想比较有如下几个优点:首先,模糊控制器具有较为广泛的应用范围,这种特性比较适合应用在非线性系统中;其次,模糊控制器的控制过程独立于控制对象,且对于一些较为复杂的难以建模的控制对象,可以通过模糊控制器进行有效的控制。模糊控制器具有较好的鲁棒性,对被控对象的特征变化不敏感,而且模糊控制器的设计参数可随时根据需要进行调整。模糊控制以计算机为主,模糊控制的数学计算都由计算机来完成,得到的结果精确,表现出很强的智能性,操作简单易实现。
模糊控制器中的模糊控制规则表格的制定是通过模糊条件语句来设计的,所以模糊控制器本质上也是一种模糊语言控制器,即一个标准的模糊化控制器包括模糊接口、知识库和推理以及解模糊接口。
对于一个模糊输入变量,模糊子集通的划分主要三种类型:
五个模糊集合的控制变量,即负大(Negative big,NB),负小(Negative small,NS),零(Zero,ZO),正小(Positive small,PS),正大(Positive big,PB);
六个模糊集合的控制变量,即负大(Negative big,NB),负中(Negative middle,NM),负小(Negative small,NS),零(Zero,ZO),正小(Positive small,PS),正中(Positive middle,PM),正大(Positive big,PB);
七个模糊集合的控制变量,即负大(Negative big,NB),负中(Negative middle,NM),负小(Negative small,NS),零负(Negative Zero,NZ),零正(Positive Zero,NZ),正小(Positive small,PS),正中(Positive middle,PM),正大(Positive big,PB)。
根据控制器控制精度的不同需求,选择不同划分精度的模糊输入变量。
首先对于模糊控制库,其结构上由一个规则库和一个数据库两个部分构成。其中规则库中保存的是模糊规则,模糊规则是一种基于专家经验知识,并根据某种推理获得的模糊语言表现;而数据库中保存的是输入、输出的模糊子集的隶属函数值。
其次对于模糊控制器的推理过程,其主要通过模糊控制器所输入的模糊变量,通过模糊规则来实现模糊推理来获得模糊控制输出量。此输出量是一种模糊矢量信号,需要通过模糊清晰化处理获得精确的控制输出作为最终的控制量,即解模糊过程。
在一个完整的模糊控制系统中,通过根据输入控制器的个数,将模糊控制器划分为一维模糊控制器,二维模糊控制器以及多维模糊控制器,即通过模糊控制器的输入个数定位模糊控制器的维度,图2所示的是不同输入格式的模糊控制器结构图.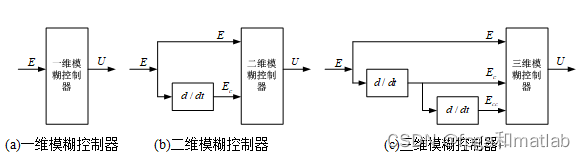
模糊控制器的语言等级,从负最大到正最大依次为:NB负大、NM负中、NS负小、ZO零、PS正小、PM正中、PB正大。选取模糊语言输入变量E、Ec和输出变量、的模糊值域分别为{NB,NM,NS,ZO,PS,PM,PB}。
在MATLAB中,使用模糊函数编辑工具设计上述讲述的模糊模糊集和隶属函数。 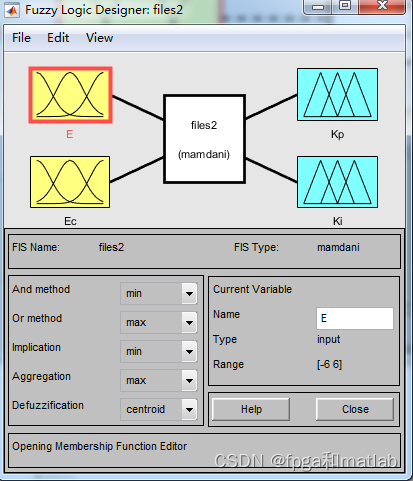

在图的模糊控制器工具箱设计界面,根据模糊隶属函数的选择原则,系统中的NB和PB采用正态型分布;NM、NS、20、Ps、PM则采用三角形分布,模糊控制器输入输出参数的隶属度函数图。
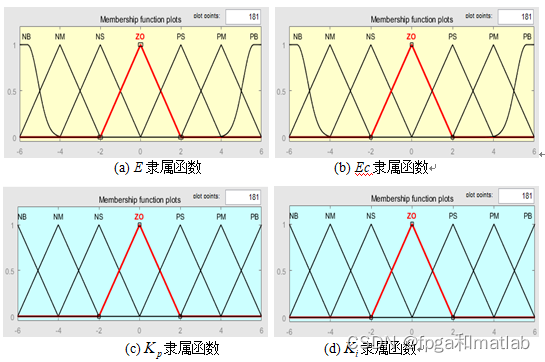
图4 模糊控制器输入输出参数隶属度函数
通过上面的设置,可以获得如下结构的模糊控制器:
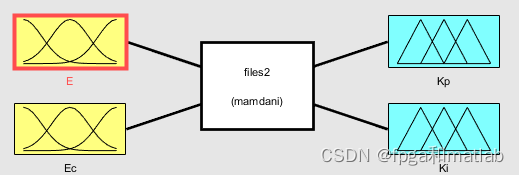
根据模糊规则的性质,并由模糊语言的等级可以得知,模糊控制规则有49条模糊条件语句。故本文所建立的模糊规则表如下所示。
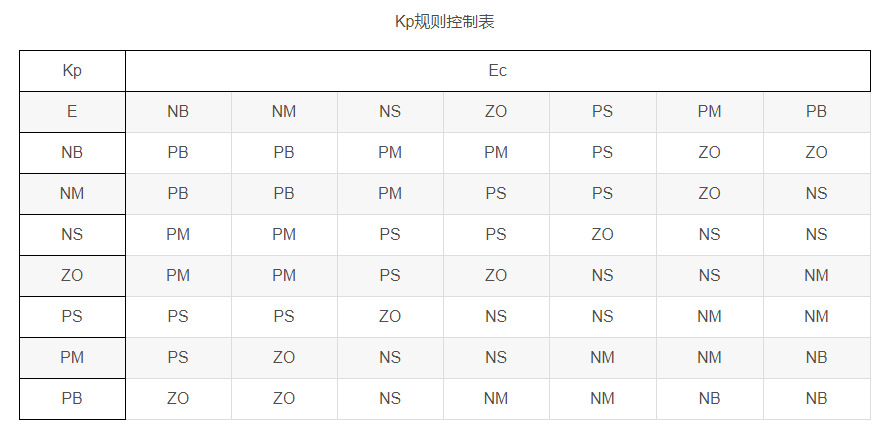
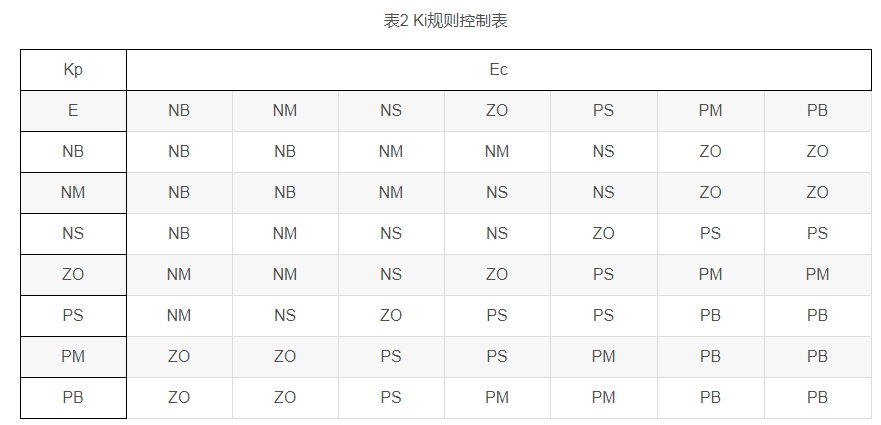
上述模糊规则,其相应的判决条件如下所示:
if (E is NB) and (Ec is NB) then (Kp is PB) and (Ki is NB)
if (E is NM) and (Ec is NB) then (Kp is PB) and (Ki is NB)
if (E is NS) and (Ec is NB) then (Kp is PM) and (Ki is NB)
if (E is ZO) and (Ec is NB) then (Kp is PM) and (Ki is NM)
if (E is PS) and (Ec is NB) then (Kp is PS) and (Ki is NM)
if (E is PM) and (Ec is NB) then (Kp is PS) and (Ki is ZO)
if (E is PB) and (Ec is NB) then (Kp is ZO) and (Ki is ZO)
if (E is NB) and (Ec is NM) then (Kp is PB) and (Ki is NB)
if (E is NM) and (Ec is NM) then (Kp is PB) and (Ki is NB)
if (E is NS) and (Ec is NM) then (Kp is PM) and (Ki is NM)
if (E is ZO) and (Ec is NM) then (Kp is PM) and (Ki is NM)
if (E is PS) and (Ec is NM) then (Kp is PS) and (Ki is NS)
if (E is PM) and (Ec is NM) then (Kp is ZO) and (Ki is ZO)
if (E is PB) and (Ec is NM) then (Kp is ZO) and (Ki is ZO)
反模糊化处理运算主要是根据模糊推理模块所产生的模糊集求出控制器的输出。目前为止,较为常用的反模糊化处理算法有最大隶属度法、加权平均法、隶属度限幅元素平均法以及重心法等。本文将使用重心法来进行反模糊化处理运算,该方法通过选择模糊隶属函数曲线与横坐标围成面积的重心为代表点输出,其数学计算公式为: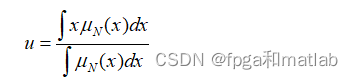
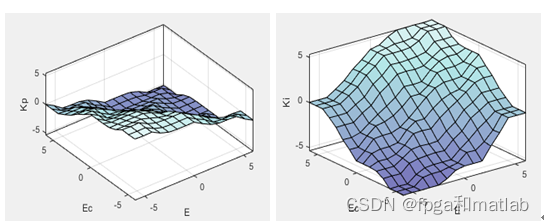
最后,对于一个二维输入的模糊控制器,通过一个三维坐标图绘制出模糊控制的输出与输入之间的关系。该三维坐标图的纵坐标表示模糊控制器输出控制量的曲面。曲面用简洁的形式表现出模糊控制器的所有信息,采用MATLAB模糊控制工具箱绘制本文所设计的模糊控制器的控制面如图所示。
二、核心程序
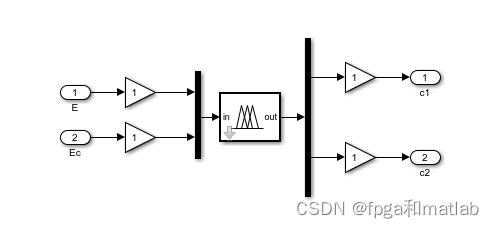
我们的模糊规则fis文件如下:
[System]
Name='files2'
Type='mamdani'
Version=2.0
NumInputs=2
NumOutputs=2
NumRules=49
AndMethod='min'
OrMethod='max'
ImpMethod='min'
AggMethod='max'
DefuzzMethod='centroid'
[Input1]
Name='E'
Range=[-6 6]
NumMFs=7
MF1='NB':'gauss2mf',[0.5182 -6.39 0.5182 -5.61]
MF2='NM':'trimf',[-6 -4 -2]
MF3='NS':'trimf',[-4 -2 0]
MF4='ZO':'trimf',[-2 0 2]
MF5='PS':'trimf',[0 2 4]
MF6='PM':'trimf',[2 4 6]
MF7='PB':'gauss2mf',[0.5182 5.61 0.5182 6.39]
[Input2]
Name='Ec'
Range=[-6 6]
NumMFs=7
MF1='NB':'gauss2mf',[0.5182 -6.39 0.5182 -5.61]
MF2='NM':'trimf',[-6 -4 -2]
MF3='NS':'trimf',[-4 -2 0]
MF4='ZO':'trimf',[-2 0 2]
MF5='PS':'trimf',[0 2 4]
MF6='PM':'trimf',[2 4 6]
MF7='PB':'gauss2mf',[0.5182 5.61 0.5182 6.39]
[Output1]
Name='Kp'
Range=[-6 6]
NumMFs=7
MF1='NB':'trimf',[-8 -6 -4]
MF2='NM':'trimf',[-6 -4 -2]
MF3='NS':'trimf',[-4 -2 0]
MF4='ZO':'trimf',[-2 0 2]
MF5='PS':'trimf',[0 2 4]
MF6='PM':'trimf',[2 4 6]
MF7='PB':'trimf',[4 6 8]
[Output2]
Name='Ki'
Range=[-6 6]
NumMFs=7
MF1='NB':'trimf',[-8 -6 -4]
MF2='NM':'trimf',[-6 -4 -2]
MF3='NS':'trimf',[-4 -2 1.776e-015]
MF4='ZO':'trimf',[-2 0 2]
MF5='PS':'trimf',[1.776e-015 2 4]
MF6='PM':'trimf',[2 4 6]
MF7='PB':'trimf',[4 6 8]
[Rules]
1 1, 7 1 (1) : 1
2 1, 7 1 (1) : 1
3 1, 6 1 (1) : 1
4 1, 6 2 (1) : 1
5 1, 5 2 (1) : 1
6 1, 5 4 (1) : 1
7 1, 4 4 (1) : 1
1 2, 7 1 (1) : 1
2 2, 7 1 (1) : 1
3 2, 6 2 (1) : 1
4 2, 6 2 (1) : 1
5 2, 5 3 (1) : 1
6 2, 4 4 (1) : 1
7 2, 4 4 (1) : 1
1 3, 6 2 (1) : 1
2 3, 6 2 (1) : 1
3 3, 6 3 (1) : 1
4 3, 5 3 (1) : 1
5 3, 4 4 (1) : 1
6 3, 3 5 (1) : 1
7 3, 2 5 (1) : 1
1 4, 6 2 (1) : 1
2 4, 5 3 (1) : 1
3 4, 5 3 (1) : 1
4 4, 4 4 (1) : 1
5 4, 3 5 (1) : 1
6 4, 2 5 (1) : 1
7 4, 2 6 (1) : 1
1 5, 5 3 (1) : 1
2 5, 5 3 (1) : 1
3 5, 4 4 (1) : 1
4 5, 3 5 (1) : 1
5 5, 3 5 (1) : 1
6 5, 2 6 (1) : 1
7 5, 2 6 (1) : 1
1 6, 4 4 (1) : 1
2 6, 4 4 (1) : 1
3 6, 3 5 (1) : 1
4 6, 2 6 (1) : 1
5 6, 2 6 (1) : 1
6 6, 2 7 (1) : 1
7 6, 1 7 (1) : 1
1 7, 4 4 (1) : 1
2 7, 3 4 (1) : 1
3 7, 3 5 (1) : 1
4 7, 2 6 (1) : 1
5 7, 2 7 (1) : 1
6 7, 1 7 (1) : 1
7 7, 1 7 (1) : 1
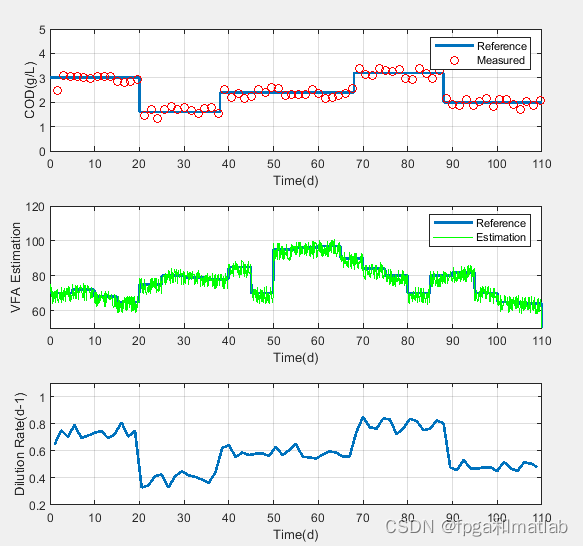
三、测试结果
08-54


 浙公网安备 33010602011771号
浙公网安备 33010602011771号