MT【250】距离0-7

是否存在一个正方体,它的8个顶点到某一个平面的距离恰好为$0,1,2,3,4,5,6,7$ ?若存在指出正方体与相应的平面的位置关系.不存在说明理由.

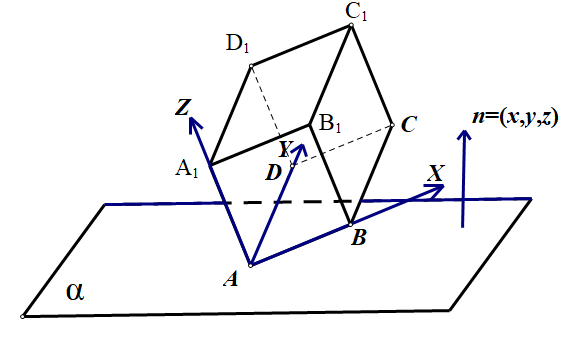
分析:设平面$\alpha$的单位法向量为$\overrightarrow{n}=(x,y,z),\textbf{其中}x^2+y^2+z^2=1$.

如图以A为原点,$AB,AD,AA_1$分别为$x,y,z$轴建系.设正方体边长为 $t$ 由题意并考虑各面中心重合得

$$\begin{cases} \overrightarrow{AB}\cdot\overrightarrow{n}=&1\\ \overrightarrow{AD}\cdot\overrightarrow{n}=&2\\ \overrightarrow{AA_1}\cdot\overrightarrow{n}=&4\\ \end{cases}$$
得 $tx=1,ty=2,tz=4$ 故 $t=\sqrt{21}$
又
$$\begin{cases} \overrightarrow{AC}\cdot\overrightarrow{n}=&3\\ \overrightarrow{AC_1}\cdot\overrightarrow{n}=&7\\ \overrightarrow{AB_1}\cdot\overrightarrow{n}=&5\\ \overrightarrow{AD_1}\cdot\overrightarrow{n}=&6\\ \end{cases}$$
得 $t(x+y)=3,t(z+x)=5,t(y+z)=6,t(x+y+z)=7$
得 $x=\dfrac{1}{\sqrt{21}},y=\dfrac{2}{\sqrt{21}},z=\dfrac{4}{\sqrt{21}}$