MT【193】三面角的正余弦定理

(原题为浙江名校新高考研究联盟2018届第三次联考选择压轴题)

在平面$\alpha$内，已知$AB\perp BC$,过直线$AB,BC$分别作平面$\beta,\gamma$，使得锐二面角$\alpha-AB-\beta$为$\dfrac{\pi}{3}$，锐二面角$\alpha-BC-\gamma$为$\dfrac{\pi}{3}$，则平面$\beta$和平面$\gamma$所成的锐二面角的余弦值为____

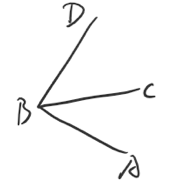
提示:如图注意到以下结论：(三面角的第二余弦定理)$\cos D=-\cos A\cos C+\sin A\sin C\cos \angle CBA$

其中$A,C,D$分别表示二面角$D-BA-C,D-BC-A,A-BD-C$所表示的二面角的平面角

此题中$\alpha-AB-\beta=C-AB-D；\alpha-BC-\gamma=A-BC-D$代入数值得$\cos D=-\cos\dfrac{\pi}{3}\cos\dfrac{\pi}{3}=-\dfrac{1}{4}$

由于所求为锐二面角，故答案为$\dfrac{1}{4}$.

 

 

注:

1.三面角的正弦定理如图为:$\dfrac{\sin D}{\sin\angle CBA}=\dfrac{\sin C}{\sin\angle DBA}=\dfrac{\sin A}{\sin\angle CBD}$ 

2.三面角的第一余弦定理(三射线定理):$\cos\angle CBA=\cos\angle DBA\cos\angle DBC+\sin\angle DBA\sin\angle DBC\cos D$

3.与这些类似的还有一个和线面角最小有关的三余弦定理.