MT【32】内外圆(Apollonius Circle)的几何证明
另一方面,如果 M 满足(1)式,那么M必然在以PQ为直径的圆上.事实上当M为P或者Q时,这是显然的。当M异于P,Q时,由$\frac{|MB|}{|MC|}=\frac{|PB|}{|PC|}=\lambda,\frac{|MB|}{|MC|}=\frac{|QB|}{|QC|}=\lambda$知MP,MQ分别是$\angle{BMC}$的内角平分线和外交平分线,故$\angle{PMQ}=90^0$,即M在以PQ为直径的圆上。
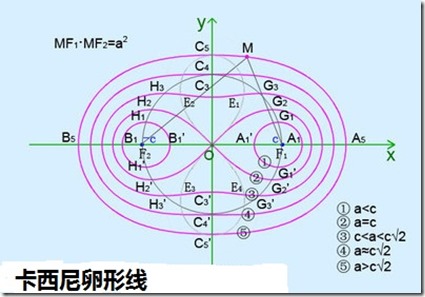
评:阿式圆因为涉及到内角平分线和外角平分线又称为内外圆,在有些高考题中非常的管用.这个圆的定义大家可以和高中教材中椭圆双曲线的定义做比较,自然会想到以下问题:到两个定点的乘积为定值的点的轨迹是什么?
注:卡西尼卵形线图像:
解答:
懂,会,熟,巧;趁青春尚在,奋力前行,追求卓越!








 浙公网安备 33010602011771号
浙公网安备 33010602011771号