MT【349】同时取到

已知$\theta \in[0,2\pi]$求$2\cos\theta-\sin\theta-\dfrac{\sin\theta+\sqrt{5}}{\cos\theta+\sqrt{5}}$的最小值_____
分析:$2\cos\theta-\sin\theta-\dfrac{\sin\theta+\sqrt{5}}{\cos\theta+\sqrt{5}}=\textbf{ON}\cdot \textbf{OP}+k_{PM}\ge-\sqrt{5}-2$

当$P(-\dfrac{2}{\sqrt{5}},\dfrac{1}{\sqrt{5}})$时取到最小值.

如图$M(-\sqrt{5},-\sqrt{5})，N(2,-1)$

 

注：最大值可以用万能公式变形为

$2\cos\theta-\sin\theta-\dfrac{\sin\theta+\sqrt{5}}{\cos\theta+\sqrt{5}}=\dfrac{2-2t^2-2t}{1+t^2}-\dfrac{\sqrt{5}t^2+2t+\sqrt{5}}{(\sqrt{5}-1)t^2+1+\sqrt{5}}$

其中$t=\tan\dfrac{\theta}{2}\in R$求导可知

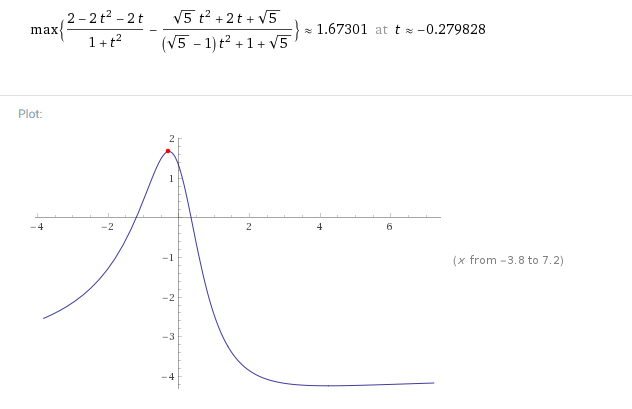
最小值几何意义明显，适合做考题.最大值不适合做考题