MT【340】彭塞列闭合定理

如图,设点$P$时抛物线$C_1:y^2=4x$上的动点,过$P$作圆$C_2:(x-3)^2+y^2=r^2(r>0)$的两条切线交抛物线$C_1$于$A,B$两点,其中$M,N$为切点.若过$A,B$两点的直线恒与$C_2$ 相切,求$r$的值.

 

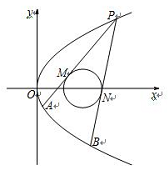
解答:

从必要性入手,当$P(0,0)$时,由几何关系易知半径满足$r^3+7r^2-36=0$
故$r=2,r=-3,r=-6$由题意$r>0$知道$r=2$
下证:$r=2$时,满足要求.设$P(t^2,2t),A(t_1^2,2t_1),B(t_2^2,2t_2)$,则$PA:2x-(t+t_1)y+2tt_1=0$
圆心$(3,0)$到直线$PA$距离$d=\dfrac{|6+2t_1t|}{\sqrt{4+(t_1+t)^2}}=r=2$整理得$(t^2-1)t_1^2+4tt_1+5-t^2=0$
同理$PB$与圆相切得$(t^2-1)t_2^2+4tt_2+5-t^2=0$
故$t_1+t_2=-\dfrac{4t}{t^2-1},t_1*t_2=\dfrac{5-t^2}{t^2-1}$
此时$AB:2x-(t_1+t_2)y+2t_1t_2=0$
圆心$(3,0)$到直线$AB$的距离$d=\dfrac{|6+2t_1t_2|}{\sqrt{4+(t_1+t_2)^2}}=\dfrac{|6+2*\frac{5-t^2}{t^2-1}|}{\sqrt{4+(-\frac{4t}{t^2-1})^2}}=2=r$
故此时$AB$与圆也相切.

注:如果是填空事实上由彭赛列闭合定理知道只需考察特殊点$P(0,0)$

注:抛物线换成椭圆可以用巧妙的曲线系方程得到其它解法，但抛物线貌似行不通.

注:此题类似的有2011浙江省高考解析几何大题

练习:

 

最后农历生日之际给自己点首歌 《阳光总在风雨后》，但愿这辈子生活中所有的不愉快和不幸都已经过去,接下来的日子祝愿自己和身边的人一切顺利！