MT【294】函数定义的理解
已知函数$f(x)$的定义域为$D,\pi\in D$.若$f(x)$的图像绕坐标原点逆时针旋转$\dfrac{\pi}{3}$后与原图像重合,
则$f(\pi)$不可能是( )
A$\dfrac{\sqrt{3}}{2}\pi$
B$\sqrt{3}\pi$
C$\pi$
D$\sqrt{2}\pi$

提示:可以考虑圆周上间隔为$\dfrac{\pi}{3}$的6个点,若$f(\pi)=\sqrt{3}\pi$,可以发现$x=\pi$时圆周上对应有两个点,与函数定义不符.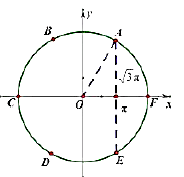
练习:(2018上海高考选择压轴题)
已知函数$f(x)$的定义域为$D,1\in D$.若$f(x)$的图像绕坐标原点逆时针旋转$\dfrac{\pi}{6}$后与原图像重合,
则$f(1)$的可能取值只能是( )
A$\sqrt{3}$
B$\dfrac{\sqrt{3}}{2}$
C$\dfrac{\sqrt{3}}{3}$
D$0$
答案:B
懂,会,熟,巧;趁青春尚在,奋力前行,追求卓越!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号