MT【257】任意存在并存
函数$f(x)=\dfrac{4x}{x+1}(x>0),g(x)=\dfrac{1}{2}(|x-a|-|x-b|),(a<b)$, 若对任意$x_1>0$,存在$x_2\le x_1$,使得$g(x_2)=f(x_1)$,则$2a+b$的最大值为____

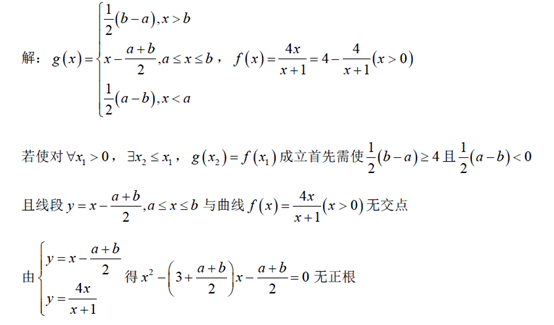
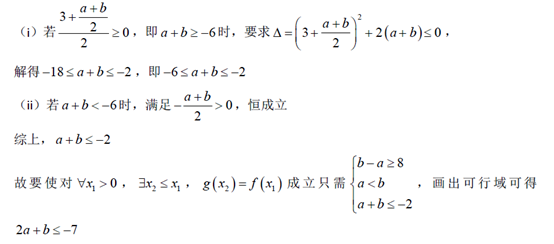
注:由图像知道交点为切点时满足题意.
懂,会,熟,巧;趁青春尚在,奋力前行,追求卓越!
函数$f(x)=\dfrac{4x}{x+1}(x>0),g(x)=\dfrac{1}{2}(|x-a|-|x-b|),(a<b)$, 若对任意$x_1>0$,存在$x_2\le x_1$,使得$g(x_2)=f(x_1)$,则$2a+b$的最大值为____

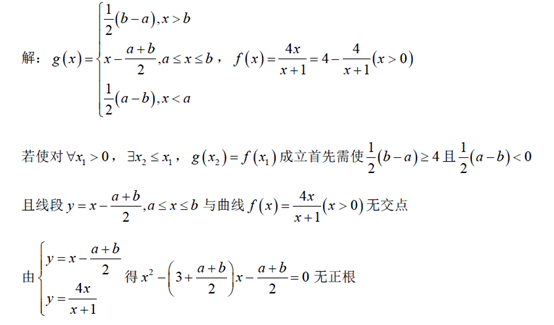
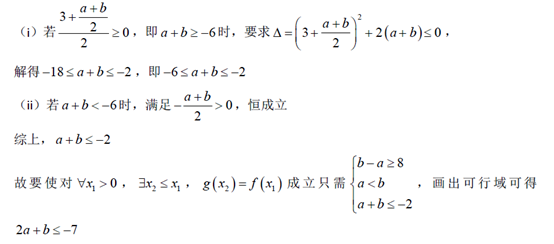
注:由图像知道交点为切点时满足题意.
