MT【255】伸缩变换
(2012新课标9)已知$\omega>0,$函数$f(x)=sin(\omega x+\dfrac{\pi}{4})$在$(\dfrac{\pi}{2},\pi)$上单调递减,则$\omega$的取值范围是______

分析:
常规方法:$\dfrac{\pi}{2}+2k\pi\le\omega x+\dfrac{\pi}{4}\le\dfrac{3\pi}{2}+2k\pi,k\in Z$
得$x\in[\dfrac{\pi+8k\pi}{4\omega},\dfrac{5\pi+8k\pi}{4\omega}]$取$k=0$得$\dfrac{\pi}{4\omega}\le\dfrac{\pi}{2},\dfrac{5\pi}{4\omega}\ge\pi$得$\omega\in[\dfrac{1}{2},\dfrac{5}{4}]$
巧法:利用图像伸缩变换,如图
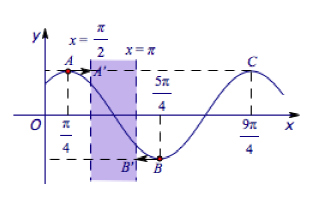
先对函数$f(x)=\sin(x+\dfrac{\pi}{4})$作图,$f(x)=\sin(\omega x+\dfrac{\pi}{4})$是由上图纵坐标不变,横坐标伸缩为原来的$\dfrac{1}{\omega}$所得.
考虑$\dfrac{\pi}{4\omega}=\dfrac{\pi}{2},\dfrac{5\pi}{4\omega}=\pi$易得$\omega\in[\dfrac{1}{2},\dfrac{5}{4}]$
懂,会,熟,巧;趁青春尚在,奋力前行,追求卓越!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号