外文翻译 | 13个有趣的数字—当数学遇上美

13个有趣的数字—当数学遇上美

每个人都有必要知道的数字和数学概念。
https://www.cantorsparadise.com/13-fascinating-numbers-around-us-when-beauty-meets-math-3fa7d3a22126

有时一些特别的数字会被发现于美丽的方程和公式。由这些方程公式的结论所推导出的可视化结论也让他们拥有了数学之美。下面列举出来了从超穷数到黄金比例的13个有趣的数字。

13. 阿列夫零： ℵ0

阿列夫零是一个美丽的概念。它是超穷基数中的最小的数，超穷数就是指无穷大那么大的数。我知道你不相信这个，因为无穷大只是一个概念，不能被用来比较大小，所以超穷数的存在是没有意义的。毕竟如果一个“无穷大”大于另一个“无穷大”，第一个“无穷大”就不应该被叫做无穷大了。

现在假设有一个无穷是什么的基本想法（我们会在之后的第十二条详细讨论）。阿列夫零是指一个自然数的个数那么大的数，这个数需要在数值上足够大并能够很好的符合无穷的特征，因此把像阿列夫零这样的数称为超穷数。

那么如果把自然数输两遍甚至3遍呢？当构建好第一个集合后，我们可以按某种规律拓展自然数集并得到相应的超穷数。让我们为这些数字排个序，或者就按之前得到它们的顺序排列。阿列夫零之后的下一个数是ω，然后是ω+1。后面这两个数是按顺序的但却不够基础，换句话说，它们只是代表了它们在数轴上的前后位置下面的图表是一个更好的简化版的说明。图中每一组可以代表一个自然数集，每一组都包含基础的阿列夫零。再增加1次自然数集并不改变这个构造模式（你可以仅仅改变顺序但你得到的仍然是以阿列夫零为基础的数）。

这有助于讨论它们的顺序。因此，自然数集构造完成后的第一个超穷数是我们前面所讨论的“ω”。

 

 

 

 

A matchstick representation. Source of the image: Wikipedia.

你不会拥有ω个苹果，但你可以花ω的时间完成比赛（如果你真的水平很低的话）。

有趣的是，ω + 1并不一定比ω 大，它只是在ω的后面。这有点难以理解了， 所以只看某几个角度应该有帮助。以下是一些我们所知道的一些概念。

• 无穷和阿列夫零是两样不同的东西。前者是简单依赖于数轴的一个极限的概念，而后者依赖于集合中包含基数个数的多少。
• 基数代表集合的大小而基本的数字代表数量（如1，2，459，1002，...）。另外序数是指集合的次序而按数序排列的数字则代表着序数词（第1，第2，第66，…）
• 事实上存在无穷基数，无穷序数也存在，并且第一个不可数无穷序数就是刚刚讨论过的ω。
• 按照这个逻辑，阿列夫1就是ω的基数。

阿列夫零只是阿列夫大家族中的第一个数。麦可·史蒂文斯创建的YouTube科普频道Vsauce已经制作了一系列有趣的视频讨论这个概念，强烈建议大家去看一看这些视频。

12. 无穷 ：∞

的确，∞更多的是一个想法或概念，而不是一个数字。这个符号通常被称为双扭线。在讨论有关无穷的性质及其他有趣的事情之前，我们要先知道，π也是一种无穷的形式（这个数会在后面文章中细聊），当然我们说的是小数点后面的部分，3.14159…，你很难界定到底第多少位开始才算做第无穷大位，这就是为什么无穷大是一个概念， 而不是我们能够量化的东西。另一个例子来自美丽的分形领域。举个简单的例子，科赫雪花曲线可以被细分为无限多个无限小的相同形状的小段。

 

 

 

 

https://tenor.com/view/koch-fractal-koch-curve-koch-snowflake-infinite-gif-13239066

有趣的是，当把尺度逼近无穷大时，我们想象的内容会变得越来越丰富，但它实际上并没有扩大。它还保持着自身的形状，还是它原来的样子。

再来看看2个与无穷相关的简单的话题（这不需要动什么脑筋，因为我们刚刚聊完阿列夫零，得让我们的大脑进行适当的放松）。有趣的是，虽然在这里我们一帆风顺，集合论之父乔治•康托尔在生命中许多时刻却因为无穷陷入了困境。

0.99999 = 1吗?

很自然地，当0.999…中9的数量趋近于无穷多时，它等于1，从代数上证明这个结论也很容易：

10X = 9.9999

如果分别从两边减去X，就会得到：

9X = 9.9999 -0.9999

9X = 9

再除以9，就有：

X = 1

不可思议吧哈哈哈~

— — —∞ — ∞ = 0吗?

任何数减去它自身都会得到零，但无穷不是一个数，所以不遵循这个原则。下面来做一个测试来验证一下：

∞ — ∞ + 1= 0 + 1 # 两边同时加上1

∞ — ∞ = 1 # 无穷加上1等于无穷，可以利用这个来简化方程

一个意料之外的结果！利用这个方法，可以让无穷减去无穷，来得到任何我们想要的数。因此，用无穷减无穷是没有意义的。

最后，我们还可以知道为什么零不能做除数。 1除以0是没有意义的，然而这并不是一个错误，只是不满足老师讲的故事了。直观的想就是，如果你把一个苹果分给零个人，每个人会得到多少个苹果呢？自然地， 这是一种装不满的无穷。

所以，就有了最开始得到的1 / 0等于∞。那么为什么我们被告知这个结果是没有意义的呢？简单地说，如果用1去除以一个趋近于0的极小的正数时，结果很接近于1/0的结果也就是∞。在这里，∞指代+∞。如果用1去除以一个极其趋近于0的负数时，也算得1 / 0 = -∞。所以到底哪一个才是对的呢？ 到底是 1 / 0 = ∞ 还是 1 / 0 = -∞？这样一来就有了矛盾，我们的答案是有歧义的。这就是为什么不用0作除数的缘故。

以下是一些有关无穷的计算公式：

∞ + ∞ = ∞
-∞ + -∞ = -∞
∞ × ∞ = ∞
-∞ × -∞ = ∞
-∞ × ∞ = -∞

11. 虚数单位：i

字母i的意思是不存在的数，也就是虚数。虚数的定义是，对虚数进行平方运算的时候，会得到一个负数，我们把具有这种特性的数称作虚数。这不是通常意义下的平方运算，因为把某个数乘以它自己时，一般会得到一个正数结果。尽管如此，我们还是不能否认这类数的存在性，这不能成为取消虚数公理的理由。我们称虚数为不存在的数似乎是因为他们不应该存在，那么-6的平方根是多少呢？我们并不知道。计算机会告诉你输入错误因没有实数的平方会是负数。 但是数学之美与其他科学工具不同，你可以假设某个对象存在并调整它们使他们能更好地为你所用。 让我们来尝试使用一下它。

虚数的功能很简单。我们可以预先假设或想象它们存在。那它们有什么用呢？答案之一是可以用它解一些需要用到复数的平方根的方程。让我们来看看具体的例子：

• √4等于多少 ? 很简单, 等于 2.
• √-4等于多少?有点复杂但答案是 2i.

我们添加了代表虚数的i来帮助得到-4的平方根。下面来检验一个通常被称作无解的方程，并看看如何用虚数解决它。

 

 

 

 

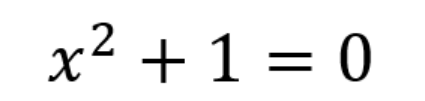
显然，x的平方绝不会得到一个负数（在这里我们用的是-1），所以就假设答案是i（像之前做的那样）。

 

 

 

 

 

 

 

 

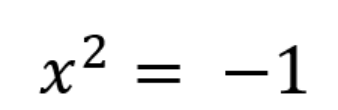
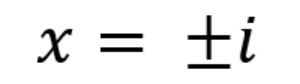
你可以把-1的平方根（也就是√-1）作为虚数单位，就像实数中的1一样。虚数还可以与实数作联合来制作更复杂的数（如7i+12）。不仅如此，在电路设计中，虚数更是常客，要学会使用这个工具。

10.古戈尔数

一古戈尔数等于10的后面缀着100个0，因此，为了描述它，先来看看下面这个数：

 10,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,

或者也可以这样表述它： 

 

 

这个数几乎等于70！（阶乘），70！=70 x 69 x 68 x 67 x 66 x 65 x 64 x 63 x 62 x 61 x 60 x 59 …. x 1。

为了让头脑风暴来的更猛烈，这里还有一个被称作古戈尔丛的数，就是10的古戈尔数次方，它写作：

 

 

 

 

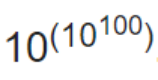
很有意思的是，谷歌公司的名字就是被拼写错误的古戈尔数。不过这确实是命名搜索引擎的好方法。不过这个数更多被用在宇宙大爆炸这样的天文学研究当中。

9.数字 9 (巧合的是这也是我们介绍的第9个数)

可能因为我做贸易的缘故，这是我最喜欢的数字，我觉得它看上去特别美丽，富含数学之美。在几何学中，我们会发现它隐藏在许多地方，例如：

• 整圆. 每个整圆有360° (3 + 6 + 0 = 9)
• 二等分圆.每个半圆有180° (1 + 8 + 0 = 9)
• 四等分圆. 每个四等分圆有90°(9 + 0 = 9)
• 八等分圆. 每个八等分圆有45°(4 + 5 + 0 = 9)
• 16等分圆。每个16等分圆有22.5° (2 + 2 + 5 = 9)
• 32等分圆。每个圆有11.25°(1 + 1 + 2 +5 = 9)
• 圆内接正三角形. 内角和是 60 x 3 (180 = 1 + 8 = 9)
• 正方形. 内角和是 90 x 4 (360 = 3 + 6 + 0 = 9)

接下来是其他圆内接正多边形：

 

 

 

 

 

 

 

 

 

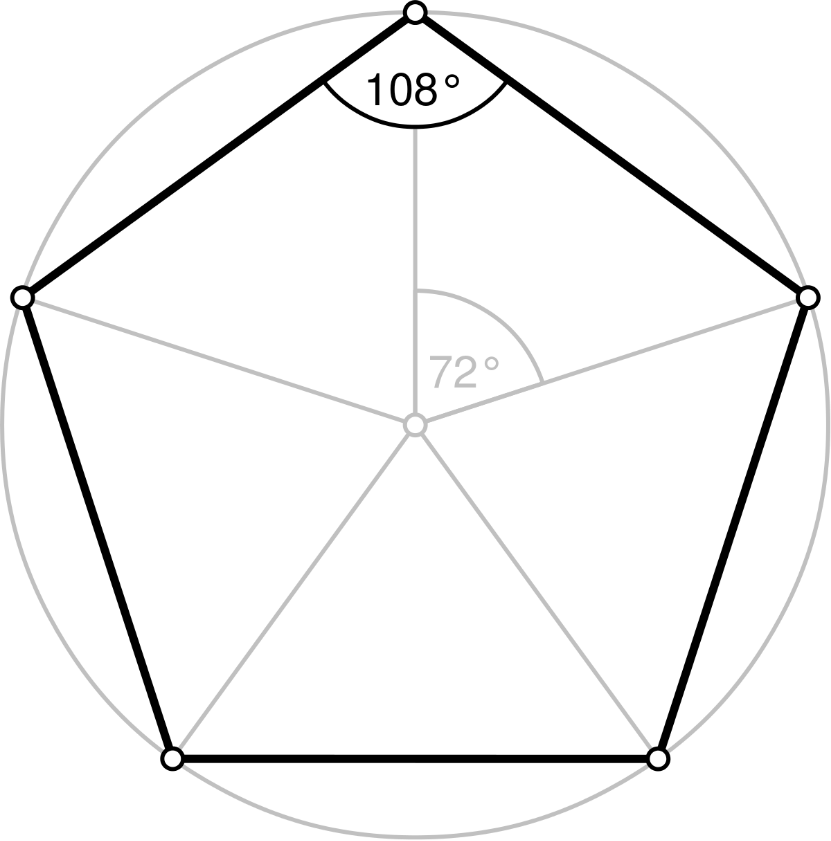
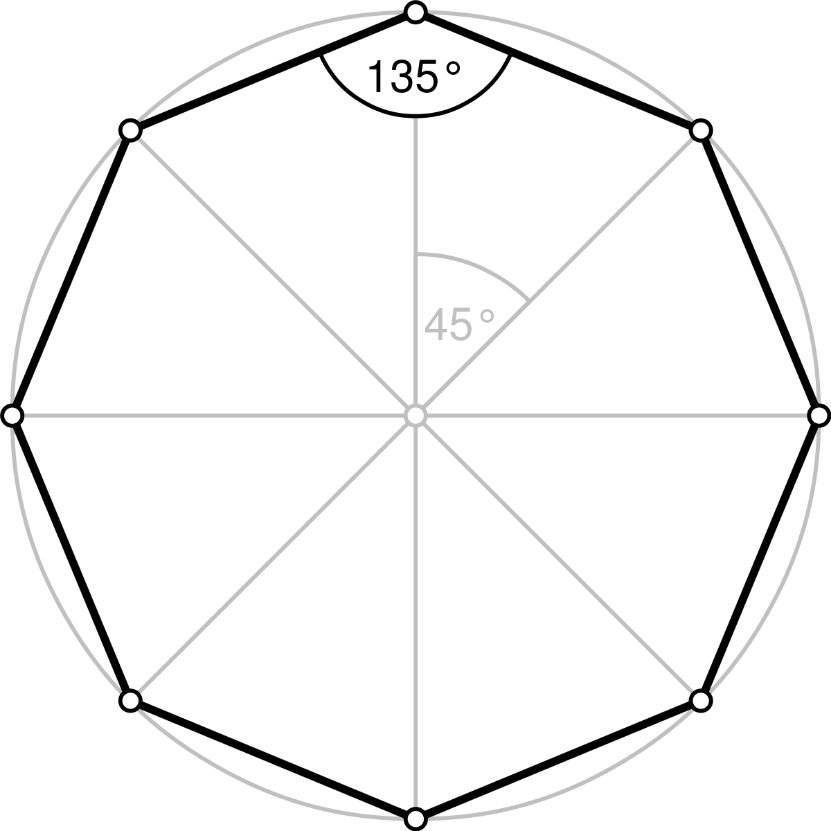
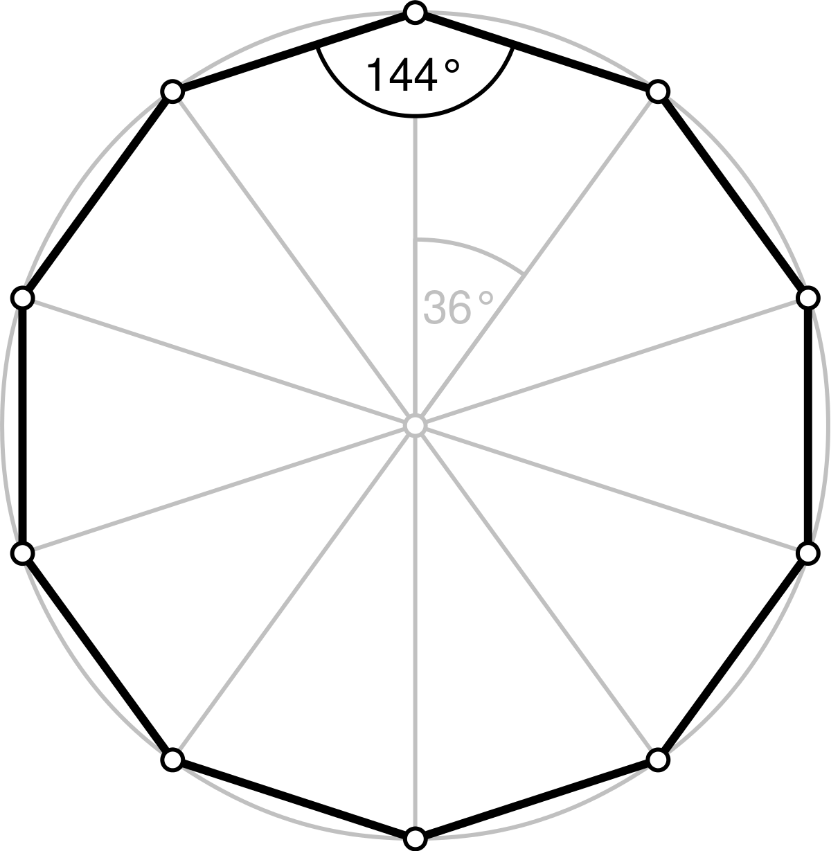
来源： wikipedia.org

从左至右： 五边形, 八边形, 十边形。

• 五边形单角= 108 = 1 + 0 + 8 = 9 // 72 = 7 + 2 = 9
• 八边形单角=135 = 1 + 3 + 5 = 9 // 45 = 4 + 5 = 9
• 十边形单角= 144 = 1 + 4 + 4 = 9 // 36 = 3 + 6 = 9

而且，如果令数字相加，还会回到数字9 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36)。就有3 + 6 = 9

令数字相乘再把每位数上的数字相加也会回到9，例如：

• 9 x 1 = 9
• 9 x 3 = 27 = 2 + 7 = 9
• 9 x 7 = 63 = 6 + 3 = 9
• 9 x 9 = 81 = 8 + 1 = 9

让9除数字也会给出相同数字的无限循环小数，例如：

• 1 / 9 = 0.11111
• 3 / 9 = 0.33333
• 7 / 9 = 0.77777

8. 数字 73

如果你是大数理论迷，你一定听说过谢尔顿古博关于为什么73是完美数的演说，以下是原话：

“73是最好的数字。为什么呢？73是第21个质数，它的镜像37是第12个质数，而12的镜像21则是由指数3乘7产生。

“73的二进制1001001是个回文数，正过来倒过去都是1001001。”

 

这句话取自第十部第四季的节目，巧合的是这是第73集中的台词。（同年，扮演谢尔顿的演员吉姆帕森斯恰好出生）。

7. 欧拉数

被莱纳德•欧拉命名的无理数e是自然对数的底数。有趣的是，欧拉常数e已经被精确到约1万亿位数[来源：mathisfun.com]。而这一切都来自于这个公式：

 

 

 

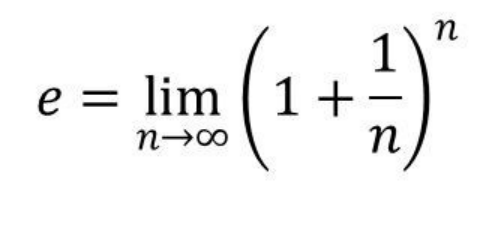
当n趋于无穷大时，会得到一个更精确的e的近似值。当n = 100,000, e = 2.71827。 有个关于e的有趣事实，它的导数是恒定值。另外，e在经济学中也被用于计算复利，相信已经参加终审法院考试的朋友会熟悉这些。

6. 斐波纳契数列

莱昂纳德•波纳契更多被知道为莱纳德•斐波那契（甚至斐波那契还成为了他的一个昵称），他在观察兔子的繁衍时用简单的加法技巧创造了世界上最有趣的数列之一。公平地讲，现在有证据表明有印度数学家在斐波那契之前就知道这个数列，但我们仍然按照主流说法讨论，也就是斐波那契提出了这个数列（不过，了解了有关印度研究者的数学和科学史，我一点儿也不惊讶他们会是最先发现者）。

斐波那契数简单地由满足下面这个简单的方程的n>2的元素构成：

 

 

 

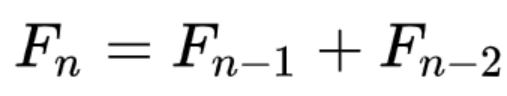
这给出了下面这个趋于无穷大的数列：

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ….

这个数列最美的地方在于它与自然界紧密的联系。举个例子，我们可以在百合开花的过程中看到它的身影，也可以在雏菊花瓣观察到它的踪迹，以及小蜜蜂的筑巢，等等等等…这难道触及到了宇宙中最深处的秘密吗？

盖瑞•梅斯诺发现了一个有趣的结论，这个结论支持地球与月球尺寸之比为Φ，它们形成了一个边之比为1.618的三角形。但什么是Φ，什么又是1.618呢？

如果去看数列中的相邻2个数，当趋近无穷时，它们的比值(Xn / Xn-1)会越来越接近1.618，也就是我们常说的黄金比例： 
3 / 2 = 1.5
13 / 8 = 1.666
55 / 34 = 1.61764
233 / 144 = 1.61805
…
317,811 / 196,418 = 1.61803

当数列越来越趋近于无穷项时比例就会越来越接近1.618，也就是Φ。我们会在后面详细讨论这个数。

 

 

 

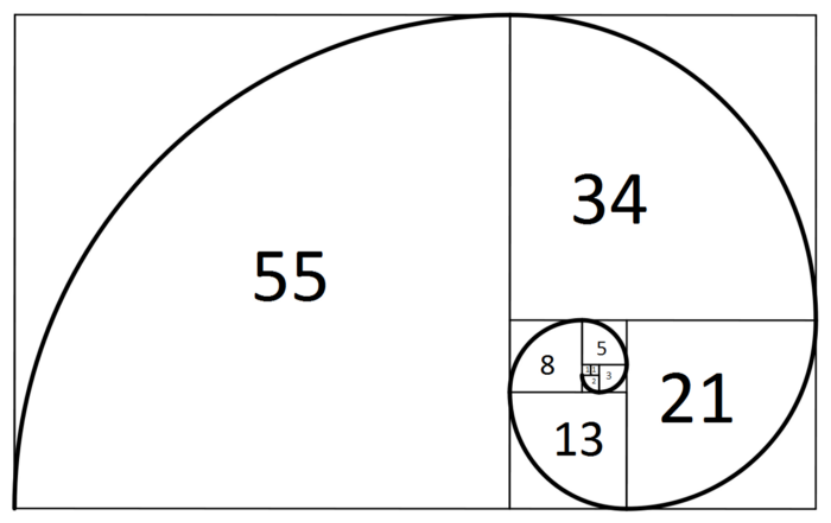
斐波那契图。

5. 数字23

许多人都看过这样的一部电影：金•凯瑞主演的《数字23》。主人公怀尔特自从读过一本带有数字23的书，他似乎就被数字23缠上了。奇怪的是这个数字和他生活中很多事情似乎有神秘联系，这似乎是通灵的完美例子。下面列表中还有很多有趣的蕴含23的东西。：

• 当写下9\11恐怖袭击的完整日期并对他们进行求和我们会发现： 9 + 11 + 2 + 0 + 0 + 1 = 23。当然，也可以这样： 9 + 11 + 2001 = 2021。
• 根据生日悖论，如果要让有至少两个人生日相同的概率大于50%，参加生日宴会的总人数至少要有23个。顺便提一下，如果总共有70个人概率就会高达99%。
• 威廉•莎士比亚诞辰为4月23日，巧合的是，他的忌日也在4月23日。当然，这一天到底是否是他的生日并非十分确定（他是在26日接受洗礼的），但大家都是这么认为的。
• 泰坦尼克号是在1912年4月15日沉没的，把年月日全部加和就会有4 + 1 + 5 + 1 + 9 + 1 + 2 = 23。当然，这有点投机取巧，因为这些日子是被精挑细选的满足规律的日期，很多不满足这个规律的日子都被剔除了。
• 地球相对于它的轨道面倾斜角是23.5°。对了，还可以把23看成2+3。当然也可以说地球的轴倾角是66.5°不过这听上去就没有那么酷了。
• 阿雷西博信号中包含1679字节，分布在73行之中，每一行有23个字节。这是被人类文明制造的，但看上去还是蛮有趣。阿雷西博信号是从地球发射往太空用来探明智慧生命的。它象征着生命。
• 人类有23对染色体。
• 前23个质数的和等于874，874可以被23整除。感谢维基百科提供参考。
• 广岛核弹是在 8:15投掷的。 悲惨的是这次灾难毁灭了几千万人的生命。另外, 8 + 15 = 23.
• 23是包含连续数字的最小质数。
• 圣殿骑士团有23个大头颅大师。
• 人的血液平均每23秒就在身体循环一次。
• 最后，数字23是这个名单上第五个数，也就是第2+3个数，尽管这是我刻意而为的。其实我最后真正想说的是，虽然数字有它独特的魅力，但并非每个数字背后都有神秘元素起作用。我想23就是个很典型的被夸大神秘性的例子。不过在我们所列举的这些数字中，还是有很多有趣的特征的。

4. π和τ

无理数中最著名的无疑是圆的周长与直径之比，也就是常说的圆周率，恐怕没有人没见过这个数。

如果画一个直径为1的圆，它的周长就等于 3.14159…我们把这个无限不循环小数用字母π表示，简单点说就是圆周率。不过不用管这个中学时期的概念，来看看下面这两个有关π的有趣的事实：

• 它的小数部分是无限不循环的。
• 我们都知道π的近似值是22/7，但我们没法给出一个分数精准的描述π，因为它是一个无理数。

那么为什么还要提Tau呢？一些数学家支持用Tau来代替2π，因为这样更便于计算与圆有关的问题。当深挖这些问题时，不得不承认，他们的直觉是对的，可是有谁不爱π呢？

每年的3月的14日被定为π节，因为美国日期写法是月/日，所以就写作3/14。

3. 欧拉的证明

这就是为什么我在标题中用了"美"这个词。难以想象，数学中一些最美丽的概念，竟然可以组合成这么简洁的结果。先来回顾一下我们之前提到的的概念，以及如何运用它们：

• 欧拉 e。
• 虚数单位 i。
• 圆周率 π

最令人惊讶的是这三个数就可以组合成下面这个方程并仅仅得出-1这个简单的结果。

 

 

 

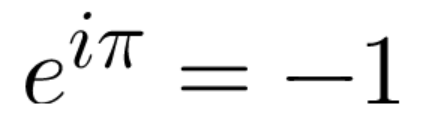
[图片来源于mathsisfun.com]

怎么从这三个小卒得到-1的呢？

正如你所看到的那样，i拥有了把2变成-1的力量。莱昂哈德 · 欧拉对下面我所给出的方程应用了泰勒展开（这里就不详细描述了，因为它们超出了本文讨论的范围）。

 

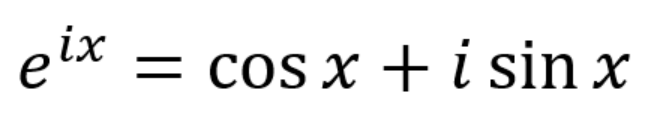
把上面的欧拉公式放在复平面上（以实数轴和虚数轴建立坐标系），就会得到一个圆。如果引入一个半径r，可以把点转换为另一种形式，即r等于e的ix次方。

如果令 x = π, 我们就会得到如下方程：

 

了解到 cos π = -1以及sin π = 0, 右边就会出现i：

 

 

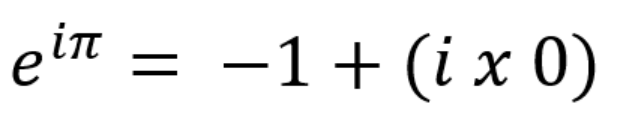
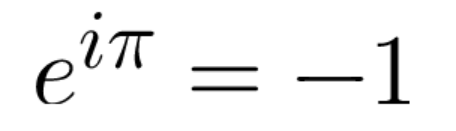
 还可以通过使用新的一个数字来让方程变得更漂亮一点：

 

 

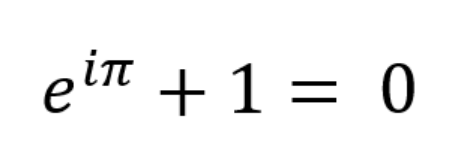
2.数 6174

就像众所周知的卡普雷卡尔常数一样，这个数有很有趣的特点。如果你按下面的方式对它操作，你会得到很神奇的结果。（以下这段文字很多地方都有记录，不过在这里取自维基百科）：

• 取任意一个至少有2位数不同的四位数。
• 分别把这个四位数按升序和降序的方式重新排列，会得到两个新的两位数。
• 现在用这两个数中较大的数减较小的数。
• 重复第二步。

如果你循环的次数足够多，你最后就会得到6174，这就是神奇之处的。为什么无论选什么数字，都会得到6174呢？先用2714做个实验看看吧：

• 7421 -1247 = 6174

再拿3678试一试：

• 8763 -3678 = 5085;
• 8550 -0558 = 7992;
• 9972 -2799 = 7173;
• 7731 -1377 = 6354;
• 6543 -3456 = 3087;
• 8730 -0378 = 8352;
• 8532 -2358 = 6174

如果得到了6174，对它再进行相同的处理，结果仍然是6174因为7641 -1467 = 6174。

这就是我们常说的哈沙德数，也被称为尼云数，是指能够被其各个数位上的数字之和整除的自然数：例如6174 / (6 + 1 + 7 + 4) = 6174 / 18 = 343。 这个名字为6174的有趣添了一笔神秘色彩。

1.黄金比例

我们之前已经讨论过这个比例，但这可能是世界上最为重要的比例。它的名字是黄金比例，以下是它的一些有趣的特征：

• 0.618的倒数是极简的1+0.618，因此， 1 / ϕ ≈ 1 + ϕ
• 它在自然界中广泛存在（就像前面提到的那样）。有些树的生长就是很好的例子，树干先是自由向上生长，长着长着它拥有了一个分叉，于是产生了2个新的起点，其中一个起点会长出2个新的分叉起点，而另一个则不会。这个模式这个规律就好像是斐波那契数列一样。

 

 

 

来源: https://in.pinterest.com/pin/415034921892322849/

• 黄金比例被看作是美的象征，尽管这并没有被证明，但了解这种定义是如何让我们感觉到美这个过程很有趣。拿美人举个例子：根据施密德博士的研究，如果把人的容貌用10分制（尽管这并不一定是最合适的方式）打分，美人的分数为10分，那么普通人的分数就集中在4分到6分之间。美人的打分是这样得出的：首先测量出人脸的长和宽，然后用长度比宽度，最后发现最佳结果为1.618。这意味着美人的脸长度约为1.618倍于它的宽。之后我们再测量其他的部分，例如鼻子到下巴底部的部分，最后再进行对比，以检查是否含有更多美人比例。施密德博士说在完美脸型上耳朵的长度应该等于鼻子的长度，其他特征也是类似。
• 我们的手臂与整个手的比例等于 ϕ。
• 黄金比例广泛存在于几何学中，许多建筑和艺术品中都含有黄金比例。希腊的巴特农神庙就是典型的例子。
• 五角星内部也暗含着黄金比例。

存在的最大数字实际上是40。以下是这个冷笑话的证据：

 

 

消息来源： vsauce.